
# The Oxford Handbook of
## EEG
## FREQUENCY
# T h e Ox for d H a n db o ok of
# **EEG FREQUENCY**
## OXFORD LIBR ARY OF PSYCHOLOGY
*The Oxford Handbook of Internet Psychology* Edited by Adam Joinson, Katelyn McKenna, Tom Postmes, and Ulf-Dietrich Reips
*The Oxford Handbook of Job Loss and Job Search*
Edited by Ute-Christine Klehe and Edwin van Hooft
*The Oxford Handbook of Parenting and Moral Development*
Edited by Deborah J. Laible, Gustavo Carlo, Laura M. Padilla Walker
*The Oxford Handbook of Stigma, Discrimination, and Health* Edited by Brenda Major,
John F. Dovidio, and Bruce G. Link
*The Oxford Handbook of Deaf Studies in Learning and Cognition* Edited by Marc Marschark and Harry Knoors
*The Oxford Handbook of 4E Cognition* Edited by Albert Newen, Leon De Bruin, and Shaun Gallagher
*The Oxford Handbook of Attention* Edited by Anna C. Nobre and Sabine Kastner
*The Oxford Handbook of Clinical Child and Adolescent Psychology* Edited by Thomas H. Ollendick, Susan W. White, and Bradley A. White
*The Oxford Handbook of Group Creativity and Innovation*
Edited by Paul B. Paulus and Bernard A. Nijstad
*The Oxford Handbook of Organizational Citizenship Behavior*
Edited by Philip M. Podsakoff, Scott B. MacKenzie, and Nathan P. Podsakoff
*The Oxford Handbook of Digital Technologies and Mental Health* Edited by Marc N. Potenza, Kyle Faust, David Faust
*The Oxford Handbook of Sexual and Gender Minority Mental Health* Edited by Esther D. Rothblum
*The Oxford Handbook of Psychological Situations*
Edited by John F. Rauthmann, Ryne Sherman, David C. Funder
*The Oxford Handbook of Human Motivation, 2e*
Edited by Richard Ryan
*The Oxford Handbook of Integrative Health Science*
Edited by Carol D. Ryff and Robert F. Krueger
*The Oxford Handbook of Positive Psychology, 3e*
Edited by C.R. Snyder, Shane J. Lopez, Lisa M. Edwards, Susana C. Marques
*The Oxford Handbook of Dialectical Behaviour Therapy*
Edited by Michaela A. Swales *The Oxford Handbook of Music and*
*the Brain* Edited by Michael H. Thaut and Donald A. Hodges
*The Oxford Handbook of Expertise* Edited by Paul Ward, Jan Maarten Schraagen, Julie Gore, and Emilie M. Roth
*The Oxford Handbook of Singing* Edited by Graham F. Welch, David M. Howard, and John Nix
*The Oxford Handbook of Evolutionary Psychology and Behavioral Endocrinology* Edited by Lisa L. M. Welling and Todd K. Shackelford
*The Oxford Handbook of Autism and Co-Occurring Psychiatric Conditions* Edited by Susan W. White, Brenna B. Maddox, Carla A. Mazefsky
*The Oxford Handbook of Adolescent Substance Abuse*
Edited by Robert A. Zucker and Sandra A. Brown
# The Oxford Handbook of
# **EEG FREQUENCY**
*Edited by*
PHILIP GABLE, MATTHEW MILLER, EDWARD BERNAT


### Great Clarendon Street, Oxford, OX2 6DP, United Kingdom
Oxford University Press is a department of the University of Oxford. It furthers the University's objective of excellence in research, scholarship, and education by publishing worldwide. Oxford is a registered trade mark of Oxford University Press in the UK and in certain other countries
© Oxford University Press 2022
The moral rights of the authors have been asserted
First Edition published in 2022 Impression: 1
All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, without the prior permission in writing of Oxford University Press, or as expressly permitted by law, by licence or under terms agreed with the appropriate reprographics rights organization. Enquiries concerning reproduction outside the scope of the above should be sent to the Rights Department, Oxford University Press, at the address above
> You must not circulate this work in any other form and you must impose this same condition on any acquirer
Published in the United States of America by Oxford University Press 198 Madison Avenue, New York, NY 10016, United States of America
> British Library Cataloguing in Publication Data Data available
CIP data is on file at the Library of Congress
ISBN 978–0–19–289834–0
DOI: 10.1093/oxfordhb/9780192898340.001.0001
Printed and bound by CPI Group (UK) Ltd, Croydon, CR0 4YY
Oxford University Press makes no representation, express or implied, that the drug dosages in this book are correct. Readers must therefore always check the product information and clinical procedures with the most up-to-date published product information and data sheets provided by the manufacturers and the most recent codes of conduct and safety regulations. The authors and the publishers do not accept responsibility or legal liability for any errors in the text or for the misuse or misapplication of material in this work. Except where otherwise stated, drug dosages and recommendations are for the non-pregnant adult who is not breast-feeding
Links to third party websites are provided by Oxford in good faith and for information only. Oxford disclaims any responsibility for the materials contained in any third party website referenced in this work.
## Contents
| List of Contributors | ix |
|----------------------------------------------------------------------------------------------------------------------------------------------------------------------------|------|
| Foreword | xiii |
| Preface | xv |
| PART I | |
| 1. Introduction: Methods for Collecting EEG Data for Frequency
Analyses in Humans
Philip A. Gable and Matthew W. Miller | 3 |
| 2. Logic behind EEG Frequency Analysis: Basic Electricity and
Assumptions
Kyle J. Curham and John J. B. Allen | 15 |
| 3. From Neural Oscillations to Cognitive Processes
Andreas Keil and Nina Thigpen | 40 |
| 4. Time-Frequency Decomposition Methods for Event-Related
Potential Analysis
Selin Aviyente | 65 |
| 5. Time Frequency Analyses in Event-Related Potential
Methodologies
Anna Weinberg, Paige Ethridge,
Belel Ait Oumeziane, and Dan Foti | 88 |
| 6. The Relationship Between Evoked and Induced EEG/MEG
Changes: Going Beyond Labels
Ali Mazaheri | 115 |
| 7. Frequency Analysis of the Monkey Neocortical Local
Field Potential
Steven L. Bressler | 131 |
| 8. Gamma Activity in Sensory and Cognitive Processing
DANIEL STRÜBER AND CHRISTOPH S. HERRMANN | 145 |
| 9. Frontal Midline Theta as a Model Specimen of Cortical Theta
JAMES F. CAVANAGH AND MICHAEL X COHEN | 178 |
| 10. The Role of Alpha and Beta Oscillations in the Human EEG during
Perception and Memory Processes
SEBASTIAN MICHELMANN, BENJAMIN GRIFFITHS,
AND SIMON HANSLMAYR | 202 |
| 11. Theory and Research on Asymmetric Frontal Cortical Activity as
Assessed by EEG Frequency Analyses
EDDIE HARMON-JONES, TAYLOR POPP, AND PHILIP A. GABLE | 220 |
| 12. Oscillatory Activity in Sensorimotor Function
BERNADETTE C. M. VAN WIJK | 259 |
| PART III | |
| 13. EEG Frequency Development across Infancy and Childhood
KIMBERLY CUEVAS AND MARTHA ANN BELL | 293 |
| 14. Developmental Research on Time-Frequency Activity in
Adolescence and Early Adulthood
STEPHEN M. MALONE, JEREMY HARPER, AND WILLIAM G. IACONO | 324 |
| 15. Theta-Beta Power Ratio: An Electrophysiological Signature of
Motivation, Attention and Cognitive Control
DENNIS J. L. G. SCHUTTER AND J. LEON KENEMANS | 352 |
| 16. Cortical Source Localization in EEG Frequency Analysis
WANZE XIE AND JOHN E. RICHARDS | 377 |
| 17. Frequency Characteristics of Sleep
ALPÁR S. LÁZÁR, ZSOLT I. LÁZÁR, AND RÓBERT BÓDIZS | 401 |
| 18. A Review of Oscillatory Brain Dynamics in Schizophrenia
KEVIN M. SPENCER | 434 |
| 19. EEG Frequency Techniques for Imaging Control Functions
in Anxiety
JASON S. MOSER, COURTNEY LOUIS, LILIANNE GLOE,
STEFANIE RUSSMAN BLOCK, AND SPENCER FIX | 464 |
| PART IV | |
vi Contents
### **PART II**
Contents vii
| PART IV | | |
|-------------------------------------------------------------------------------------------------------------------------------------------------------|-----|-----|
| 20. Bivariate Functional Connectivity Measures for Within- and
Cross-Frequency Coupling of Neuronal Oscillations
J. MATIAS PALVA AND SATU PALVA | 495 | |
| 21. Multivariate Methods for Functional Connectivity Analysis
SELIN AVIYENTE | 514 | |
| 22. Brain Stimulation Approaches to Investigate EEG Oscillations
FLORIAN H. KASTEN AND CHRISTOPH S. HERRMANN | 532 | |
| 23. Parameterizing Neural Field Potential Data
BRADLEY VOYTEK | 563 | |
| Index | | 579 |
## [List of Contributors](#page-5-0)
**John J. B. Allen**, Distinguished Professor of Psychology, Department of Psychology, University of Arizona, Tucson, AZ
**Selin Aviyente**, Professor, Department of Electrical and Computer Engineering, Michigan State University, East Lansing, MI
**Martha Ann Bell**, University Distinguished Professor, Department of Psychology, Virginia Tech, Blacksburg, VA
**Róbert Bódizs**, Senior Research Fellow, Semmelweis University, Institute of Behavioural Sciences, Budapest, Hungary
**Steven L. Bressler**, Professor, Center for Complex Systems and Brain Sciences, Department of Psychology, Florida Atlantic University, Boca Raton, FL
**James F. Cavanagh**, Associate Professor, Department of Psychology, University of New Mexico, Albuquerque, NM
**Michael X Cohen**, Assistant Professor, Donders Centre for Neuroscience & Radboud University Medical Center, Nijmegen, Netherlands
**Kimberly Cuevas**, Associate Professor, Department of Psychological Sciences, University of Connecticut, Storrs, CT
**Kyle J. Curham**, Department of Psychology, University of Arizona, Tucson, AZ
**Paige Ethridge**, Department of Psychology, McGill University, Montreal, QC, Canada
**Spencer Fix**, Department of Psychology, University of Maryland College Park, College Park, MD
**Dan Foti**, Associate Professor, Department of Psychological Sciences, Purdue University, West Lafayette, IN
**Philip A. Gable**, Associate Professor of Psychology, Department of Psychological and Brain Sciences, University of Delaware, Newark, DE
**Lilianne Gloe**, Department of Psychology, College of Social Science, Michigan State University, East Lansing, MI
**Benjamin Griffiths**, School of Psychology, University of Birmingham, Edgbaston, Birmingham, UK
x LIST OF CONTRIBUTORS
**Simon Hanslmayr**, Professor, Centre for Cognitive Neuroimaging, School for Neuroscience and Psychology, University of Glasgow, UK
**Eddie Harmon-Jones**, Professor, School of Psychological Science, University of New South Wales, Sydney, Australia
**Jeremy Harper**, Department of Psychiatry and Behavioral Sciences, University of Minnesota, Minneapolis, MN
**Christoph S. Herrmann**, Professor, Experimental Psychology Lab, Carl von Ossietzky University, Oldenburg, Germany
**William G. Iacono**, Professor, Department of Psychology, University of Minnesota, Minneapolis, MN
**Florian H. Kasten**, Experimental Psychology Lab, Carl von Ossietzky University, Oldenburg, Germany
**Andreas Keil**, Professor of Psychology, Department of Psychology and Center for the Study of Emotion & Attention, University of Florida, Gainesville, FL.
**J. Leon Kenemans**, Professor, Biopsychology and Psychopharmacology, Utrecht University, Utrecht, Netherlands
**Alpár S. Lázár**, Associate Professor, School of Health Sciences, University of East Anglia, Norwich, UK
**Zsolt I. Lázár**, Assistant Professor, Faculty of Physics, Babeş-Bolyai University, Cluj-Napoca, Romania
**Courtney Louis**, Department of Psychology, College of Social Science, Michigan State University, East Lansing, MI
**Stephen M. Malone**, Research Assistant Professor and Co-investigator, Minnesota Center for Twin & Family Research, University of Minnesota, Minneapolis, MN
**Ali Mazaheri**, Associate Professor, School of Psychology, University of Birmingham, Edgbaston, Birmingham, UK
**Sebastian Michelmann**, Princeton Neuroscience Institute, Princeton, NJ
**Matthew W. Miller**, Associate Professor, School of Kinesiology, Auburn University, Auburn, AL
**Jason Moser**, Professor, Department of Psychology College of Social Science, Psychology, Michigan State University, East Lansing, MI
**Belel Ait Oumeziane**, Department of Psychological Sciences, Purdue University, West Lafayette, IN
LIST OF CONTRIBUTORS xi
**J. Matias Palva**, Research Director, Department of Neuroscience and Biomedical Engineering, Aalto University, Helsinki
**Satu Palva**, Professor, Centre for Cognitive Neuroimaging, School of Psychology and Neuroscience, University of Glasgow, Glasgow
**Taylor Popp**, Carnegie Mellon University, Pittsburgh, PA
**John E. Richards**, Professor, Department of Psychology, University of South Carolina, Columbia, SC
**Stefanie Russman Block**, Department of Psychology, College of Social Science, Michigan State University, East Lansing, MI
**Dennis J. L. G. Schutter**, Professor, Experimental Biopsychology of Motivation and Emotion, Utrecht University, Utrecht, Netherlands
**Kevin M. Spencer**, Research Health Scientist, Veterans Affairs Boston Healthcare System; and Associate Professor of Psychiatry, Harvard Medical School, Boston, MA
**Daniel Str**ü**ber**, Adjunct Professor, Experimental Psychology Lab, Carl von Ossietzky University, Oldenburg, Germany
**Nina Thigpen**, Research Scientist at Google X, The Moonshot Factory, Mountain View, CA.
**Bernadette C. M. Van Wijk**, Marie Curie Research Fellow at the University of Amsterdam, Amsterdam, Netherlands
**Bradley Voytek**, Associate Professor, Department of Cognitive Science, UC San Diego, San Diego, CA
**Anna Weinberg**, Assistant Professor, Department of Psychology, McGill University, Montreal, QC, Canada
**Wanze Xie**, Assistant Professor, School of Psychological and Cognitive Sciences, Peking University, Beijing, China
## [Foreword](#page-5-1)
### Steven J. Luck
When Hans Berger conducted his pioneering human EEG recordings in the 1920s, his first major discovery was the *alpha rhythm*, a 10-Hz oscillation that grew larger when the subject's eyes were closed. A few years later, Lord Adrian (my intellectual great-greatgrandfather) showed that the alpha rhythm also varied according to whether the subject was focusing intensely or daydreaming. Thus the study of EEG oscillations was born.
But this area of research underwent a protracted childhood, because the scientists of the mid-twentieth century could not easily see smaller oscillations amidst the chaotic twists and turns of the scalp EEG. To pull out specific neural processes from the complex and noisy EEG, they began to use signal averaging techniques that can isolate the brain potentials that are triggered by specific events such as the onset of a light (the *event-related potentials* or ERPs). However, these techniques assume that the phase of the signal is constant across trials, and the application of signal averaging to EEG data eliminates or hopelessly distorts oscillating activity. Indeed, for the first 30 years of my own research career, I viewed the alpha rhythm as a nuisance that should be suppressed lest it contaminate my precious ERP waveforms.
All of this began to change in the 1980s and 1990s, partly driven by high-profile studies of local field potential oscillations in animals and partly driven by the application of time-frequency analysis methods to human EEG recordings. The brain oscillations that were obscured by signal averaging could now be visualized and quantified. A new generation of researchers began studying human EEG oscillations and linking them with microelectrode data from animals and computational models of brain dynamics.
In science, the introduction of a new approach often leads to a burst of progress followed by the realization that things are not as simple as they seem. The new wave of oscillation research followed this common path, with the discovery of important new phenomena being accompanied by conceptual and methodological challenges. One such challenge—related to the famous Heisenberg Uncertainty Principle—is that precision in the time-domain is inversely related to precision in the frequency domain. The more precisely you determine the frequency of an oscillation, the less you can say about when the oscillation was present.
A second important challenge is the difficulty of distinguishing between bona fide oscillations and other kinds of neural events. Part of the genius of the Fourier transform xiv Foreword
is that *any* waveform—whether or not it contains oscillations—can be reconstructed by summing together a set of sinusoids. As a result, when you apply a method such as the Fourier transform to a time-domain signal such as the EEG, you will always see activity at some frequencies, whether or not the signal is actually oscillating. And what if the brain is oscillating, but not in a sinusoidal manner? This can lead to completely artifactual results, such as the apparent coupling of the amplitude of one frequency with the phase of another frequency.
A third key challenge is the interpretation of brain oscillations. Virtually any system containing multiple interconnected parts will oscillate when energy is introduced. Those oscillations can be essential to the function of the system, as when the sound of a single violin fills a concert hall or when a clock keeps perfect time. But oscillations can also be a sign of trouble, as when a bridge shakes violently following an earthquake or when a seizure spreads throughout the brain. The fact that the brain oscillates, and that the oscillations vary across states or tasks, does not mean that the oscillations themselves are playing a functional role in the brain's computations. They may be epiphenomenal. Or they may be fundamental. Distinguishing between these possibilities may require invasive recordings in animals or experimental manipulations of oscillations via brain stimulation.
The study of EEG oscillations has reached a key point in its development. The application of time-frequency methods to EEG data is now commonplace, aided by open source data analysis packages such as FieldTrip and EEGLAB. Labs that eschewed these methods for many years—including my own—are now examining oscillations alongside traditional event-related potentials. However, this success means that more researchers are using time-frequency analyses without understanding the challenges involved in properly quantifying and interpreting oscillatory activity. As a result, this edited volume has appeared at the perfect time.
The chapters in this volume will give scientists of all career stages the knowledge they need to understand how oscillations arise in the brain, how they can be accurately quantified, and how they can be appropriately interpreted. I encourage readers to think deeply about the many important issues that are raised in these chapters, especially with regard to the three challenges I have outlined. But if you think deeply and follow the "best practices" described in this volume, you will be able to see brain activity that would otherwise be invisible. And you may make important new discoveries about the human mind and brain.
## [Preface](#page-5-2)
### **Motivation**
The time is ripe for a comprehensive book on the array of historical and cutting-edge frequency and time-frequency approaches to studying EEG/ERP because of the widespread interest in frequency research. There is a great need for a book organizing the diverse and important methods of EEG frequency analyses and interpreting the resultant measures.
One stream of research comes from traditional (band-based) frequency analyses. Likewise, understanding the cutting-edge frequency analyses which may not be familiar to many EEG researchers is increasingly important for investigators applying frequency analyses. However, there is a major need for a comprehensive handbook on analyses within this domain. Although research has been rapidly accumulating over the last decade, there has not been sufficient organization of research on the topic. We believe this comprehensive handbook is increasingly necessary to help delineate the boundaries of the area, the major scientific questions that need to be addressed, and the core theoretical frameworks that can guide future research and development.
Thus, a specific goal of this book is to bring together these various scientific perspectives and research approaches within a single reference volume that provides an integrated, cutting-edge overview of the current state of the field. This volume comprises contributions from leading researchers within various allied disciplines.
The use of electroencephalography (EEG) to study the human mind has seen tremendous growth across a vast array of disciplines due to increased ease of use and affordability of the technology. EEG is a non-invasive measure of electrical brain activity. Typically, researchers investigate the EEG signal using either time-domain (e.g., ERP) analyses or frequency analyses. Several books have examined practicalities of conducting ERP analyses and interpreting various ERP measures. However, a comprehensive book has yet to be developed organizing the numerous ways to process EEG frequency and interpreting frequency measures linked to cognitive, affective, and motor processes.
We (editors Philip, Matt, and Ed) felt a great need for a book organizing the diverse and fascinating methods of EEG frequency analyses and interpreting the resultant measures. Frequency analyses provide unique assessments of neural functioning, neural connectivity, and "resting" neural activity studied by EEG researchers. Further, xvi Preface
frequency-domain measures are reliably associated with cognitive, affective, and motor processes of great interest to neuroscientists and psychological scientists. For example, asymmetrical activation of the frontal cortex as measured by the inverse of alpha-band activity is closely linked with motivation and emotion. In addition, analyses examining the synchrony of EEG frequencies recorded from different scalp locations allow researchers to examine brain connectivity without having to incur the costs of magnetic resonance imaging.
## **ORIGIN**
As EEG frequency researchers, we wanted a resource that introduced the myriad ways in which EEG frequency analyses are being investigated. This volume began while the lead editor, Philip, was on sabbatical and seeking to begin a new chapter in his career. During that time, he visited with Matt Miller and the project quickly developed into a collaborative project. After developing the project more, Matt and Philip brought Ed Bernat on board.
As individual editors, we each had areas of expertise in EEG frequency research, but in developing this volume, we quickly discovered that each of our individual areas of expertise were far different from each other. Three editors were necessary to even try to cover the breadth of EEG frequency research being conducted. In addition, we did not want to create a handbook that focused on EEG frequency research specifically in emotion, cognition, or clinical applications. Instead, we wanted to provide a survey of the breadth of work being conducted with EEG frequency research. Try as we might, we also acknowledge this handbook will inevitably fail to cover everyone's interest across all topics. To that end, we hope to receive feedback from readers so that future editions of this handbook can be expanded to encompass the ever-growing field of EEG frequency research.
Together, the project has been a long labor, but well worth the time and effort to develop the resource. We have been especially excited to work with leading experts in the field as they develop chapters for the volume. We are excited for you as the reader to see what we have gotten to see throughout the editing process: the excitement and development of EEG frequency research across a wide range of fields and programs of research.
## **ORGANIZATION**
To aid in reading the handbook, much thought and structuring has been given to the organization of the chapters. As a whole, the book provides a systematic summary of EEG frequency analyses and applications. Individual chapters give depth to each type Preface xvii
of frequency analysis and interpretation of resultant measures. Chapters are organized into three sections.
The first section of the book is focused on basics of EEG frequency research and linking frequency analyses to other components of EEG research, such as event-related potential (ERP) components and the fundamentals of inference from EEG recording. For the second section, contributors focus on specific EEG frequency components that are commonly studied using traditional frequency bands of activity to study specific psychological processes related to cognition, motivation, and perception. The third section focuses on EEG frequency analyses in special populations and altered states. The fourth section of the handbook concludes with chapters focused on advancing methodology used in EEG frequency research.
The initial chapters in the first section describe methods for collecting EEG data for frequency analyses in humans as well as the basics of electrical activity and assumptions regarding the EEG signal. Following these chapters, contributors consider how the oscillations in the EEG signal may give rise to psychological phenomena, and how ERPs can be decomposed into time-frequency components. The chapters go on to consider the relationships between evoked (ERP-related) and induced EEG activity before shedding light upon frequency analyses of LFPs in non-human primates, which may inform frequency analyses of human EEG. The second section begins with the role of gamma oscillations in cognitive and sensory processing. Then, frontal midline theta, which is often linked to cognitive control, is addressed, followed by the role of alpha and beta oscillations in perception and memory. Next, research on asymmetries in frontal alpha oscillations are linked with motivation, followed by a description of the role of oscillatory activity in sensorimotor function. Moving into the third section of the book, the first chapter in this section focuses on changes in EEG frequency throughout infancy, childhood, adolescence, and early adulthood. Next, follows an examination of the ratio of theta to beta power in motivation and attentional control as they relate to normal and abnormal behavior. Then, the characteristics of the oscillations in persons with schizophrenia are described, followed by an examination of how frequency analyses clarify control processes in people with anxiety. The concluding section of the handbook begins with specialized frequency analyses for source localization and brain connectivity before concluding with chapters describing how to manipulate oscillatory activity with brain stimulation and how to parameterize neural field potential data to, for example, tease apart true oscillations from aperiodic signals.
## **LIMITATIONS OF THE CURRENT VOLUME**
As with any book, the current volume is not a complete work on the topic of EEG frequency analyses. In addition, this is not the first book on EEG frequency research. Many xviii Preface
excellent books have been published this topic. Here we mention what the current book does not include and refer the reader to additional resources available in other books.
One of the most inspiring resources for us as editors is Steven J. Luck and Emily S. Kappenman's *Oxford Handbook on Event-Related Potential Components*. This book has been used in our courses and labs, as well as by countless other EEG researchers. It focuses on the excellent work that has investigated the spectrum of ERP components derived from EEG research. We were inspired to build a similar handbook that would cover EEG frequency analyses. The current book does not address ERP research in much detail. The closest chapters addressing ERP research are Chapters 4 and 5. For those desiring a more comprehensive volume on ERP analyses, please see Luck and Kappenman.
Another extraordinary resource is Mike X. Cohen's *Analyzing Neural Time Series Data: Theory and Practice*. This book has served as the primary resource for many EEG researchers, including us, to learn how to conduct time-frequency analyses, and to teach our students how to perform the analyses. The book is particularly helpful in guiding the reader from the mathematical bases of frequency analyses to the implementation of these analyses in MATLAB. These analyses are referenced throughout our book and include fast Fourier transforms, complex Morlet wavelet convolution, intertrial phase clustering, surface Laplacian filtering, phase- and power-based connectivity measures, and cross-frequency coupling. Chapters in our book that address these "how-to" topics include Chapters 4, 5, 19, 20, 21, and 23.
Finally, Chapter 1 of this volume describes how to collect EEG data. For readers who which to have greater detail about implementing and collect EEG from human participants, we recommend Dickter and Kieffaber's *EEG Methods for the Psychological Sciences*. This book is an excellent resource for researchers beginning to implement EEG.
# Part I
## [Chapter 1](#page-5-3)
# [INTRODUCTION](#page-5-3)
*Methods for Collecting EEG Data for Frequency Analyses in Humans*
PHILIP A. GABLE AND MATTHEW W. MILLER
### **1.1 Chapter Aims**
This chapter aims to provide a structure for readers to understand the methodology behind collecting EEG (electroencephalography) presented in the subsequent chapters. It is important to first understand the research methods involved in recording EEG frequency before delving into more advanced frequency analyses and the interpretations. As researchers, we focus this first chapter on a brief introduction to the topic of EEG methodology and scientific practices. To begin, however, we feel it is important to lay down definitions for terms used throughout the book.
## **1.2 Definitions of EEG Frequency Research**
EEG refers to the recording of electrical brain activity from the human scalp. It is one of the most common methods for measuring brain functioning in areas of mind, brain, and behavior science. EEG data contain rhythmic activity or waves that may reflect neural oscillations, or fluctuations in the excitability of populations of neurons (more on this later). These rhythmic fluctuations are typically described using two main descriptors. The first is frequency, which is the speed of the wave, and it is measured in hertz (Hz), which is the number of wave cycles per second. The second is power, which is the squared amplitude of the wave. The greater the power of an oscillation, the greater the energy of that oscillation. All of the chapters in this work discuss frequency 4 PHILIP A. GABLE and MATTHEW W. MILLER
with most referencing power. Sometimes researchers investigate the phase of the wave, which is the position of the wave measured in radians or degrees. Many of the chapters included here discuss phase.
The brain produces rhythms in multiple frequencies, which can be isolated from the raw EEG signal using multiple techniques described by Curhamn & Allen in Chapter 2, and Voytek in Chapter 23). Different psychological processes are linked to different frequencies, which are often grouped into bands. The most commonly studied bands include delta (1–4 Hz), theta (4–8 Hz), alpha (8–12 Hz), beta (13–30 Hz), and gamma (lower gamma 30–80 Hz; upper gamma 80–150 Hz). While these are not the only frequency bands, these are the bands most typically associated with processes of mind and behavior measured by EEG. Importantly, these bands are not defined without reason, but instead reflect biological changes at the cellular level (see Cohen, 2014 and Buzsaki, 2006 for reviews). However, these bands are not rigid and may vary depending on individual differences, such as brain development, structure, and chemistry. Chapters in the second section of this work note how different frequency bands are associated with cognitive, motivational, and sensorimotor processes.
These definitions are by no means complete. Individual chapters provide more precise definitions of terms used. With this initial framework, readers should be able to venture into subsequent chapters focusing in more detail on these definitions. Because EEG is a rather complex measure, we focus in more detail on the physiological basis and scientific methods used to record and process EEG.
## **1.3 Physiological Basis of EEG**
EEG is measured because all nerve cells communicate using electrical signals, sending information throughout the brain and to the rest of the body. Within a neuron, an action potential is an electrical wave that runs from the axon hillock at the cell body to the axon terminals. At the axon terminals, the action potential causes neurotransmitter to be released. This neurotransmitter crosses the synaptic gap and binds to receptors on the membrane of the postsynaptic cell. Binding to the receptor causes voltage changes by activating ion channels or second messengers that either excite or inhibit the postsynaptic neuron. The summation of this voltage change in the membrane of the dendrites and cell body of the postsynaptic neuron is called a postsynaptic potential. Postsynaptic potentials tend to occur locally, rather than moving down the axon. This allows postsynaptic potentials to summate rather than to cancel, resulting in voltage changes that have larger amplitudes and can be recorded on the cortical surface or at the scalp.
When tens of thousands to millions of neurons are excited or inhibited at the same time, the voltage change outside the cell (extracellular potential) can be recorded at the scalp using EEG, which measures the sum of electrical activity from excitatory and inhibitory postsynaptic potentials over this collection of neurons. The activity can only be recorded on the scalp surface because tissue (cerebrospinal fluid, meninges, skull, and INTRODUCTION 5
skin) between the neurons and scalp conducts the electrical signal. In addition, for electrical activity to be projected to the scalp, cellular alignment must be precisely arranged in parallel so that their effects cumulate to project the electrical activity to the scalp (see Curhamn & Allen, Chapter 2; Keil & Thigpen, Chapter 3). Neurons must be arranged so that the cluster of neurons all have dendrites at one pole and axons departing at the opposite pole. This arrangement is called an open field and occurs when neurons are organized in layers. The cortex, cerebellum, and parts of the thalamus tend to have this open field arrangement of neurons resulting from pyramidal cells.
### **1.4 A Dual Nature**
Due to the electrical basis of the EEG signal, EEG has excellent ability to tell us *when* something is happening in the brain. This is called temporal resolution and is one of the greatest strengths of the EEG signal. The EEG signal measures neural activity at the accuracy of milliseconds, which allows for the ongoing measurement of psychological processes as they unfold (Luck, 2014).
However, the EEG signal is limited in its ability to measure *where* something is occurring. This is called spatial resolution and is one of the greatest weaknesses of the EEG signal. Depending on where the source of the EEG signal is generated, the orientation of the open field neurons might not be parallel to the scalp, thus generating EEG signals in multiple directions. In addition, resistors (e.g., the skull) in the tissue between the neurons and scalp can cause the EEG signal to spread out. Because of the volume conduction through the head, as well as the orientation of the pyramidal cells emitting the signal, the spatial location of the signal is difficult to ascertain. As Keil and Thigpen (Chapter 3) note, a difference in frequency power between two experimental conditions could be the result of a different number of neurons activated, the temporal order in which they were activated, or neurons with different orientations being activated. To address EEG's limited spatial resolution, cortical source localization techniques have been developed and are reviewed by Xie and Richards (Chapter 19). In sum, using an analogy from Steve Luck's ERP Boot Camp, the EEG signal is like being able to see every frame of a movie as it unfolds. However, because of the low spatial resolution, the movie appears a bit blurry.
### **1.5 EEG Equipment and Recording**
The earliest method of EEG measurement was implemented by Hans Berger in the late 1920s. In his early experiments, he used two sponges soaked in saline connected to an amplifier (Berger, 1929). While the equipment and processing of EEG signal has advanced considerably since that time, the basic components remain similar. EEG 6 PHILIP A. GABLE and MATTHEW W. MILLER
electrodes are placed on or near the head, the signal from the electrode is transmitted to an amplifier, and the signal is digitized and recorded.
In psychological research labs, EEG is usually recorded from 32, 64, 128, or more electrodes. In other research (e.g., sleep, nonhuman) fewer electrodes (2–8 electrodes) is more typical. When larger numbers of electrodes are used, electrodes are mounted in an electrode cap or net. When fewer electrodes are used, electrodes may be positioned individually on the head using a bonding agent. Electrodes can either be wet electrodes or dry electrodes. Wet electrodes are made of silver, silver-chloride, or tin, and a conductive gel or liquid is placed inside or around the electrode. Dry electrode systems use electrodes coated in gold, silver, or nickel, and place electrodes directly on the scalp without a conductive medium. Wet electrodes generally have higher signal quality, but dry electrodes may be preferred when high impedance levels are tolerable, or when recording for long periods.
Electrode systems will have active or passive electrodes. Active electrodes contain a small pre-amplification unit directly attached to the conductive metal in the electrode. This allows the EEG signal picked up at the sensor to be immediately amplified before additional environmental noise can be introduced. Passive electrodes do not have amplification at the electrode, and instead carry the signal to an amplifier about a meter away. Compared to passive electrodes, active electrodes minimize noise introduced during signal transmission, tolerate high impedance recording, and reduce participant preparation time. Passive electrodes have a lower profile to benefit transcranial magnetic stimulation over the cap and can be used inside an MRI bore.
Electrode placement is predominantly based on the 10–20 system (Jasper, 1958). Electrodes are named using the first letter to refer to the brain region under the electrode from anterior to posterior (e.g., Fp—frontal pole, F—frontal, C—central, P—parietal, T—temporal, O—occipital). Numbers following the letter are used to indicate the lateral position of the electrodes. Ascending odd numbers indicate sites more lateral over the left hemisphere of the brain, whereas ascending even numbers indicate sites more lateral over the right hemisphere of the brain. The letter Z is used to designate medial sites. In addition to the recording electrodes, EEG also requires a ground electrode, which assists in reducing electrical noise, as well as a reference electrode placed on the head or face.
The raw EEG signal is usually filtered during recording. Signals below 0.1 Hz or above 200 Hz are removed because the frequency bands of interest fall within this range. A filter at 60 Hz (in North and South America) or 50 Hz (in Europe, Asia, and Africa) may also be used to further reduce electrical noise from alternating current.
### **1.6 Artifacts**
The quality of the EEG is crucial to EEG frequency analysis. To best record EEG signal reflecting brain activity, researchers must remove signal that occurs because of anything other than neural activity. Signal that is not naturally present is called artifact. These INTRODUCTION 7
can be biological (e.g., muscle movement) or nonbiological (e.g., electrical noise). Much artifact can by eliminated by taking preventative measures. Artifact that cannot be prevented should be removed.
Muscle artifact, or electromyography (EMG), is one of the most common types of artifacts and is usually high in frequency (100–500 Hz). Usually, this falls outside of the frequency range typically investigated by researchers. However, some muscle artifact may seep into lower frequencies. Researchers can reduce muscle artifact by instructing participants to limit their muscle movements. Muscle artifact that does occur can be removed through visual inspection, filtering, and automatic artifact detection algorithm. It should be noted that some muscle artifact may be related to the experiment (e.g., sensorimotor studies). In such cases, it may be beneficial to measure EMG at the site movement is expected (e.g., the hand), then control for it in analyses.
Eye movements are another common type of artifact. The eyeball is polarized which causes large artifact in the form of voltage changes resulting from moving the eyes. Like dealing with muscle artifact, eye movement artifact can be removed from signal using recordings near the eyes called electro-oculograms (EOG). One pair of EOG electrodes are placed above and below the eye, while another pair is placed just lateral to either eye on the temple. Eye blinks also create eye movement artifact. It is preferable to correct blink artifact using an artifact reduction algorithm based on regression, principal component analyses, or independent component analyses.
Artifacts occurring in the environment are the result of nonbiological factors. The most common sources of these artifacts are the result of external electrical noise coming from compact fluorescent lightbulbs, data hubs, or electrical junctions. Grounding will aid in reducing these sources of noise, as will electromagnetically shielded rooms.
### **1.7 Frequency Processing**
Once an EEG signal is recorded, the raw data must go through several processing steps before it is in a format useable in analyses. The raw signal is collected in the time-domain but must be converted into a frequency-domain representation. One way this can be accomplished is in the form of a power spectrum, which collapses frequency data across time to map the frequencies present. A frequency analysis can be conducted over windows that are minutes, seconds, or milliseconds in length; these are called epochs. Epochs that are seconds or minutes can be analyzed for power spectra using a Fourier transform, which decomposes a signal into a series of sine and cosine functions of various frequencies. The function of each frequency begins with its own phase. A Fourier transformation assumes that the epoch repeats infinitely forward and infinitely backward in time. A process called windowing is used to prevent artifact created from the Fourier transform. However, windowing can also introduce artifact and data loss into the frequency analysis. Overlapping epochs is a way to prevent discontinuity, data loss near the ends of the epoch, and to help meet the assumptions of the Fourier transform in windowing.
8 PHILIP A. GABLE and MATTHEW W. MILLER
One of the most common forms of signal frequency processing is to use a fast Fourier transform (FFT). An FFT provides the spectrum of frequency power for a period, which is often averaged across a range of frequencies comprising a band (e.g., theta). It also provides a spectrum of phase. The power spectrum reflects the energy of each frequency determined by the squared amplitude of the wave. The phase spectrum reflects the phase in radians or degrees of the sine or cosine wave at each interval (e.g., 1/T). Most frequency analyses focus exclusively on frequency power. However, there is increasing interest in examining the phase of frequencies (e.g., see Michelmann, Griffiths, & Hanslmayr, Chapter 10; Palva & Palva, Chapter 20). Crucially, the FFT has two limitations: it poorly depicts changes in the frequency spectrum over time, and it assumes the EEG data are stationary during the period to which the FFT is applied. To overcome these limitations, time-resolved frequency decomposition techniques are growing in popularity, particularly wavelet analyses (e.g., complex Morlet wavelets), which reveal changes in power at various frequencies with excellent temporal precision (see Aviyente, Chapter 4; Weinberg, Ethridge, Oumeziane, & Foti, Chapter 5).
### **1.8 Experimental Design**
Regardless of the EEG recording and processing, researchers need to be considerate of experimental design. In any experiment, researchers should manipulate a single variable at a time to ensure internal reliability, but this procedure is challenging in EEG research. This follows because manipulating one variable between conditions may inadvertently change a second variable between conditions that affects EEG. For example, if an experimental condition attempts to manipulate participants' motivation while they are physically responding to stimuli, then EEG linked to motivation may change (see Harmon-Jones, Popp, & Gable, Chapter 11) but so may the vigor of their responses and EEG linked to sensorimotor function (see van Wijk, Chapter 12). Thus, it is crucial that researchers attempt to experimentally control for such factors in their experimental design or statistically account for them by collecting covariates, such as EMG to index the vigor of motor responses.
#### **1.8.1 Reproducibility in Electrophysiology: Challenges and Recommendations**
A scientific discipline benefits from reproducible results because they strengthen confidence that they reflect the way a system operates under certain conditions.1
1 There have been special issues in the *International Journal of Psychophysiology* and *Psychophysiology* devoted to reproducibility and, relatedly, open science in cognitive electrophysiology, and readers are encouraged to read these special issues (Kappenman & Keil, 2017; Larson & Moser, 2017).
INTRODUCTION 9
We use Goodman, Fanelli, and Ioannidis's (2016) definition of reproducible results as "obtaining the same results from the conduct of an independent study whose procedures are as closely matched to the original experiment as possible" (pp. 2–3). Although there are different definitions of what it means to obtain "the same results" (Open Science Collaboration, 2015), we hope that closely matched studies yield effects with confidence intervals that overlap substantially (for details on using confidence intervals in EEG studies, see Groppe [2017]), thus allowing us to make precise inferences about the true size of the effect being studied. Since reproducible results are crucial for a discipline, it is important to consider what can be done to obtain them. We discuss several research practices that increase the likelihood that an original result will be reproducible and that subsequent studies reproduce the original result, as well as challenges faced by cognitive electrophysiology researchers attempting to do so.
### **1.9 Pre-Register Specific Hypotheses**
Each study should test specific hypotheses because results that confirm hypotheses are more likely to be true than results based on exploratory analyses (Ioannidis, 2005). Thus, it is crucial that researchers do not rewrite their hypotheses to fit with their results, a practice known as HARKing (hypothesizing after results are known), as it exaggerates the confidence the reader has that the results are true. One method to avoid HARKing is pre-registering hypotheses using the Open Science Framework (osf.io), aspredicted. org, or other repositories. However, formulating specific hypotheses for cognitive electrophysiology studies can be difficult, especially if researchers want to frame them statistically. For example, a researcher may be confident in predicting that an experimental condition will affect EEG activity, but they may struggle to define "EEG activity" as a dependent variable. In ERP studies, this is less of a concern because the dependent variables (ERP components) are well-characterized (Kappenman & Luck, 2012); however, there are fewer well-characterized time-frequency variables. Although researchers can be vague about defining their time-frequency variables, they should then use statistical analyses with strict corrections for multiple comparisons (see Cohen, 2014). This reduces the likelihood of making Type I errors, but consequently increases the likelihood of making Type II errors. (Researchers may also consider data-driven region-ofinterest approaches; see Brooks et al., 2017). Therefore, time-frequency analyses will benefit from having well-defined dependent variables (Indeed, this was an initial impetus for this book!).
For example, if a researcher believes an experimental manipulation is likely to influence EEG activity related to cognitive control, they can have a clearly defined dependent variable of oscillatory activity in the theta frequency bandwidth measured from frontal midline electrodes over a certain time (Cavanagh & Cohen, Chapter 9). In a pre-registration, researchers should use a more precise definition of their dependent variable than "frontal 10 PHILIP A. GABLE and MATTHEW W. MILLER
midline theta". For example, they could specify that they will determine the wavelet of 4– 8 Hz that exhibits the greatest peak power between 200 and 600 ms after stimulus onset at electrode Fz for each participant, and then compute the average power of this wavelet during the 200–600 ms time epoch at Fz. They could also introduce some flexibility into the specification of the dependent variable by noting that they will choose a different bandwidth, epoch, and/or electrode if the grand average time-frequency plot (averaged across all conditions) reveals an unexpected time-frequency and/or scalp distribution. In this example, the average across all conditions avoids biasing the analysis in favor of choosing a time-frequency window exhibiting differences between conditions. Besides reducing HARKing and facilitating the specification of dependent variables, pre-registration is crucial for holding researchers accountable to their research design, statistical analyses, and sample size; however, none of these positive features of pre-registration work if researchers deviate from their pre-registration without properly noting the deviation (Claesen et al., 2019).
## **1.10 Increase Power and Conduct A Priori Power Calculations**
Another way that researchers can increase the likelihood that study results are reproducible is by increasing the power of their studies (Ioannidis, 2005). Alarmingly, Button and colleagues' (2013) analysis of neuroscience studies found their average power was very low (8–31%). There are two general ways that researchers can increase the power of their studies. First, researchers should attempt to maximize the effect they are studying and minimize its variance (i.e., increase the standardized effect size). This can be done by using strong experimental manipulations and reliable dependent variables, such as those discussed in this work. Additionally, researchers should increase the signal to noise ratio in their studies by optimizing the number of trials and collecting good EEG data (Cohen, 2017; Luck, 2014).2 Further, when possible, researchers should use within-subjects designs, which is already the case in many cognitive electrophysiology studies. Second, researchers should collect larger samples, which is particularly important when testing between-subjects effects or within-between subject interaction effects. Cognitive electrophysiology studies can require a lot of time to collect and process data, so collecting more participants may seem burdensome, especially for researchers investigating small–medium effects. For example, a two-tailed
2 A good way for researchers to benefit the field (and their citation count) may be for them to establish the number of trials required for different time-frequency variables in different paradigms, which has been done for ERP variables (e.g., Rietdijk et al., 2014). It is worth noting that simply adding more trials may not increase the signal to noise ratio, since participants may fidget more toward the end of long data collections, consequently increasing noise.
INTRODUCTION 11
dependent *t*-test for an effect size of *dz* = 0.35, an alpha = .05, and power = .90 requires 88 participants, according to G\*Power 3.1.9.4 (Faul et al., 2009). Indeed, it is likely that researchers will often find themselves studying small-medium effects. Specifically, when researchers conduct a priori power calculations to determine their sample sizes, they should assume that the effect sizes in the extant literature are inflated, due to publication bias by researchers and journals (i.e., only publishing significant results) (for a more detailed discussion on sample size calculations in EEG studies, see Larson & Carbine, 2017). Although it is difficult to collect and process large samples, it is crucial to the reproducibility of cognitive electrophysiology studies. To reduce the demands large sample sizes impose, researchers who mentor doctoral students, review for and sit on the editorial boards of journals, are involved in hiring decisions about faculty and post-doctoral researchers, and are involved in promotion and tenure decisions should reconsider expectations about the speed of science and the number of publications (for further discussion on these issues, see Bradley (2017) and Yeung [2019]). Also, if a researcher is concerned about allocating a lot of time to a study that may not yield significant results, they can conduct a sequential analysis where they pause data collection after a pre-specified sample has been collected and then determine whether to continue data collection based on if the incremental results are significant (given an adjusted alpha level) and if the incremental results suggest an effect size that is too small to be of interest (Lakens, 2014).
## **1.11 Make Methods, Materials, and Data Open**
In addition to pre-registered hypotheses and adequately powered studies, researchers should also make their methods, materials, and data accessible3 . In so doing, they will allow other researchers to "methodologically reproduce" the original study (Goodman et al., 2016), which should increase the likelihood of observing the same results. Researchers should make their stimuli and stimulus presentation scripts available and include specific details about instructions given to participants and the equipment used for the study. Further, researchers should also make signal and statistical processing scripts available and provide their data when possible so that other researchers can attempt to reproduce analyses or explore new ones. There are various ways to provide this information, including on the Open Science Framework and GitHub (github.com).
3 There is a special issue in the *International Journal of Psychophysiology* devoted to open science in human electrophysiology, and readers are encouraged to read it (Clayson, Keil, & Larson, 2022).
12 PHILIP A. GABLE and MATTHEW W. MILLER
### **1.12 Replicate and Expand**
The recommendations were made to increase the likelihood that researchers' original results will be reproducible, but the recommendations also apply to researchers attempting to reproduce original results. Crucially, researchers attempting to reproduce original results should also attempt to replicate and expand an original finding (Cohen, 2017), preferably increasing the sample size by two and half times the original (Simonsohn, 2015). Specifically, cognitive electrophysiology will benefit if most studies include an attempt to reproduce an original result and then add a new result (e.g., by adding a new experimental condition). With results from replication attempts, more precise estimates about the direction and size of effects can be made. Of course, it is nearly impossible to reproduce a study methodologically. For example, different researchers may have different criteria for manually rejecting trials, and different independent component analyses may yield different components. However, researchers can still come quite close to a methodological reproduction, especially if methods and materials are available for them to use. A challenge for cognitive electrophysiologists is that they often employ different signal processing methods, such as subtracting or not subtracting the ERP from an epoch of EEG data prior to convolving the data with a wavelet. To this end, researchers should use the same methods as the original study, unless a different method is clearly superior. Of course, whether a different method is clearly superior is debatable; thus it is incumbent upon the researcher conducting the methodological reproduction to state their case in a compelling way.
### **1.13 Explore**
Some of the most exciting and reproducible effects in cognitive electrophysiology have been discovered by accident (e.g., Kutas & Federmeier, 2011), meaning that they would not have occurred if researchers had only conducted confirmatory research testing a priori hypotheses. Thus, it is imperative that researchers conduct exploratory analyses in addition to confirmatory analyses. However, results from exploratory analyses should be clearly labeled as such to avoid misleading readers to having excessive confidence in the result. Ideally, then, a study will test pre-registered confirmatory hypotheses that replicate and expand an original result and conduct exploratory analyses. Compelling results from the exploratory analyses can then serve as a priori hypotheses in future confirmatory research. Finally, some of the most exciting exploratory research may come from analyzing old data in new ways. For example, Voytek (Chapter 23) proposes exciting new analytical methods that researchers can apply; his signal processing scripts are freely available [\(https://voyteklab.com/code\)](https://voyteklab.com/code), and researchers can use these scripts to analyze their old data or other openly available data.
INTRODUCTION 13
### **References**
- Berger, H. (1929). Über das Elektrenkephalogramm des Menschen. *Archiv für Psychiatrie und Nervenkrankheiten*, *87*, 527–570. [https://doi.org/10.1007/BF01797193.](https://doi.org/10.1007/BF01797193)
- Bradley, M. M. (2017). The science pendulum: from programmatic to incremental—and back? *Psychophysiology*, *54*, 6–11. doi: 10.1111/psyp.12608
- Brooks, J. L., Zoumpoulaki, A., & Bowman, H. (2017). Data-driven region-of-interest selection without inflating Type I error rate. *Psychophysiology*, *54*, 100–113. doi: 10.1111/psyp.12682
- Buzsáki, G. (2006). *Rhythms of the brain*. Oxford University Press.
- Button, K. S., Ioannidis, J. P. A., Mokrysz, C., Nosek, B. A., Flint, J., Robinson, E. S. J., & Munafò, M. R. (2013). Power failure: Why small sample size undermines the reliability of neuroscience. *Nature Reviews Neuroscience*, *14*, 365–376. doi:10.1038/nrn3475
- Claesen, A., Gomes, S., Tuerlinckx, F., & Vanpaemel, W. (2019). Comparing dream to reality: An assessment of adherence of the first generation of preregistered studies. *PsyArXiv* [online].
- Clayson, P. E., Keil, A., & Larson, M. J. (2022). Open science in human electrophysiology. *International Journal of Psychophysiology*, *174*, 43–46. [https://doi.org/10.1016/j.ijpsy](https://doi.org/10.1016/j.ijpsycho.2022.02.002) [cho.2022.02.002](https://doi.org/10.1016/j.ijpsycho.2022.02.002)
- Cohen, M. X. (2014). *Analyzing neural time series data: Theory and practice*. MIT Press.
- Cohen, M. X. (2017). Rigor and replication in time-frequency analyses of cognitive electrophysiology data. *International Journal of Psychophysiology*, *111*, 80–87. doi: 10.1016/ j.ijpsycho.2016.02.001
- Faul, F., Erdfelder, E., Buchner, A., & Lang, A. (2009). Statistical power analyses using G\*Power 3.1: Tests for correlation and regression analyses. *Behavior Research Methods*, *41*, 1149–1160. doi:10.3758/BRM.41.4.1149
- Goodman, S. N., Fanelli, D., & Ioannidis, J. P. A. (2016). What does research reproducibility mean? *Science Translational Medicine*, *8*, 341ps12. doi: 10.1126/scitranslmed.aaf5027
- Groppe, D. M. (2017). Combatting the scientific decline effect with confidence (intervals). *Psychophysiology*, *54*, 139–145. doi: 10.1111/psyp.12616
- Ioannidis, J. P. A. (2005). Why most published research findings are false. *PLoS Medicine*, *2*, e124. doi: 10.1371/journal.pmed.0020124
- Jasper, H. H. (1958). The ten-twenty electrode system of the International Federation. *Electroencephalography and Clinical Neurophysiology*, *10*, 371–375.
- Kappenman, E. S., & Keil, A. (2017). Introduction to the special issue on recentering science: Replication, robustness, and reproducibility in psychophysiology. *Psychophysiology*, *54*, 3–5. doi: 10.1111/psyp.12787
- Kappenman, E. S., & Luck, S. J. (Eds.) (2012). *The Oxford handbook of event-related potential components*. Oxford University Press.
- Kutas, M. & Federmeier, K. D. (2011). Thirty years and counting: Finding meaning in the N400 component of the event-related brain potential (ERP). *Annual Review of Psychology*, *62*, 621– 647. doi: 10.1146/annurev.psych.093008.131123
- Lakens, D. (2014). Performing high-powered studies efficiently with sequential analyses. *European Journal of Social Psychology*, *44*, 701–710. doi: 10.10002/ejsp.2023
- Larson, M. J. & Carbine, K. A. (2017). Sample size calculations in human electrophysiology (EEG and ERP) studies: A systematic review and recommendations for increased rigor. *International Journal of Psychophysiology*, *111*, 33–41. doi: 10.1016/j.ijpsycho.2016.06.015
14 PHILIP A. GABLE and MATTHEW W. MILLER
- Larson, M. J. & Moser, J. S. (2017). Rigor and replication: Toward improved best practices in human electrophysiology research. *International Journal of Psychophysiology*, *111*, 1–4. doi: 10.1016/j.ijpsycho.2016.12.001
- Luck, S. J. (2014). *An introduction to the event-related potential technique* (2nd ed.). MIT Press. Open Science Collaboration. (2015). Estimating the reproducibility of psychological science. *Science*, *349*, aac4716. doi: 10.1126/science.aac4716
- Rietdijk, W. J., Franken, I. H., & Thurik, A. R. (2014). Internal consistency of event-related potentials associated with cognitive control: N2/P3 and ERN/Pe. *PLoS One*, *17*, e102672. doi: 10.1371/journal.pone.0102672
- Simonsohn, U. (2015). Small telescopes: detectability and the evaluation of replication results. *Psychological Science*, *26*, 559–569.
- Yeung, N. (2019). Forcing PhD students to publish is bad for science. *Nature Human Behaviour*, *3*, 1036. doi: 10.1038/s41562-019-0685-4
# [CHAPTER 2](#page-5-4)
# [LO GIC BEHIND EEG](#page-5-4) [FREQUENCY ANALYSIS](#page-5-4)
*Basic Electricity and Assumptions*
KYLE J. CURHAM AND JOHN J. B. ALLEN
### **2.1 Introduction**
The brain is an electrochemical machine. Although nerve cells differ greatly in their size and morphology, all pass messages using electrical signals, sending information throughout the brain and to the rest of the body via the spinal cord. Within any neuron, an action potential is a wave of electrical activity that travels along the nerve membrane. Action potentials are triggered by the summation of input from other neurons using chemical neurotransmitters, which create voltage potential changes in the post-synaptic neuron. Surface-recorded EEG is blind to the activity of single neurons but can noninvasively measure the electrical activity resulting from summated excitatory and inhibitory post-synaptic potentials over millions of these signals in humans. EEG has excellent temporal resolution, but poor spatial resolution; it can tell us *when* something is happening in the brain, but not precisely *where* it is happening.
EEG gives an incomplete picture of the electrical activity occurring in the brain. The cortex is the outermost layer of the brain, and the primary generator of the electrical activity we measure with EEG. Our ability to detect cortical activity largely depends on the parallel arrangement of cortical pyramidal neurons. When millions of parallel neurons fire simultaneously, their electrical activity adds together to generate a signal large enough to detect at the scalp. However, when neural populations fire incoherently, or when they are not arranged in a parallel formation, the electrical activity does not add constructively, so there is no observed signal at the scalp. This chapter introduces basic concepts in electricity in signal processing, with some practical considerations for data collection and analysis, to help readers understand EEG measurement and interpretation.
16 KYLE J. CURHAM and JOHN J. B. ALLEN
## **2.2 Electricity—Voltage, Current, and Resistance**
Every physical thing is made up of atoms, which in turn are made up of fundamental particles including protons, neutrons, and electrons. Protons have a positive charge, neutrons have a neutral charge, and electrons have a negative charge. Charges of the same sign repel, and opposite charges attract. A few simple experiments demonstrate the existence of electrical charge. For example, rubbing a balloon on a wool sweater makes the balloon negatively charged as electrons move from the wool to the balloon (Figure 2.1). The degree of attraction or repulsion between two point charges is proportional to the product of the charges divided by the inverse squared distance between them. Therefore, when the electron-rich balloon is brought into proximity of the electronpoor wool, or any neutral surface such as a piece of paper or the wall, the balloon will be attracted. If you subsequently rub a second balloon in the same way, the two balloons will repel each other since they are both negatively charged.
Most of the time, atoms have equal numbers of protons and electrons. However, atoms can become *ionized* when electrons are removed or added, resulting in a net charge. *Electricity* is the phenomenon that describes the behavior and movement of charge. In general, it doesn't matter whether it is the electrons or ions that are moving. The flow of charge can be accomplished either by the transfer of electrons from atom to atom, or, in the case of electrophysiology, by the diffusion of charged ions across cellular membranes.
The degree to which electrons are free to move from atom to atom varies by material type. For example, in metals, the outermost electrons are so loosely bound that they freely move in the space between atoms at room temperature. Because these unbound electrons are free to travel from atom to atom, they are called *free electrons*. The relative mobility of electrons within a material is known as electrical *conductivity*. Conductivity is determined by the types of atoms in a material, and how the atoms are linked together with one another. Materials with few or no free electrons are called *insulators*, and materials with many free electrons are called *conductors*. The directed motion of electrons is called electrical *current*. Just like water flowing through a pipe, electrons move within the empty space between atoms. Under normal conditions, the motion of free electrons in a conductor is random, with no particular direction or speed. However, electrons can be influenced to move in a coordinated fashion through a conductive material by supplying a *voltage*. Voltage is the "pressure" that pushes on free electrons to cause them to flow. The ability of a current to flow from one location to another depends on the *resistance*. In insulating materials, such as glass or rubber, electrons have little freedom to move from atom to atom. The less freedom electrons have to move from atom to atom, the greater the resistance to the flow of charge. A conductor's resistance generally increases as its length increases or its diameter decreases. It is again useful to refer to the water analogy: water can flow more easily through a short, wide pipe than a long, narrow pipe. The international system of units (SI) of current is called the *ampere*.
LOGIC BEHIND EEG FREQUENCY ANALYSIS 17

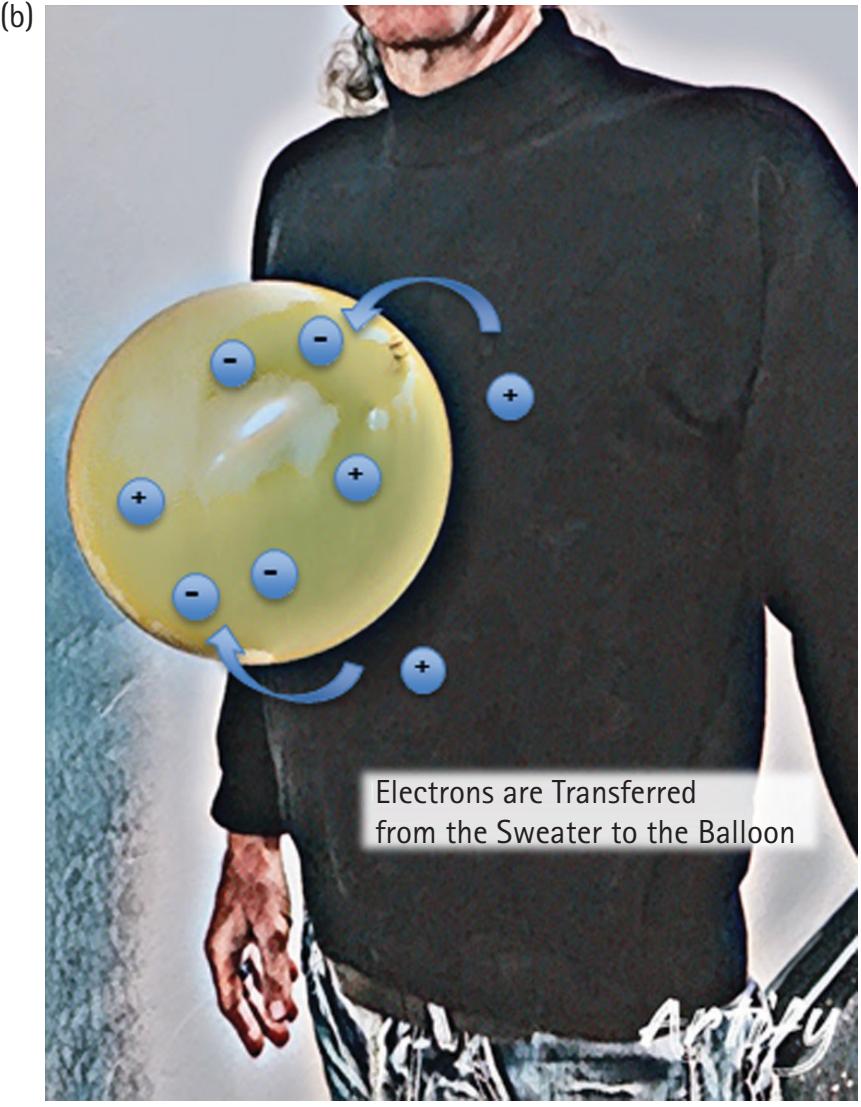
**Figure 2.1** Before rubbing the balloon against the sweater (A), no net accumulation of electrons exists on the balloon. After rubbing the balloon on the sweater (B), the balloon has accumulated an excess of electrons, and the resultant negative charge of the balloon and positive charge of the sweater creates a force of attraction sufficient to keep the balloon from being pulled to the ground by gravity.
Figure credit: K. Ehrmann.
18 KYLE J. CURHAM and JOHN J. B. ALLEN
| Symbol | Term | Definition | Unit |
|--------|-------------|-----------------------------------------------------------|---------------------|
| E | Voltage | Electromotive force | Volts (V) |
| I | Current | Rate of flow | Amperes (A) |
| R | Resistance | Opposition to current | Ohm (Ω) |
| C | Capacitance | Ratio of the change in charge
to the change in voltage | Farad (F) |
| P | Power | Rate of work | Watt (w) |
| W | Energy | Ability to do work | Watt-second (Joule) |
One ampere is defined as one coulomb of charge (or 6 × 1018 electrons) flowing past a given point in a conductor in one second. The *volt* is the unit of pressure, that is, the amount of *electromotive force* (EMF) required to push a current of one ampere through a conductor with a resistance of one ohm, or 1 volt/ampere.
When resistance is high, electrons tend to gather on one side of the insulating material and the positive ions tend to gather on the other, effectively storing *potential energy* in an *electric field*. At some point, the voltage across the material will exceed a threshold known as the dielectric constant, at which point current begins to flow. This tendency for high resistance to result in charge separation is known as *capacitance*. The amount of charge stored in the capacitor is directly proportional to the surface area of the dielectric (the electrical insulator polarized by the electric field) (Table 2.1).
### **2.3 Circuits**
An electrical circuit consists of closed conductive paths between circuit elements. Elements may consist of resistors, capacitors, voltage sources, or current sources. Electrical components may be wired in series or parallel with each other (Figure 2.2). In many cases, circuits consist of some complex combination of series and parallel components. However, these circuits may often be represented by simpler equivalent circuits with identical electrical properties.
To gather some intuition for the flow of current in simple circuits, we refer back to the water analogy. The resistance increases as the pipe gets longer. This is equivalent to stringing together multiple resistors in series. The rule to combine resistors in series is additive:
$$R_{series} = R_1 + R_2 + \ldots + R_n$$
LOGIC BEHIND EEG FREQUENCY ANALYSIS 19

**Figure 2.2** Simple series (left) and parallel (right) circuits. Circuit components labeled with R indicate resistors. Circuit components labeled with V indicate voltage sources.
Conversely, adding multiple resistors in parallel will decrease the overall resistance:
$$\frac{1}{R_{parallel}} = \frac{1}{R_1} + \frac{1}{R_2} + \dots + \frac{1}{R_n}$$
As more "pipes" are added, the water has more paths to escape, decreasing the overall resistance to flow. Capacitors wired in series or parallel follow the same rules, but reversed:
$$\frac{1}{C_{series}} = \frac{1}{C_1} + \frac{1}{C_2} + \dots + \frac{1}{C_n}$$
$$C_{parallel} = C_1 + C_2 + \ldots + C_n$$
Most circuits are some complex combination of series and parallel. We can approach these circuits one piece at a time, deriving a new equivalent circuit at each step (Figure 2.3).
The next few sections explore examples of equivalent circuit representations, and we use equivalent circuit representations to learn the voltages and currents at every point in the original complex circuit. We later show how models of neurons can be represented as a simple equivalent circuit of capacitors, resistors, and voltage sources.
20 KYLE J. CURHAM and JOHN J. B. ALLEN
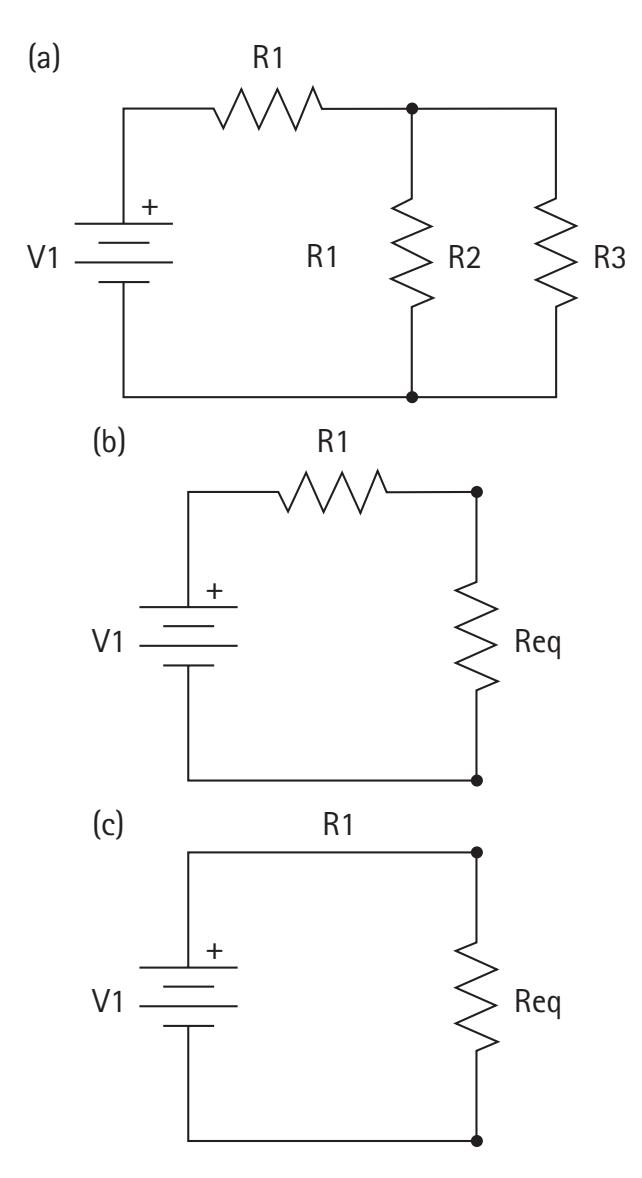
**Figure 2.3** Reducing a complex circuit (left) to a simple equivalent circuit (right). In an intermediate step, we combine parallel resistors 2 and 3 (middle). Next, we combine resistor 1 with the equivalent resistor from the intermediate step.
### **2.4 Direct current**
Circuits come in two basic flavors: direct current (DC) and alternating current (AC). The difference depends on whether the voltage and current change directions over time. DC circuits maintain currents flowing in a constant direction within a closed loop, whereas AC circuits have current that repeatedly reverses direction. A DC electric source feeds from one terminal to a set of circuit elements and then back to the other terminal, in a complete circuit. Figures 2.2 and 2.3 are both DC circuits due to their constant voltage power source. Note some resistors are connected in parallel, while others are connected in series. At each step, we can combine resistors according to the rules in Section 2.3 to derive a simpler equivalent circuit.
Some circuits may contain both resistors and capacitors. These are known as RC circuits. In a simple circuit with one resistor and one capacitor in series, the capacitor must discharge through the resistor. This discharge occurs at an exponential rate determined by the *RC time constant*. The time constant indicates the number of seconds for the capacitor to become 63.2% charged, or, equivalently, the time for current flow LOGIC BEHIND EEG FREQUENCY ANALYSIS 21
to have slowed by 63.2% from its starting value. This choice of time constant has an intuitive explanation: at any moment in time, the rate of change in voltage is equal to the voltage divided the time constant. For example, a 1 mF cap and a 1 kΩ resistor yields a time constant of one second. If the capacitor is charged to 5 volts, the voltage will fall at a rate of 5 V/s. If the capacitor is charged to 2 volts, the voltage will fall at a rate of 2 V/s.
### **2.5 Alternating Current**
In contrast to DC signals, some sources of electricity produce AC, where voltages and currents periodically reverse direction and switch back and forth between positive and negative polarity. The electricity that comes from an American wall outlet is an example of AC. The current in North America is 120 VAC and changes direction 60 times per second. AC circuits can exhibit more interesting behaviors than DC circuits. For example, at low frequencies, a capacitor acts like an open circuit, so no current flows in the dielectric. However, when driven by an AC source, a capacitor will only accumulate a limited amount of charge before the potential difference changes polarity and the charge is returned to the source. The higher the frequency, the less charge will accumulate and the smaller the opposition to the current.
Both resistors and capacitors resist the flow of current when a voltage is applied. However, unlike in DC circuits, resistance may be frequency dependent. Frequencydependent resistance is known as *impedance*, a complex-valued quantity that can be broken into two parts: magnitude (the ratio of the voltage amplitude to the current amplitude) and phase (quantifies how much the current lags the voltage). Alternatively, we can break impedance down into its real and imaginary parts. Like in DC circuits, the real part of the impedance acts like resistance, resisting the flow of electric current. The imaginary part is called *reactance*, and it quantifies the opposition to a *change* in the current of a capacitive circuit element. Ideal capacitors are purely reactive, that is, they have zero resistance, and the impedance of a resistor is purely real, or resistive. Note this implies the current in a capacitor always lags the voltage by 90°. Impedance devices add like resistors in a DC circuit. For a set of components in series, the total impedance is the sum of the component impedances. To obtain the impedance of parallel circuit components, the inverse total impedance is given by the sum of the inverses of the component impedances.
Using different combinations of resistors and capacitors, RC circuits can be used to attenuate some frequencies, while allowing others to propagate through the circuit unaffected. For example, wiring a resistor in series with a load, and a capacitor in parallel with the same load, significantly attenuates high-frequency signals. Conversely, wiring a resistor in parallel with the load, and the capacitor in series, attenuates low-frequency signals. In Figure 2.4, at low frequencies, the reactance of the capacitor will be very large compared to the resistance of the resistor. This means that the voltage across the capacitor will be much larger than the voltage across the resistor. At high frequencies the 22 KYLE J. CURHAM and JOHN J. B. ALLEN
reverse is true: the voltage across the resistor is larger than across the capacitor. In other words, low frequencies pass to the output, and high frequencies are attenuated. This is known as a low-pass RC filter. Similarly, we can construct a high-pass filter by swapping the resistor and capacitor. The frequency cutoff for these *filters* is determined by the time-constant of the circuit, which is derived from the resistance and capacitance. The *cutoff frequency* for an RC circuit is:
$$f_c = \frac{1}{2\pi RC}$$
In the low-pass configuration, frequencies just above the cutoff are attenuated to half their original amplitude. Conversely, in the high-pass configuration, frequencies just below the cutoff are attenuated to half amplitude. The amount of attenuation increases as you move farther beyond the cutoff frequency. Figure 2.4 shows the amplitude roll-off as a function of frequency for a low-pass filter.

**Figure 2.4** Low-pass RC filter (left). The parallel arm with the capacitor provides a low impedance path for high frequency signals. However, the capacitor saturates for low-frequency signals, providing a high-impedance path. Low-frequencies signals are thus preferentially observed at Vout. Frequency response of the low-pass RC filter (right). The signal is not appreciably attenuated below the cutoff frequency of 50 Hz (shown in red). At frequencies just above 50 Hz, the signal magnitude is cut in half. As frequency increases, the amount of attenuation increases.
LOGIC BEHIND EEG FREQUENCY ANALYSIS 23
## **2.6 Hodgkin–Huxley Model**
We can use a simple circuit model to describe the electrical properties of neurons, including the initiation and propagation of action potentials. Action potentials are the result of the diffusion of sodium and potassium ions across neural membranes. The Hodgkin–Huxley model treats each component of a neuron as an electrical element in the circuit (Figure 2.5), where current is propagated by the movement of ions across cell membranes.
The cell membrane is represented by a capacitance (Cm). Cellular membranes are highly resistive, and act as a dielectric material due to their relatively impermeability. In the absence of special proteins called ion channels, ions like sodium and potassium are unable to diffuse across the membrane, effectively turning the membrane into the dielectric of a capacitor. As ionic currents add or subtract from the charge accumulating inside the neuron, ions line up along the cell membrane. The differing concentration of ions on either side of the membrane results in a net voltage potential, represented by voltage sources (*En*). To maintain these concentration gradients, neurons have active sodium-potassium pumps that exchange two sodium ions into the extracellular space for three potassium ions in the intracellular space.
Sodium and potassium ion channels are represented by electrical conductances (*GNA*, *GK*) that depend on both voltage and time. As the voltage potential increases, the permeability of the membrane is selectively modulated, that is, conductance is increased, for specific ion species. The flux of sodium or potassium ions across the membrane is represented by ionic currents (*Ip*). Since the membrane is not perfectly impermeable, leak channels are also included, represented by another conductance (*GL*).
The Hodgkin–Huxley circuit model exhibits similar dynamics to real neurons. The amount of injected current controls the emergence of a stable limit cycle. For a sufficiently large input current, the circuit will exhibit repeating "action potentials" at a minimum firing rate. This means that either the neuron is not firing at all (corresponding to zero frequency) or is firing at the minimum firing rate. Increasing the injected current beyond the minimum threshold increases the firing rate of the neuron. When

**Figure 2.5** Equivalent circuit diagram for the Hodgkin–Huxley model.
©2003 James M. Bower and David Beeman.
24 KYLE J. CURHAM and JOHN J. B. ALLEN
the neuron fires, a series of channel activations occur to produce the action potential. As the membrane potential approaches threshold, sodium ion channels begin to rapidly open, depolarizing the membrane (i.e., discharging the capacitor). The influx of sodium changes the voltage gradient between the intracellular and extracellular space, increasing the membrane potential. Once the polarity of the potential changes direction (when enough sodium ions have crossed the membrane), sodium ion channels begin to deactivate (decreasing sodium conductance). As the sodium channels close, potassium channels begin to open (increasing potassium conductance), resulting in an efflux of potassium ions to the extracellular space, restoring the membrane potential to the resting state following a brief hyperpolarization.
### **2.7 Filtering**
As discussed, simple RC circuits can selectively attenuate certain components or features of a signal, and not others. This is known as filtering. Filters come in a variety of forms (RC circuits, mechanical and optical filters, digital signal processing, etc.). Here we examine two of the most common digital filters used in electrophysiology. The response of a system to a brief input signal, or impulse, is called the *impulse response*. The impulse response of a *finite impulse response* (FIR) *filter* settles to zero in finite time. Given a finite sample of nonzero input values, an FIR filter will always yield a finite sample of nonzero output values. This contrasts with an infinite impulse response (IIR) filter, which does not settle in finite time. The RC filters seen in Section 2.6 are examples of IIR filters since the capacitors (or inductors) in the RC filter never completely relax following an impulse.
## **2.8 Analog-to-Digital Signal Conversion**
Most FIR filters are implemented using digital signal processing. Our discussion of electricity thus far has dealt with *analog signals*, which are continuous in both time and in voltage. An economy of representation can be achieved by sampling discrete points in both the time and voltage domains, a process of creating a *digital signal*, which has a temporal resolution determined by the *sampling rate* and a voltage resolution determined by the resolution of the *analog-to-digital converter* (Figure 2.6). For example, a 16-bit converter will allow 1016 of 65,536 discrete voltage values, and a sampling rate of 1,000 Hz will allow one value every millisecond.
With sufficiently large sampling rates, a digital signal can closely approximate the analog signal it is attempting to represent (Figure 2.7). However, several considerations
LOGIC BEHIND EEG FREQUENCY ANALYSIS 25

**Figure 2.6** A signal sampled at 20 Hz. Discrete-time sampling (left panel) allows for continuous y-axis (μV) values, whereas digitally-sampled signals (right panel) must use a limited number of y-axis values. The three bit converter illustrated here (right panel) allows for $2^{3} = 8$ distinct values, providing only a coarse approximation of the signal voltage. The right panel depicts the discrete sample value (red circle) and the 3-bit digital equivalent (red line), and the discrepancy (dashed vertical black lines).are essential to ensure signal fidelity when digitizing an analog waveform. In order to recover all components of a periodic waveform, it is necessary to use a sampling rate at least twice the highest waveform frequency. This is known as the *Nyquist sampling rate*, and it determines whether or not aliasing will occur. Similarly, for a given sampling rate,

**Figure 2.7** A comparison of a signal (black line) sampled (red line) at three sampling rates (20, 40, 100 Hz) and using three different converter resolutions (4-bit, 5-bit, and 8-bit) that allow for 16, 32, and 128 distinct μV values. Low bit-resolution was used here for illustrative purposes; commercial converters are typically 12-bit (4,096 values) or 16-bit (65,536 values).
26 KYLE J. CURHAM and JOHN J. B. ALLEN
**Figure 2.8** Signal aliasing due to insufficient sampling rate. Samples from an 18-Hz signal were sampled at a rate of 20 Hz. Identical samples are obtained for a 2-Hz sine wave sampled at 20 Hz. These digitized signals are indistinguishable from each other.
the highest frequency signal that can be represented is one-half the sampling rate, and this is known as the *Nyquist frequency*. *Aliasing* occurs when the set of samples obtained from the analog signal are indistinguishable from samples from a lower-frequency signal. For example, in Figure 2.8, an 18-Hz signal is sampled at 20 Hz, well below the Nyquist sampling rate. For this 20-Hz sampling rate, the Nyquist frequency is 10 Hz. Although the signal is in fact an 18-Hz signal, the sampled signal appears as a 2-Hz sine wave, so the signal is not well characterized. In general, signals that are *x* Hz above the Nyquist frequency will appear as a signal *x* Hz below the Nyquist frequency. Sampling above the Nyquist frequency will prevent aliasing but may still not characterize the signal well in the time domain. As a general guideline, it is recommended to sample at least 5× the highest frequency of interest to get a good signal.
### **2.9 Digital Filtering**
FIR and IIR digital filters can be used to process digital signals. A simple moving average is an example of an FIR filter. If we take the average across the last five data samples and shift the five-sample window forward by one sample at each timestep, the result is a moving average window. We can denote the value of the filtered signal (*x*) at the *n*th timepoint using summation notation:
$$y(n) = \sum_{k=-2}^{2} \frac{1}{5} x(n-k)$$
LOGIC BEHIND EEG FREQUENCY ANALYSIS 27
We can take this one step further, using a different weight for each sample in the moving average window (*h*) of width M + 1:
$$y(n) = \sum_{k=-M/2}^{M/2} h(k)x(n-k)$$
This result is exactly the impulse response when the input signal *x* is an impulse, that is, one at the middle timestep and zero at all other timesteps. Note the filter output will clearly be zero outside the range of the window, demonstrating that this is in fact an FIR filter. Figure 2.9 shows the output of a moving average filter, given a noisy input signal.
The summation operation described is known as *convolution*. In general, convolution indicates the amount of overlap of one function or kernel (*h*) as it is shifted over another function (*x*). In these examples, the convolution is simple to compute. However,

**Figure 2.9** Moving average FIR filter (top). A window size of 15 ms was convolved with noisy data to obtain the filtered signal. Low-pass IIR filter with 50 Hz cutoff (bottom).
28 KYLE J. CURHAM and JOHN J. B. ALLEN
in practice, it can be computationally expensive. In the next section, we show how to efficiently evaluate convolutions using an advanced signal-processing technique called the Fourier transform.
### **2.10 Frequency Domain**
In general, signals may have both AC and DC components. For example, you may see an AC signal that oscillates around a nonzero mean (a DC offset). Arbitrary complex signals may be approximated by the sum of two or more simpler signals. For example, we can synthesize a complex signal my summing together multiple sine waves of various frequencies. Fourier analysis is the reverse process—decomposing a signal into its constituent parts. The Fourier series approximates any complex periodic signal as a finite weighted sum of sine waves of various frequencies. The more sine waves included in the summation, the better the Fourier series can approximate the signal. In the limit that the number of frequencies included in the summation goes to infinity, the Fourier series converges to the Fourier transform. In this case, we can describe the signal as a continuous distribution, or spectrum, of frequencies, along with the phases at which each sine wave begins. The Fourier series can be applied to a wide array of mathematical, physical, and signal processing problems. Fourier analysis is now widely used across several domains, including audio, images, radar, sonar, X-ray crystallography, and more.
Rather than analyzing signals as a function of time, Fourier analysis allows us to study their properties as a function of frequency. Signals that are localized in the time domain have Fourier transforms that are spread out across the frequency domain, and vice versa. For example, the Fourier transform of a pure sine wave is a single point in the frequency domain (Figure 2.10, bottom). Points in the frequency domain may be characterized by properties such as power and phase, which are of interest for EEG analyses. The absolute value of a given frequency component of the Fourier series indicates the "amount" of that frequency present in the original signal. The squared absolute value is the signal power. The *power spectrum* describes how signal power varies as a function of frequency. EEG signals typically follow a 1/*f* trend, such that low frequencies have more power compared to high frequencies. However, the power spectrum may vary as a function of individual differences and task demands. Changes in power at a frequency may be due to alterations in the slope of the EEG frequency spectrum, or modulations in frequency-specific oscillatory activity (see Chapters 9, 10, and 23). Similarly, the *phase spectrum* of the signal can be extracted from the Fourier series. The signal phase indicates the amount of "shift" in each of the basis sine waves (for more info, see Chapter 7).
The Fourier transform is invertible. Given the power and phase spectrum, it is possible to reconstruct the original time-domain signal. Moreover, it is possible to compute the Fourier transform of a signal, perform mathematical operations in the frequency
LOGIC BEHIND EEG FREQUENCY ANALYSIS 29
**Figure 2.10** Constructing a complex signal from the superposition of sinusoids (top). The power spectrum of the signal show distinct peaks at the frequencies of the component sinusoids. A single sinusoid corresponds to a single peak in the power spectrum (bottom).
domain to alter the power and phase spectrum, and then compute the inverse Fourier transform to convert back to the time domain. For every mathematical operation in the time-domain, there is a corresponding equivalent operation in the frequencydomain. In some cases, operations may be easier to perform in one domain or another. This makes the Fourier transform very powerful. For example, convolution in the timedomain is equivalent to multiplication in the frequency domain.
30 KYLE J. CURHAM and JOHN J. B. ALLEN
To sum up: compute the Fourier transform of the time-domain signal and filter weights, multiply them in the frequency domain, and compute the inverse Fourier transform to obtain a filtered signal.
## **2.11 Windowing**
The Fourier transform assumes the signal is periodic and includes sine waves of infinite period. However, EEG recording epochs are finite, spanning just seconds or minutes. Clearly low frequencies cannot be captured by data segments smaller than the period of the signal. For example, a segment of 250 ms will contain only a half-cycle of a 2-Hz sine wave. In contrast, a 50-Hz waveform would complete 10 full cycles within the allotted window. A general rule guideline to determine an adequate window size is to take 3–5 times the period of the lowest frequency of interest.
Window functions are often used to examine small segments of data from a longer signal to study transient events that have may have different spectral properties than other surrounding data segments. Windows are usually constructed such that they are zero-valued outside of the interval, symmetric around the middle of the interval, and tapering away to zero at the edge of the window. Several types of window functions are commonly used in EEG frequency analysis, including Hann, Hamming, and Gaussian windows. The duration of the window is application specific and is governed by requirements such time and frequency resolution.
However, we cannot perfectly resolve both time and frequency simultaneously. Time and frequency are *conjugate variables*, which are coupled such that knowledge of one makes knowledge of the other uncertain. Therefore, there is a tradeoff between time and frequency resolution, such that good time resolution comes at the expense of frequency resolution, and vice versa. As the window shrinks to zero width, short tones become clicks, with no discernable frequency. Clicks can be perfectly localized in time, but the frequency is undefined. As the window gets large compared to the signal length, it becomes impossible to localize a signal in time, but the frequency can be easily determined. Time-frequency analyses balance the time-frequency resolution tradeoff.
### **2.12 Time-Frequency Analysis**
Frequency analyses are restricted to stationary signals. That is, the spectral characteristics do not change over time. However, EEG signals change as a function of state and task demands, which can vary over time. Time-frequency analyses are used to study the non-stationary characteristics of psychophysiological signals. Rather than analyzing signals in one domain—time *or* frequency—signal properties are localized to points or pixels in a two-dimensional time-frequency plane.
LOGIC BEHIND EEG FREQUENCY ANALYSIS 31
The simplest method to obtain a time-frequency representation of data is to compute the Fourier transform over a small sliding window that is chosen to be just wide enough to resolve the lowest frequency of interest. This approach yields local information about the signal, including frequency and phase content. This method is known as the short time Fourier transform (STFT) and can be used to obtain the power and phase of the signal at each point in the time-frequency plane.
The wavelet transform is slightly more advanced, considering the time-frequency trade-off that comes with windowing. This method convolves the signal with a set of complex gaussian-windowed sinusoids. When the similarity between the signal and wavelet is high, the convolution term is large. A family of wavelets of varying frequency and duration are constructed and convolved with the EEG signal to find points of peak similarity. The amplitude and phase of the signal can be obtained from the transform by computing the magnitude and angle of the complex wavelet coefficients. Unlike the STFT, the resolution of the wavelet transform has different properties at different frequencies. As frequency increases, the wavelets get shorter, effectively decreasing the window width. This leads to better time-resolution at the cost of worse frequency resolution (figure 11). In general, the wavelet transform has better time-resolution at high frequencies and better frequency resolution at lowfrequencies. For a more in-depth look at the wavelet transform, see chapters 12 and 13in Cohen (2014).
Time-frequency decompositions provide a new way to identify psychophysiologically relevant components. While traditional time-domain methods could reveal components that occur at different timepoints, they cannot distinguish between components that occur at different frequencies at the same time-point. However, once the time-frequency decomposition is obtained, new analyses may be performed that were not possible with pure time-domain or
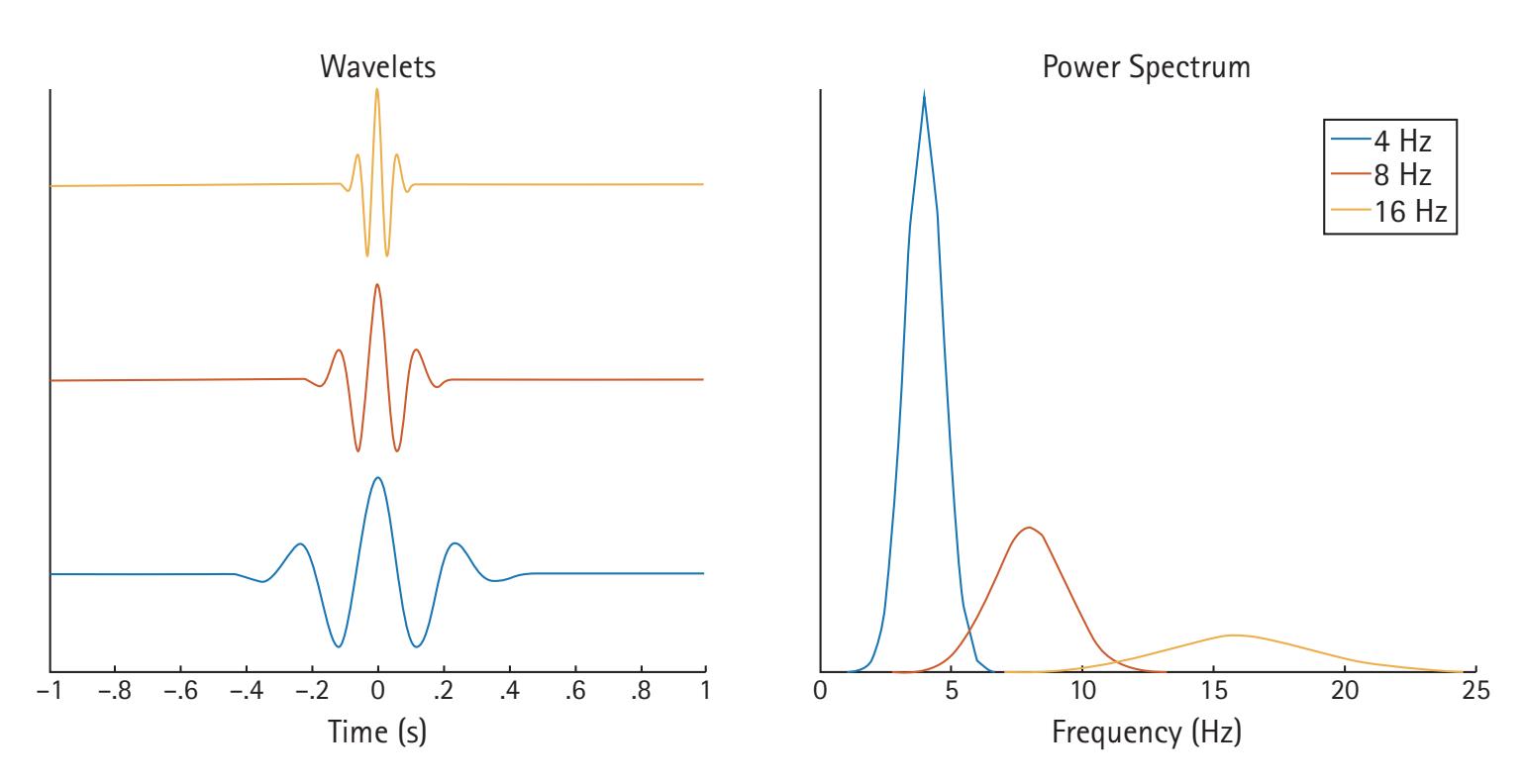
**Figure 2.11** Wavelet time-frequency resolution trade-off. Higher-frequency wavelets (yellow) are more precise in time (left), but less precise in frequency (right). Conversely, low frequency wavelets (blue) have poor time resolution (left) but good frequency resolution (right).
32 KYLE J. CURHAM and JOHN J. B. ALLEN
frequency-domain approaches. For example, the phase consistency between two or more channels over time is often used to infer frequency-specific connectivity between regions. Inter-channel phase synchrony is evaluated by computing the covariance between the phases of two or more channels at a given frequency (see Chapter 20). Time-frequency analysis allows for the identification of event-related time-locked changes that are not phase-locked; such changes would not appear in traditional time-domain analyses using signal averaging to create event-related potentials (cf. Trujillo & Allen, 2007).
### **2.13 Practical Considerations for EEG**
#### **2.13.1 EEG Signal Artifacts**
EEG is used to record electrical activity originating in the cerebral cortex, although it also detects electrical activity arising from sources other than the brain. EEG signals are highly sensitive and are easily influenced by electrical activity in the surrounding environment. Artifacts in EEG signals come in at least two distinct varieties: physiological and non-physiological noise. EEG signals generated by the body, but that are not cerebral in origin, are deemed physiological noise. Sources of physiological artifact include muscle movements, eye blinks, tongue movements, respiration sway, electrocardiographic activity, jaw clenching, etc. Conversely, non-physiological artifacts arise from sources outside the body, such as electronic noise, amplifier saturation, or loose electrodes. For example, thermal noise due to the random motion of electrons in resistive components, flicker due to irregularities in contact pins, and burst due to semiconductor impurities are common sources of noise. The most obvious electronic noise is flicker due to power-line interference, appearing at 60 Hz in North America and 50 Hz in much of the rest of the world. When the electrical impedance at the scalpelectrode interface is high (>5 k*Ω*), resulting in a poor connection, the electrode is more sensitive to these noise sources. To judge the acceptability of the scalp impedance for obtaining good quality signals, it is important to consider the input impedance of the amplifier. Contemporary high impedance amplifiers mitigate the susceptibility to electronic noise, as the fidelity of the observed EEG signal is directly related to the average impedance of the target and the reference electrode, and inversely related to the amplifier input impedance (Ferree et al., 2001). Thus some equipment can produce high quality signals with scalp impedances that may be higher than the often-used 5 k*Ω* standard.
There are multiple strategies to handle EEG recording artifacts: use of a ground electrode to remove noise that presents similarly across all electrodes, artifact rejection to remove electrodes or segments of data that are corrupted by noise, and artifact correction to separate signal from noise without sacrificing data.
LOGIC BEHIND EEG FREQUENCY ANALYSIS 33
#### **2.13.2 Grounding**
Ground electrodes are used for common mode rejection: parts of the signal shared across all electrodes are removed from the recording. A good ground connection is critical to reducing the impact of external noise sources. Impedances for all electrodes are compared to the ground electrode. Therefore, if the ground impedance is high, good impedances will not be possible on any other electrodes. However, electrical interference may persist even after ensuring good electrode impedances and secure grounding. Therefore, data rejection and correction are often used to handle residual artifacts during offline processing.
#### **2.13.3 Artifact Rejection**
Artifact removal may consist of rejecting entire segments of data, or individual electrodes from the recording. While the basic strategy is to identify data corrupted by artifact and exclude it from future analysis, it is not a trivial task. The determination of whether a signal is sufficiently corrupted by noise to justify removal is time consuming, subjective, and may vary by researcher. Moreover, significant training is required to learn to correctly identify different sources of noise. Judgements must also be made as to whether each artifact should be removed, even if it is correctly identified. In some cases, a filter may be used to attenuate electronic noise. For example, a 60-Hz artifact from power-lines may be removed from EEG recordings using a notch filter, which allows frequencies lower and higher than the specified frequency-band to pass unaffected, while significantly attenuating the artifact (e.g., between 55–65 Hz). However, filtering may not be an optimal solution for all artifacts. For example, blink timing is related to information processing (Stern et al., 1984), and blink rate is correlated to dopamine release (Taylor et al., 1999), although recent work has called this into question (Dang et al., 2017). However, many researchers remove data segments with eyeblinks due to the large artifact they produce in frontal EEG channels. If the phenomenon of interest is correlated to these physiological artifacts, it is possible to inadvertently remove valuable data and miss the psychophysiological phenomenon.
Sometimes artifacts may be localized to a single bad channel. In this case, remove only that channel from the recording and keep the remaining data. Many researchers examine the standard deviation of the signal to automatically detect bad electrodes. If it exceeds a threshold much larger than would be expected for a quality EEG signal, the channel is marked bad. If a channel is marked bad and it is required for a planned EEG analysis, the missing data can be interpolated. Interpolation uses information from the surrounding electrodes to guess what the signal would have been if there were a good electrode at that location. A popular choice is spherical spline interpolation (Perrin et al., 1989).
34 KYLE J. CURHAM and JOHN J. B. ALLEN
#### **2.13.4 Artifact Correction**
If possible, EEG researchers want to retain as much signal as possible and thus avoid removing noisy signals from data analyses. Several algorithms exist to attempt to separate signal from noise, thereby sparing valuable data. The three most common approaches are linear regression, independent component analysis (ICA), and principal component analysis (PCA).
Linear regression is by far the simplest method to remove ocular artifacts. Ocular artifacts typically have much higher amplitude than the EEG signals generated by neural sources. For the purpose of regression, the tiny EEG signals are assumed to be noise relative to the ocular artifacts. Blinks are assumed to affect electrodes in a linear combination, such that electrodes closer to ocular channels have a larger weight than electrodes farther from ocular channels. Once the optimal weights are calculated, a weighted composite of the ocular artifact is subtracted from each of the EEG electrodes (cf. Gratton et al., 1983), yielding EEG that should be (mostly) free of the artifact. However, it requires the ocular artifacts to be linearly dependent and normally distributed, which generally is not the case. This approach is fast and simple, but sometimes inaccurate, which introduces another source of residual artifact. Errors in the regression get "subtracted into" the recording.
ICA is a blind source separation technique, unmixing a multivariate signal into a set of additive components (Delorme et al., 2010). Unlike linear regression, independent components (ICs) are assumed to be non-Gaussian and statistically independent from each other. However, ICA can only separate linearly mixed sources, and even when the sources are not independent, ICA will return maximally independent components. In many cases, a subset of the ICs will capture artifacts such as ocular and motor components. Components are determined to be artifact or signal based on their similarity with the topography and time course of known artifacts. This can be determined based on experimenter ratings or algorithmically using spatial and temporal features of eye blinks, vertical and horizontal eye movements, and discontinuities in the EEG time series (Mognon et al., 2011). Artifactual components may also be identified automatically based on a supervised machine learning approach trained from expert ratings on a large corpus of EEG data (Winkler et al., 2014). ICA is more useful than linear regression because it can extract more than just ocular components, also capturing loose electrodes and muscle artifacts equally well. Once the bad components are identified, the signal can be reconstructed without the artifacts.
Other blind source separation techniques similar to ICA can be used in a similar manner. PCA is like ICA in that it separates the data into a set of linearly independent components. However, these components are additionally assumed to be mutually orthogonal (i.e., uncorrelated with each other).
#### **2.13.5 Referencing**
Voltage is always measured between two points. It does not make sense to talk about the potential at a particular EEG electrode without first defining a reference potential (i.e., LOGIC BEHIND EEG FREQUENCY ANALYSIS 35
an arbitrarily chosen "zero"). A common reference is usually chosen for all electrodes, to which all potentials recorded at each electrode are measured. The reference needs to be chosen carefully because the electrical activity under the reference site will be reflected in the activity at every other electrode. If the reference is not neutral, artifacts will be introduced due to the activity at the reference site. The reference electrodes should be placed on a presumed electrically neutral area. In many cases, researchers choose an electrode over the mastoid part of the temporal bone, or the left or right earlobe.
In reality, there are no electrically neutral points to choose as a reference. However, it is possible to construct a virtual reference that is more likely to be electrically neutral than any single EEG electrode. For example, choosing the left or right mastoid alone results in a systematic decrease of EEG amplitude in the electrodes which are closer to the reference site. The "linked" mastoids reference is obtained by using the average of both left and right mastoid electrodes as the reference level. This resolves the left/right asymmetry that would normally occur. Another popular choice is the average reference when the number of electrodes is large (typically >32). The average reference is obtained by subtracting the mean potential across all EEG electrodes from each electrode at each time-point. Theoretically, if we could obtain measurements sampling equally around a sphere containing the brain, then electric dipoles picked up by the electrodes would average out to zero, and the average reference would be a truly neutral point (Bertrand et al., 1985). However, this is a practical impossibility because the ventral surface is inaccessible for electrode placement. Still, by averaging the electrical activity across the entire scalp, the "responsibility" is distributed over all electrodes, rather than only one or two of them.
However, prominent deflections at any given scalp location can differ dramatically depending on the chosen reference scheme, affecting both the amplitude and latency of the recorded signal. Not all researchers use the same reference, leading to problems in the comparability between datasets. Fortunately, it is possible to convert from one reference to another with a simple mathematical transformation. Note the potential difference between two electrodes does not depend on the chosen reference. If your analysis is only concerned with comparisons between two electrodes, then the reference is irrelevant. A simple analogy is measuring height above sea level. A change in sea level does not change the shape of the landscape or the relative elevation between any two points. Thus, if there is a change in sea level, we can readjust to the new reference level by simply subtracting the change in elevation from every point. Similarly, we can transform between different references by subtracting the potential at the chosen reference site.
Other transformations can be used to obtain a reference-free representation of EEG signals. This is usually achieved using the scalp Laplacian, sometimes called the Current Source Density (CSD). Technically, the scalp Laplacian relates current generators within an electrical conductor to the second spatial derivative of the potential at each electrode. Approximately, the scalp-Laplacian at a given electrode is obtained subtracting the potentials of all neighboring sites weighted by their inverse distance. In other words, the scalp Laplacian measures how extreme the potential at one electrode is compared to the average of its neighboring electrodes. This intuitive description is complicated by the fact that scalp electrode montages do not form a flat grid of evenly spaced electrodes.
36 KYLE J. CURHAM and JOHN J. B. ALLEN

**Figure 2.12** Topography of alpha power under eyes open (top) and eyes closed (bottom) conditions as a function of transformation (Cz, average (AR), or linked mastoid (LM) reference or current source density (CSD) transformation) from a sample of over 2400 resting recordings. Power values at each site represent natural-log transformed values; thus, negative numbers represent mean power values less than one. Each transformation is scaled independently, but within each transformation, eyes open and closed data are plotted on the same scale. Only the CSD transformation confines occipital alpha to occipital leads, whereas the other three montages show reflected alpha at frontal regions, visible most clearly by a comparison of frontal leads under eyes closed compared to eyes open recordings.
Figure modeled after Smith et al., 2017.
Instead, they conform to the nearly spherical geometry of the scalp. However, the Laplacian can still be efficiently computed using spherical spline interpolation (Delorme & Makeig, 2004). The scalp Laplacian has the added advantage of addressing volume conduction. Electrical fields originating from any particular neuronal structure will influence the electrical potential throughout the brain and surrounding physiological tissue. As a result, EEG electrodes detect a mixture of activity from across the whole brain, rather than directly under the recording site. Critically, the scalp Laplacian minimizes the influence of this effect since the Laplacian is close to zero when a signal is shared similarly across several electrodes (cf. Smith et al., 2017). Figure 2.12 shows a comparison across referencing schemes .
### **2.14 Conclusion**
A basic understanding of electricity and signal processing is vital to EEG data collection and interpretation. Investigators need to report clearly how they acquired and analyzed the data, and consumers need to be able to evaluate the methods and claims critically. There are many steps to be taken in acquiring and processing EEG signals, from net application and impedance checking, to grounding and referencing, to artifact detection LOGIC BEHIND EEG FREQUENCY ANALYSIS 37
and correction, to data processing and analysis methods in the time and frequency domains. This chapter provided a basic introduction to these concepts, but more information can be obtained from several guidelines papers (Picton et al., 2000; Keil et al., 2014).
### **Glossary**
**Aliasing:** When an analog signal is insufficiently sampled, the digitized signal may be indistinguishable from samples from a lower-frequency signal.
**Ampere:** The SI unit of electric current. It is defined as one coulomb of charge per second.
**Analog signal:** A continuous time-varying signal that may vary in frequency, amplitude, and phase.
**Analog-to-digital converter:** System that converts an analog signal into a digital signal.
**Capacitance:** Ratio of the change in an electric charge to the change in electric potential. A property that quantified a materials ability to store electric charge.
**Conductivity:** Property that quantifies how strongly a material conducts electric current.
**Conductor:** A material that allows the flow of electric current.
**Conjugate variables:** Pairs of variables that cannot be precisely estimated simultaneously. Knowledge of one variable necessitates uncertainty in the other variable. Time and frequency are examples of conjugate variables.
**Convolution:** A mathematical operation that indicates the amount of overlap of one function or kernel as it is shifted over another function.
**Cutoff frequency:** Frequency at which the signal power is reduced by half. The amount of attenuation increases as you move farther from the cutoff.
**Current:** The directed motion of electrons or electric charge.
**Digital signal:** A discrete sequence of finite values that represent a signal.
**Electric field:** The force per unit charge at each point in space.
**Electricity:** Phenomenon that describes the behavior and movement of electric charge.
**Electromotive force (EMF):** The rate at which energy is drawn from a 1 A current source, measured in volts.
**Finite impulse response (FIR) filter:** A filter whose impulse response settles to zero in finite time.
**Free electrons:** Any electron that is free to move under the influence of an electric or magnetic field.
**Impedance:** Measures the opposition to an electric current when a voltage is applied. Impedance is equal to resistance in a DC circuit.
**Impulse response:** The output of a circuit when presented with a brief input signal.
**Insulator:** A material that does not allow the flow of electric current.
**Ionization:** The acquisition or loss of electrons in an atom or a molecule, resulting in a net positive or negative charge.
**Nyquist frequency:** Half of the sampling rate of a digital signal. It is the highest frequency that can be accurately sampled for a given sampling rate.
**Nyquist sampling rate:** In order to adequately digitize an analog signal, it should be sampled at least twice the highest frequency of interest.
38 KYLE J. CURHAM and JOHN J. B. ALLEN
**Phase spectrum:** A measure of signal phase versus frequency.
**Potential energy:** The energy stored by an object due to electric charge.
**Power spectrum:** A measure of signal power versus frequency.
**RC time constant:** The time required to charge a capacitor to 63.2% of the applied DC voltage. **Reactance:** Material property that measures the resistance to a change in current or voltage.
**Resistance:** Property that quantifies how strongly a material resists electric current.
**Sampling rate:** Rate at which discrete samples are acquired for a digital signal.
**Volt:** The amount of EMF required to push a current of one ampere through a conductor with a resistance of one ohm, or 1 volt/ampere.
**Voltage:** Difference in electric potential between two points.
### **References**
Bertrand, O., Perrin, F., & Pernier, J. (1985). A theoretical justification of the average reference in topographic evoked potential studies. *Electroencephalography and Clinical Neurophysiology*, *62*(6), 462–464.
Cohen, M. X. (2014). *Analyzing neural time series data: theory and practice.* MIT press.
Dang, L. C., Samanez-Larkin, G. R., Castrellon, J. J., Newhouse, P. A., Zald, D. H., Perkins, S. F., & Ronald, L. (2017). Spontaneous eye blink rate (EBR) is uncorrelated with dopamine D2 receptor availability and unmodulated by dopamine agonism in healthy adults. *ENeuro*, *4*(5), 1–11.
Delorme, A. & Makeig, S. (2004). EEGLAB: An open source toolbox for analysis of singletrial EEG dynamics including independent component analysis. *Journal of Neuroscience Methods*, *134*(1), 9–21.
Delorme, A., Sejnowski, T. J., & Makeig, S. (2010). Enhanced detection of artifacts in EEG data using higher-order statistics and independent component analysis. *NeuroImage*, *34*(4), 1443–1449.
Ferree, T. C., Luu, P., Russell, G. S., & Tucker, D. M. (2001). Scalp electrode impedance, infection risk, and EEG data quality. *Clinical Neurophysiology*, *112*(3), 536–544.
Gratton, G., Coles, M. G., & Donchin, E. (1983). A new method for off-line removal of ocular artifact. *Electroencephalography and Clinical Neurophysiology*, *55*(4), 468–484.
Keil, A., Debener, S., Gratton, G., Junghöfer, M., Kappenman, E. S., Luck, S. J., Luu, P., Miller, G. A., & Yee, C. M. (2014). Committee report: Publication guidelines and recommendations for studies using electroencephalography and magnetoencephalography. *Psychophysiology*, *51*(1), 1–21.
Mognon, A., Jovicich, J., Bruzzone, L., & Buiatti, M. (2011). ADJUST: An automatic EEG artifact detector based on the joint use of spatial and temporal features. *Psychophysiology*, *48*(2), 229–240.
Perrin, F., Pernier, J., Bertrand, O., & Echallier, J. F. (1989). Spherical splines for scalp potential and current density mapping. *Electroencephalography and Clinical Neurophysiology*, *72*(2), 184–187. [https://doi.org/10.1016/0013-4694\(89\)90180-6](https://doi.org/10.1016/0013-4694(89)90180-6)
Picton, T. W., Bentin, S., Berg, P., Donchin, E., Hillyard, S. A., Johnson, R., . . . Taylor, M. J. (2000). Guidelines for using human event-related potentials to study cognition: recording standards and publication criteria. *Psychophysiology*, *37*(2), 127–152. [http://www.ncbi.nlm.](http://www.ncbi.nlm.nih.gov/pubmed/10731765) [nih.gov/pubmed/10731765](http://www.ncbi.nlm.nih.gov/pubmed/10731765)
LOGIC BEHIND EEG FREQUENCY ANALYSIS 39
- Smith, E. E., Reznik, S. J., Stewart, J. L., & Allen, J. J. (2017). Assessing and conceptualizing frontal EEG asymmetry: An updated primer on recording, processing, analyzing, and interpreting frontal alpha asymmetry. *International Journal of Psychophysiology*, *111*, 98–114.
- Stern, J. A., Boyer, D., & Schroeder, D. (1994). Blink rate: A possible measure of fatigue. *Human Factors*, *36*(2), 285–297.
- Stern, J. A., Walrath, L. C., & Goldstein, R. (1984). The endogenous eyeblink. *Psychophysiology*, *21*(1), 22–33.
- Trujillo, L. T., and Allen, J. B. (2007). Theta EEG dynamics of the error-related negativity. *Clinical Neurophysiology*, 118(3), 645–668
- Taylor, J. R., Elsworth, J. D., Lawrence, M. S., Sladek, J. R. Jr, Roth, R. H., & Redmond, D. E. Jr. (1999). Spontaneous blink rates correlate with dopamine levels in the caudate nucleus of MPTP-treated monkeys. *Experimental Neurology*, *158*(1), 214–220.
- Winkler, I., Brandl, S., Horn, F., Waldburger, E., Allefeld, C., & Tangermann, M. (2014). Robust artifactual independent component classification for BCI practitioners. *Journal of Neural Engineering* [online], *11*(3), 035013.
# [CHAPTER 3](#page-5-5)
# [FROM NEURAL OSCILL ATIONS](#page-5-5) [TO COGNITIVE PROCESSES](#page-5-5)
ANDREAS KEIL AND NINA THIGPEN
## **3.1 Oscillations in Complex Systems: An Overview**
Cyclical rhythms are a hallmark property of natural systems, from the movement of the planets to the sleep and wake cycles of mammals, to neuronal membranes. Such rhythmic variation, if it occurs repeatedly across time, is called an *oscillation*. The backand forth of tree branches on a windy day, ocean waves, and the rhythmic song of choir frogs are further examples for natural oscillations. As such, the notion of oscillations seems fairly straightforward: they occur in complex systems, in which many connected units interact, and they reflect activity perceived as recurrent, or rhythmic. However, a woman strolling on an ocean beach will soon realize that although waves break repeatedly and somewhat predictably, they also vary in terms of their exact timing, duration, size, and shape. This seems to be different from the orbit of our planet earth around the sun, or the vibrations of crystalline matter—rhythms that are regular and fixed enough for us to measure time on their basis. These latter are typically referred to as "periodic oscillations", which are a sequence of recurring events (often taking the shape of a wave when measured), each of which has identical, constant, duration. Although periodic oscillations are well defined in the language of mathematics (e.g., the sine function), the examples at the start of the chapter show that the concept of periodicity may not be as clear-cut in natural systems. For example, the duration of solar years is not constant when measured with precision, and even clock-setting crystal oscillators change their rhythm with temperature. Thus, periodicity may be a continuous dimension ranging from more periodic (the solar year) to less periodic (the tides) rhythms, rather than representing a qualitative (yes/no) feature. In fact, various natural systems are likely to FROM NEURAL OSCILLATIONS TO COGNITIVE PROCESSES 41
oscillate in different fashion, and the same system may display oscillatory behavior at different levels of complexity when challenged in different ways.
Identifying how a complex system oscillates may go a long way towards its characterization. As a consequence, the natural sciences have developed an impressive toolbox for detecting, quantifying, and understanding oscillatory activity, and to separate it from non-oscillatory phenomena. This chapter discusses how these concepts are applied to fundamental problems in cognitive neuroscience, and ask what the significance is of oscillatory activity for human behavior and cognition? It also asks how we should define and conceptualize brain oscillations, and how they can be measured and interpreted. We address these questions in the light of current research, with a focus on electrophysiological recordings in human beings and experimental animals.
## **3.2 Brain Oscillations and Behavior—an Example**
After over a decade of testing, in 1927 Hans Berger conducted the earliest in vivo recordings of electric fields from the human brain using his new invention, the electroencephalograph (Berger, 1929). Upon visual inspection of these first brain wave (electroencephalography, or EEG) recordings, Berger decided that the most salient feature of the EEG was its change in frequency content when the participant performed a task or was stimulated (often by being touched with a glass probe). Most prominently, Berger identified "first-order waves" oscillating at a rate of 10 cycles/second (i.e., 10 Hertz (Hz), today referred to as *alpha waves*) and faster "second-order waves" oscillating at about 20–30 Hz (today referred to as *beta waves*). Even without the ability to average across trials, and in the absence of digitally supported spectral analysis, Berger and his colleagues (i.e., his family; his wife Ursula von Bülow was his technical assistant and frequent test participant, along with himself, and his son, Klaus) made a striking observation: whenever a person was at rest, for example, with their eyes closed, first-order waves characterized by large-amplitude regular activity at 10 Hz dominated the EEG. However, touching the person with a glass probe, asking them to open their eyes, or just addressing them and asking a question led to a dramatic blocking of these alpha waves, which were replaced by faster and lower-amplitude EEG readings. This effect, referred to as "alpha blocking" has since been replicated thousands of times, and is still used today in clinical usage of EEG in neurology and psychiatry to assess the status of global brain electric states (Başar & Güntekin, 2012). Furthermore, this observation opened an avenue for experimental studies of EEG-behavior relations, in which participants are asked to respond to experimenter-defined task demands, and changes in the EEG are measured as a dependent variable (Klimesch et al., 2005). In addition to testing hypotheses about brain function, these variables possess practical value for 42 ANDREAS KEIL and NINA THIGPEN
testing hypotheses about behavioral and cognitive processes, their time course, and about specific characteristics of the participant or the environment, of interest in clinical and translational studies.
## **3.3 Quantifying and Categorizing Brain Oscillations**
Oscillatory activity is typically described by quantifying its frequency, amplitude (power), and phase (Figure 3.1). Frequency refers to the rate of repetition of the oscillatory event (e.g., action potentials emitted by a neuron, or epileptic spikes in the EEG signal) and is measured in Hz, the number of events per second. Amplitude reflects the magnitude of the oscillatory signal at a given frequency, analogous to measuring the height of ocean waves. Power (e.g., microvolts squared) is often used instead of amplitude to describe the magnitude of an oscillation. This reflects the fact that the computation of spectral magnitude usually involves an integral across time, which may be thought of as an area under the curve at a given frequency, resulting in a squared unit of measurement. Thus, in many cases, depending on scaling and other normalization steps, power values given in published research may be roughly equivalent to the squared amplitude of the oscillatory signal.
The phase of an oscillation is a measure of its position in time, relative to a pre-defined cycle, or relative to a reference oscillation at the same frequency. Because oscillations are by definition cyclic and recurrent, phase is measured using circular metrics, typically in degrees or radians of arc. For example, a phase of 90 degrees (1/2 Pi) may indicate that the oscillation at this point in time is at its peak, going down, 180 degrees (Pi) may indicate that it is transitioning through zero, and 270 degrees may indicate that it is at its minimum, going up. In neuroscience studies, phase is often used to quantify the amount of temporal correspondence or similarity between two signals, measured

**Figure 3.1** Illustration of oscillatory power, phase, and frequency. Oscillations are characterized these three properties and can independently vary along these three dimensions.
FROM NEURAL OSCILLATIONS TO COGNITIVE PROCESSES 43
during different trials or at different locations (i.e., phase-locking, phase synchrony) [cross ref Chapter 20 Makeig and Palva]. We discuss phase-locking later in this chapter.
There are different ways for computing the oscillatory content of a signal, many of which are discussed in this volume [cross ref Chapter 23 Allen and Voytek]. Broadly, there are two main groups of methods for estimating spectral events in neural time series data. First, methods that result in a spectral representation, or frequency-domain representation. In these representations, frequency (in Hz) is plotted along the x-axis, and spectral power (or phase) along the y-axis. Power (and phase) values for each frequency in the spectrum are obtained by integrating the information across all time points entering the spectral analysis, which often is a variant of the well-known Fourier transform that uses sine and cosine functions as templates for quantifying the oscillatory content of a time-varying neural signal such as EEG or local field potentials. A second approach is used when researchers wish to retain information on the changes in oscillatory activity in their signal over time. Many methods exist for obtaining such a time-frequency representation, in which time is typically plotted on the x-axis, frequency along the y-axis, and a colormap or 3rd dimension in the figure is used to represent spectral power or amplitude for each time point and frequency. Often, this type of data analysis is used when the data set contains a substantial number of trials, locked to events (e.g., the onsets of a stimulus, the time of a motor action). Then, the timefrequency representations of each trial are compared and/or averaged. Figure 3.2 shows an example of the change in oscillatory power during a complex sequence of visual cues and behaviors as participants perform a working memory task. Wavelet analysis is a popular approach for obtaining time-frequency representations in studies of oscillatory brain activity, but many other methods exist (see Chapter 4). For a practical introduction, we recommend Cohen's *Analyzing Neural Time Series Data* (2014).

**Figure 3.2** Oscillatory changes during a working memory task. Time-frequency decomposition of the EEG activity recorded at sensor Pz over a 9-s trial in which participants memorized the orientation of two gratings. They then viewed a mask, a task array, and finally were asked to indicate if the orientation of an item in the task array matched an item in the memory set. Each task element prompts specific time-frequency dynamics. For example, alpha-band activity (8– 12Hz) is highest during the fixation period before the start of the trial, and during the retention interval when viewing the mask.
44 ANDREAS KEIL and NINA THIGPEN
A useful approach for a classification of the brain's oscillatory activity is the widelyadopted nomenclature first introduced by Robert Galambos (1992). Considering brain oscillation across several species, Galambos distinguished:
- 1. spontaneous oscillations, which are not related to external stimuli;
- 2. evoked oscillations, which are elicited and precisely time-locked to the onset of an external stimulus;
- 3. emitted oscillations, which are time-locked to a stimulus that was expected but then did not occur; and
- 4. induced oscillations, which are prompted by a stimulus but are not time- and phase-locked to its onset.
Investigators new to the field are often curious about how different types of oscillations should be analyzed and interpreted in terms of hypotheses regarding a specific behavioral, cognitive, or neural process. To address these questions, it may be helpful to consider the different types of dependent variables that may be used in studies of oscillatory brain activity during cognitive processing.
## **3.4 Characterizing Brain Oscillations in the Context of Cognitive Tasks**
The mathematical foundations of extracting power and phase from time domain neural signals as described earlier are straightforward and yield estimates of power at a given frequency, in a given time period, at a specific sensor. What is less clear is the functional and neurophysiological interpretation of differences in power, especially in populationlevel signals, such as local field potentials (LFPs), intra- and extracranial EEG, and MEG. These signals reflect the synchronous synaptic (dominantly post-synaptic) currents of a large number (at least several tens of thousands in the case of EEG/MEG) of neurons which need to be aligned favorably (in parallel) to create measurable extracranial electric fields (Olejniczak, 2006). Thus, a difference between two experimental conditions, say in EEG alpha-band power, may reflect differences in the number of neurons engaged in the respective cognitive process, but it may also represent a combination of differences in active population size, amount of dendritic engagement at each neuron, orientation of neurons involved, and temporal synchronization of the post-synaptic events. Neural mass power in a given frequency band is therefore difficult to map directly onto a physiological or cognitive concept, emphasizing the need for research that links measures of oscillatory brain activity to robust cognitive or behavioral processes, across different levels of observation (i.e., from single neurons to large populations).
In addition to measuring spectral power, researchers may use approaches that capitalize on additional spectral information, often the phase of the signal. Many algorithms FROM NEURAL OSCILLATIONS TO COGNITIVE PROCESSES 45
exist for quantifying the similarity of the phase across different observations, such as experimental trials, time points, or channels. The resulting metrics are referred to as indices of phase-locking or phase coherency. These variables are often used to estimate the strength of oscillatory interactions across recordings sites (e.g., inter-site phase locking, often considered a proxy of connectivity), the stability of the temporal profile of oscillations across repeated trials (e.g., phase-locking value), or the interactions between different frequencies within or across recordings sites (e.g., phase-amplitude coupling (Chapter 20). Thus, a wide range of hypotheses and, increasingly, formal computational models of neurophysiological processes can be tested using these different variables, each of which may reflect entirely different facets of oscillatory brain activity. Later in this chapter we present examples for using these markers across a wide range of research questions in cognitive neuroscience.
## **3.5 What's in a Band? the Traditional Demarcation Of Oscillatory Events By Frequency**
In the many decades since Berger's and many others' discoveries, brain oscillations have been traditionally divided into frequency bands in the 1–4 Hz range (delta), 4–8 Hz (theta), 8–12 Hz (alpha), 12–30 Hz (beta), and >30 Hz (gamma), with some variability in the demarcation of these bands. These frequency bands have been consistently observed at the level of spike trains, local field potentials, and EEG/MEG, making them apparent in multivariate analyses and meta-analyses across studies and even species (Lopes da Silva, 1991). The peak frequency in each of these bands is similar across bats, mice, rats, cats, dogs, horses, dolphins, macaques, and humans, despite the range of brain size and axon length across these species (Buzsáki et al., 2013). Given this phylogenetic stability, it has been suggested that the traditional frequency bands (and perhaps their logarithmic distance from one another) represent fundamental mechanisms underlying specific neurocomputations and behaviors (Steriade et al., 1990). Klimesch (1999) highlights the variability and task-dependency of these frequencies, however, with examples for gamma-like oscillations in the traditional beta band, and overlap between alpha and beta band oscillations, along with pronounced inter-individual differences. Similarly, limitations of assigning specific functional roles to oscillations in one of the traditional bands have been made apparent by phenomena in which oscillations continuously transition from one traditional band into another during the same task (Donner & Siegel, 2011).
Some of the stated confusion about these observations may be reflective of researchers' desire to equate oscillatory activity in one frequency range with a category of cognition of behavior, defined in the language of cognitive psychology, such 46 ANDREAS KEIL and NINA THIGPEN
as "alpha-blocking reflects attention", "gamma reflects feature binding", and similar notions. Such interpretations, which may be seen as examples for the problematic approach of reverse inference (Poldrack, 2011), have been considered less fruitful than, and have increasingly been replaced by, research aiming to characterize specific oscillatory correlates of a specific, quantifiable, behavior. With the advent of neurostimulation and neuromodulation techniques such as transcranial magnetic stimulation (TMS), direct current stimulation, neurofeedback, etc., recent research has also attempted to establish the causal role of oscillatory brain activity for specific cognitive and behavioral processes (Herrmann et al., 2016; Chapter 22 this volume). To understand how oscillatory activity relates to cognition, it is helpful to consider the rich neurophysiological literature based on work in experimental animals. This body of work has begun to outline neuromechanistic accounts for the emergence of brain oscillations and their relation to behavior. Importantly, these studies help to overcome the focus on one spatial scale (e.g. oscillations at membranes, in action potential, in circuits, or areas), and instead describe the rhythmic interplay between these levels of observation.
## **3.6 Oscillations at Different Levels of Observation: From Single Neurons to Neural Populations**
Since the inception of brain electrophysiology, researchers measuring electrical potentials from individual neurons, or from groups of neurons, have noted the oscillatory character apparent in neural time series (Bernstein, 1868; Marrazzi & Lorente de No, 1944). Spatial scales of these observations are typically categorized into the microscale, mesoscale, and macroscale, where microscale refers to processes at single neurons, mesoscale to small functional units such as cortical columns, and macroscale to population responses of several tens of thousands of neurons (Nunez & Srinivasan, 2006). Recent work increasingly focused on interactions between oscillations across these levels of observation, for example, by linking the rate of action potentials (spikes) to oscillatory events at different spatial scales, and at different temporal rates (Lisman & Jensen, 2013; Schroeder & Lakatos, 2009). Although a comprehensive review of this literature is outside the scope of this chapter, a number of neurophysiological and computational principles of oscillatory processes within and across different scales are now widely accepted. These principles are discussed next.
At the core of many theories of brain oscillations is the observation that time series of action potentials (i.e., spike trains) tend to contain bursts of spikes. A burst represents a rapid sequence of action potentials, a group in time, which may vary in temporal rate, providing one potential source of oscillatory pace making. The frequency at which bursts occur (i.e., the inter-burst interval) has also been shown to relate to FROM NEURAL OSCILLATIONS TO COGNITIVE PROCESSES 47
neurophysiological and behavioral processes, thus providing a second way for action potentials to temporally organize downstream neural—and ultimately behavioral processes (Gütig, 2014). Such a temporal organization may be propagated in space if neurons act as coupled oscillators, facilitating specific phase relationships among the units of a functional network of connected neurons. Many such "coupled oscillator" models of neural oscillations exist, aiming to explain how temporal signatures are shared among populations of neurons (Moon et al., 2015; Naze et al., 2015). Recent empirical work as well as work in computational modeling has converged to suggest that such coupling involves not only action potentials but a range of mechanisms that also involve subthreshold and synaptic events, along with potential changes at glia cells (Buzsáki et al., 2012).
It is now well established that spike timing, that is, the timing of action potentials, is related to synaptic oscillations measured by local field potentials, likely both driving and being driven by these synaptic fields. This research has also demonstrated that subthreshold oscillations at membranes and post-synaptic potentials constrain the spiking rate of individual neurons and may also play a role in coordinating the firing among different neurons (Mazzoni et al., 2010). This is important because it demonstrates the interplay of all-or-nothing neuronal communication and postsynaptic events, opening avenues for research that identifies the convergent versus complementary roles of oscillations at different levels, within and across neurons, in behavioral and cognitive processes.
Research in human participants has increasingly made use of intracranial data obtained from patients under pre-surgical evaluation for neurological disorders, with implanted sensor arrays (Parvizi & Kastner, 2018). In these studies, one striking discrepancy arises between levels of observation regarding the frequency content of intracranial recordings vis-à-vis extracranial recordings. Intracranial recordings, for example, electrocorticogram (ECoG) data, tend to contain robust high-frequency oscillations (Osipova et al., 2008), which are small and less reliably observed in extracranial recordings such as EEG or MEG (Yuval-Greenberg et al., 2008). This salient difference between intracranial and scalp recordings may reflect the orders of magnitude difference in the summation of electrical potentials that comprise each signal. For example, the local field potential recorded from an intra-cranially sensor embedded in cortical tissue is thought to measure the extracellular electrical fluctuations of a few hundreds to thousands of neurons, while EEG data is thought to require synchrony across a few millimeters of cortex before any fluctuations are observed on the scalp (Nunez & Srinivasan, 2006). Based on simulations and in vitro studies, some authors suggest that postsynaptic changes at dendritic trees of 40,000 to 100,000 pyramidal cells are required to cause EEG changes in the 1–2 microvolt range—if the dendrites of these neurons are oriented in parallel, generating an open electric field, required for extracranial measurement. By contrast, ECoG and LFP data are thought to reflect activity in differentially oriented cells, including contributions from interneurons, pyramidal cells, and glial cells (Buzsáki et al., 2012). Thus, EEG oscillations reflect activity in a more specific subset of neurons than ECoG and LFP but integrated over a wider distribution of space.
48 ANDREAS KEIL and NINA THIGPEN
Inter-scale oscillatory interactions also depend on the strength of the sensory input. Studies in macaque monkeys have shown that increasing the luminance contrast of a visual stimulus similarly affected spike trains, local field potential in intracranial electrodes over V1, and MEG signals, up to a contrast level of 60%. However, at levels above 60% luminance contrast, nonlinearities were observed: The MEG gamma continued to increase but the LFP gamma saturated, and in fact decreased with increasing contrast. Only the gamma frequency recorded at the macroscale (i.e., MEG, which continued to increase at luminance contrast levels above 60%) was correlated with perceptual performance (Hadjipapas et al., 2015). This is an example of how temporal summation across a wide spatial distribution (reflected in MEG recordings) reflects different activity from spikes or the LFP. Finally, it is worth noting that the relationship between spatial integration across neurons, measured through correlation of spike counts between neurons, and EEG power has also been shown to be nonlinear, such that higher spike-count correlations predict high and low EEG amplitude, while low spike-count correlations are observed during time windows where intermediate EEG amplitudes are observed (Snyder et al., 2015).
In summary, although systematic relations exist between neural oscillations at different levels of observation, it is not advisable to test hypotheses regarding one level of observation by measuring at another level. Inter-scale interactions however provide a promising area of research for understanding the neuromechanistic role of neural oscillations. They also represent an important source of constraints for computational models of brain function, in turn to be tested by multi-scale empirical studies. Researchers studying macroscopic oscillations in humans may generate more precise, and more mechanistic hypotheses regarding these measurements when considering research at the micro- and mesoscale. Thus, by manipulating the nature of the stimulus, for example, its intensity or temporal frequency, specific mesoscopic circuits can be challenged and experimentally isolated, dramatically increasing the neurophysiological specificity of extracranial signals such as EEG or MEG. This technique is increasingly used and further emphasizes the benefits of developing hypotheses for human research based on the animal model. However, as is the case with the majority of imaging modalities (Boynton, 2011), not all robust and neurophysiologically meaningful metrics of oscillatory brain activity are linearly related to the behavioral indices measured in the same task. This long-standing conundrum in cognitive neuroscience research may also be explained by the non-overlap of processes observed at different spatial scales, further highlighting the importance of multi-scale studies.
## **3.7 Brain Oscillations and their Role in Behavior: A Conceptual Overview**
From its inception, the study of brain oscillations and their role in cognition has been multi-disciplinary, with a strong emphasis not only on physiological measurements, FROM NEURAL OSCILLATIONS TO COGNITIVE PROCESSES 49
but also on mathematical analysis and modeling, as well as behavioral observations. The resulting literature can be daunting for its extent, scope, and methodological complexity. Therefore, readers may benefit from a brief overview of key concepts, providing scaffolding for integrating current findings, and context for making sense of the wide range of theoretical notions related to oscillatory brain dynamics.
### **3.7.1 Hebbian Cell Assemblies and Brain Oscillations**
Adapting behavior based on experience is arguably one of the most essential functions of the human brain. Donald Hebb's (1949) classical theory in conjunction with theories of oscillatory brain activity are often used to account for this function. In these views, the brain's ability to form oscillatory networks comprising groups of neurons depends on a principle of association known as Hebb's second rule. This rule postulates that the synchronous activation of two cells or cell systems produces a facilitation of excitatory connections between them such that in the future activity of the one element produces a residual excitation of the other. A cell assembly refers to a distributed network of neurons that are bound together by the temporal synchronization of their sub-threshold membrane potentials and/or firing rates (Singer et al., 1990). Importantly, neuronal cell assemblies may be synchronized at local scales, separated in the millimeter range, but also at distances that span distinct cortical lobes (Pulvermuller & Fadiga, 2010). Theoretical and methodological advances in the neurosciences, including the discovery of long-term potentiation (Bliss & Lømo, 1973), whereby the responses of a post-synaptic cell are facilitated by oscillatory stimulation, have largely validated Hebb's notion, while also offering more detailed analyses of the physiological substrates that underlie the formation of oscillatory networks through experience (Nadel & Maurer, 2018).
Today, the ability of neurons to form networks based on coincidence of firing patterns can be explained at the molecular level (Andersen et al., 2017; Harris & Littleton, 2015), for example by reference to the unique properties of NMDA (N-Methyl-D-Aspartate) and AMPA (α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid) glutamate receptors (Henley & Wilkinson, 2016). Additional physiological mechanisms for coincidence-based network formation have been elucidated, such as the dual sensitivity of L-type calcium channels to back-propagating action potentials and pre-synaptic excitatory currents (Nanou & Catterall, 2018). Importantly, neuronal cell assemblies may be synchronized at local scales, separated in the millimeter range, but also at distances that span distinct cortical lobes. Hebb's original suggestion (1949) held that reverberating activity within cell assemblies constituted a transient percept or memory trace that can become more consolidated with the passage of time. The concept of reverberation, by providing a metaphorical notion of how oscillatory phenomena arise, has stimulated a large body of work, which in turn has identified a plethora of mechanisms for network organization and oscillatory brain activity, beyond temporal synchrony (Morone et al., 2017).
50 ANDREAS KEIL and NINA THIGPEN
### **3.7.2 Complex System Theory and Nonlinear Dynamics**
With the advent of powerful digital computers, conceptual frameworks that had been elusive because of their computational complexity, became increasingly popular. One group of concepts with strong implications for the study of oscillatory brain activity drew from theories of complex systems ("chaos theory") and nonlinear dynamics (Elbert et al., 1994). Applied to brain oscillations, these approaches describe fluctuations among different elements, often in so-called non-equilibrium conditions, where some form of energy or environmental constraint affects a complex, macroscopic system (Fuchs et al., 2000). Research conducted using this framework demonstrates that dynamics in complex systems may be characterized by the interaction of some quantifiable and continuous variable, and the effect that it exerts on the collective system state. In one flavor of nonlinear system research, the collective system state is measured by one dominant parameter, the order parameter, taken to index the high-level formulation of the system (Haken et al., 1985), whereas variables that can change the nature of the system dynamics are referred to as the "control parameter". When the control parameter reaches a particular value, the macroscopic system undergoes a phase transition and acquires a qualitatively novel set of properties. Once it is established, the new high-level order parameter may "enslave" the lower components—a phenomenon demonstrated in everyday life when the clapping of a large audience determines the clapping frequency of individual members in the audience.
Metrics of nonlinear dynamics such as largest Lyapunov coefficients or the Grassberger–Procaccia dimension (Elbert et al., 1994) have been used to characterize neural time series, aiming to capture dynamics above and beyond the periodic, sinewave-like, and stationary cycles that are assumed by linear methods such as the Fourier transform. In addition, approaches inspired by nonlinear systems research have made important contributions by emphasizing the role of oscillatory phase, and by providing tools for visualizing and analyzing nonlinear interactions among and between populations of neurons (Breakspear, 2017). Currently, some of these methods, such as phase space portraits, experience a renewed popularity and are applied in studies of motor preparation, perception, and awareness (Baria et al., 2017).
### **3.7.3 Spatio-Temporal Patterns and Travelling Waves**
Although oscillatory patterns are most easily visualized as changes in magnitude over time, researchers have recognized for a long time that the spatial dimension of oscillatory activity also plays a crucial role in characterizing oscillatory processes. Walter Freeman, one of the first researchers to explore this topic in depth, established a mathematical model in which spatio-temporal patterns consisting of mesoscopic "phase cones"—moving two-dimensional Gaussian fields with systematically changing FROM NEURAL OSCILLATIONS TO COGNITIVE PROCESSES 51
oscillatory phase—represent the nature of an odorant presented to the rabbit olfactory system (Freeman, 1991).
Current research has addressed this topic using refined mathematical tools and highresolution electrophysiological recordings. As a result, traveling oscillatory waves of neural activity have been found at many different frequencies, across wide spectrum of brain areas. Spreading over cortical or subcortical tissue as time passes, these waves have been related to many different behaviors, ranging from sensory to motor processing (Muller et al,, 2018).
### **3.7.4 Oscillatory Hierarchies**
Many prominent models of the functional role of oscillatory brain activity have considered interactions between oscillations at different temporal rates. A classical model of working memory proposed that hippocampal neurons encode memory content using timed gamma-frequency bursts, which in turn receive their temporal structure from the phase of low-frequency oscillations in the theta band (Lisman & Jensen, 2013). This account has received substantial support as well as extension and refinement based on computational and empirical studies.
In another widely recognized account, systematic relations across different frequencies are used by the brain to organize the interplay between behavioral and cognitive processes—the concept of "active sensing" emphasizes the active aspect of perceptual sampling (Schroeder et al., 2010). Examples for such active sensing include whisking and sniffing in rodents and saccadic sampling of visual scenes in primates. In all these cases, perception is tightly linked to the motor activity that causes the stimulation of sensory receptors as it initiates inflow of information through the sensory pathways. Each afferent volley of information meets ongoing brain states hypothesized to be partly determined by past experience and current goals, as well as the physiological properties of the tissue. In these hypothetical hierarchies, neural oscillations at lower frequencies (such as alpha or theta, 4–8 Hz as defined in adults) may provide temporal structure for higher-frequency phenomena, for example, beta- (13–30 Hz) or gammaband (>30 Hz) oscillations. In a similar vein, studies in macaque monkey visual cortex have suggested that high-amplitude gamma oscillations more likely occur during specific phases of the alpha cycle (Bonnefond & Jensen, 2015). These findings have been taken to indicate that alpha phase represents the excitability of the neural tissue, possibly aligning excitability of sensory cortices with other events such as expectancy or memory-driven signals (Kizuk & Mathewson, 2016; Mathewson et al., 2011).
### **3.7.5 Synchrony and Oscillatory Communication**
Most contemporary models of oscillatory brain activity emphasize the potential of rhythmic processes for organizing neural activity in time and space and thus for providing a mechanism for integrative coding across spatially separated units (neurons, 52 ANDREAS KEIL and NINA THIGPEN
columns, areas; Buzsáki & Draguhn, 2004). In earlier theories of oscillatory activity, temporal synchrony was seen as the crucial feature for coding information that belongs together but is distributed between different neurons or populations of neurons (von der Malsburg & Buhmann, 1992). This notion is readily aligned with the Hebbian perspective discussed earlier, adding to the appeal it has held for many decades. At the microscopic and mesoscopic level, synchronous firing in local circuits, especially in the gamma frequency range, has been proposed as a mechanism for cognitive processes as diverse as gestalt perception, predictive coding, motor preparation, and selective attention (Bauer et al., 2014; Keil et al., 2001).
Extending the concept of synchrony to long-range communication and integration, recent work focuses on the interaction between local and inter-area (long-range) synchrony, increasingly on oscillatory interactions across different frequencies (Chapter 20). For instance, oscillatory activity in the theta range (4–8 Hz) has been traditionally hypothesized as a potential mechanism for transmitting information between distant brain areas (Klimesch et al., 2005; Sarnthein et al., 1998). Empirical evidence in rodents, cats, and nonhuman primates supports this notion, with theta oscillations characterizing long-range signaling in large-scale networks, including the hippocampus, the amygdaloid, complex, and extensive cortical areas, during tasks that involve learning and memory (Popescu et al., 2009). Similar findings exist for alpha-band oscillations, discussed now as carriers of prediction signals from higher-order to sensory cortices. Importantly, the concept of synchrony in the context of these inter-area communications has been extended beyond zero-lag co-activation at different sites, and has instead identified inter-area interactions by the extent to which the phase lag between two recording sites is consistent over time, that is, so-called inter-site phase locking (Brovelli et al., 2004).
Together, local- and inter-area oscillations hold great promise for informing and constraining network-based models of human cognition. Because of their compatibility with findings obtained in the animal model, and the ability to relate neural activity across different levels of observation, indices of oscillatory brain activity also represent powerful dependent variables in cognitive neuroscience studies. The following example illustrate these benefits by selectively reviewing examples for such studies and address processes of perception, attention, learning, and memory.
## **3.8 Example 1: Alpha-Band Changes During Perception and Selective Attention**
As discussed, oscillatory activity in the alpha frequency band is typically observed during stimulus-absent conditions such as resting or sitting with the eyes closed (Berger, 1929; Pfurtscheller, 1989). Many early studies established the robust relationship between alpha power changes and perceptual tasks, demonstrating that high-alpha states tend to be blocked following events such as the opening of the eyes, the presentation FROM NEURAL OSCILLATIONS TO COGNITIVE PROCESSES 53
of a visual cue, or the direction of attention toward a salient visual stimulus (Adrian & Matthews, 1934; Klimesch, 1999; Pfurtscheller et al., 1996). Low levels of alpha power together with alpha phase also predict heightened performance in near-threshold detection tasks, where participants report weak sensory events (Mathewson et al., 2011; Weisz et al., 2014). This evidence supports a long-held notion that scalp-recorded alpha activity reflects a cortical state in which little sensory information is received (Pfurtscheller, 1992), mediated perhaps via a thalamic gating mechanism (Steriade et al., 1990).
Other findings are consistent with this notion.: Presenting a cue that directs attention to one hemifield prompts reduction of alpha power in the contralateral hemisphere (Foxe & Snyder, 2011). By contrast, alpha power over ipsilateral sensors (representing the ignored hemifield) remains stable (Thut et al., 2006), or increases (Kelly et al., 2006), taken to suggest suppression of irrelevant information. This interpretation is consistent with research examining attention to target items embedded in a rapid serial visual presentation stream of distractors. Accurate identification of rapidly presented targets amid non-targets is associated with higher pre-target alpha power (Petro & Keil, 2015). Thus, high alpha power may index behavioral states that benefit performance by reducing the processing of irrelevant sensory information (Klimesch et al., 2006). Importantly, these attention-related changes in alpha power are associated with faster and more accurate responses for the task, suggesting that they possess a functional role in the active selection of target stimulus features (Foxe & Snyder, 2011).
A further role of alpha oscillations during attention tasks is under consideration in the context of predictive coding. This has become a current topic in cognitive neuroscience. Increased alpha power and heightened inter-site phase-locking during target anticipation are proposed as a mechanism that optimizes the temporal organization of sensory processing and thus facilitates the sensory analysis of expected, task-relevant, visual stimuli (Samaha et al., 2015). Several of the different proposed functions of alphaband oscillations during perception and attention are not mutually exclusive and have given rise to the idea that the alpha frequency is used by a wide range of neural processes, in the service of different cognitive and behavioral goals (Chapter 10).
### **3.9 Example 2: Learning and Memory**
Work in the animal model abundantly demonstrates that associative learning induces Hebbian plasticity in widely distributed brain networks, both sub-cortical and cortical (Pape & Paré , 2010). These memory formation processes can be conceptualized as changes in the neural communication between nearby and distant brain loci, which dynamically sculpt neural signaling pathways at multiple levels of analysis. Recent findings suggest that neuronal oscillations are ideally suited to support the flexible formation of such network-level changes in neural architecture (Popescu et al., 2009), including those that support the acquisition and extinction of fear memories (Paré et al., 2002). In addition, computational models using simulated agents in artificial evolutionary environments show that network oscillations provide a fitness advantage, insofar as 54 ANDREAS KEIL and NINA THIGPEN
they help to promote rapid switches in perception and attention (Heerebout & Phaf, 2010). Oscillatory signals may therefore play an important role in the critical changes that occur when a previously innocuous stimulus acquires relevance for controlling behavior (Headley & Weinberger, 2011). At the level of neuronal populations, the associative principles that guide the formation of a newly acquired memory (e.g., the association between light and electric shock during classical fear conditioning) must effectively coordinate activity between neural representations of the conditioned stimuli (the light) and the systems that code biological value of the unconditioned event (the shock). Although conditioning-induced changes in neuroarchitecture and function occur on multiple spatio-temporal scales (Maren & Quirk, 2004), ranging from individual neurons to cortical sheets, and from minutes to days, the notion of a cell assembly (Hebb, 1949) provides the necessary conceptual framework for bridging across these multi-scale phenomena. Oscillatory synchronization between distributed neuronal assemblies in specific frequency bandwidths appears to represent a highly plausible substrate for synaptic plasticity transfer, that is, storing newly acquired memories as changes in synaptic weights (Paré et al., 2002). In particular, increased large-scale synchrony between subcortical and cortical networks may be crucial in producing the experience-dependent changes in the representation of fear-conditioned cues.
Another example is provided by a series of studies conducted by Walter Freeman and his colleagues (reviewed in Skarda & Freeman, 1987) in the olfactory system of the rabbit. The basic paradigm involves the placement of an 8 × 8 electrode grid onto the olfactory bulb in order to record electrocorticography (ECoG) signals associated with different odorant stimuli. To begin with, each odorant elicits a pattern of wave activity that appears as aperiodic noise with variability across trials. However, after the animal learns to associate an odor with a motivationally relevant outcome, for example, the delivery of food or aversive tactile stimulation, neural activity at the olfactory bulb undergoes a state transition whereby the odor comes to elicit a discriminant spatiotemporal pattern of amplitude across the electrode grid array. The learning-related establishment of a new global response pattern then acts to enslave the output of individual neurons (Freeman, 1994). Freeman interprets such selective changes in spatiotemporal amplitude as embodying the affective meaning of a stimulus for the animal, with meaning changing in accordance with the momentary relevance of a stimulus (e.g., an animal responds differently to an odorant associated with food once it is fed to satiety). A mechanism for stimulus selective changes in the output of olfactory neurons is provided by alterations of synaptic efficiency and neuropil structure, guided by Hebbian principles of association.
## **3.10 Example 3: Generating Brain Oscillations by Periodic Stimulation**
Rhythmic modulation of stimulus contrast or luminance at a constant rate over a period of time evokes oscillatory field responses in the visual cortex at the same frequency FROM NEURAL OSCILLATIONS TO COGNITIVE PROCESSES 55
as the modulation rate of the stimulus, often including higher harmonics—integer multiples of the stimulation frequency. The harmonic responses depend on the duty cycle, the stimulation method, and the complexity of the stimulus array (Norcia et al., 2015). In the visual domain, large-scale frequency-following responses evoked by periodic stimulation are referred to as steady-state visual evoked potentials (ssVEPs). These driven oscillations are best quantified in the frequency or the time-frequency-domain, where they can be reliably separated from noise and quantified as the spectral power in a narrow frequency range. Several studies have demonstrated that the flicker-evoked ssVEP is predominantly generated in the primary visual and to some extent in adjacent, higher order, cortices (Müller et al., 1997; Wieser & Keil, 2011). Interestingly, a number of studies have suggested different neural sources for the fundamental frequency and the higher harmonics, although these findings await replication and further interpretation (Kim et al., 2010). Generally, the ssVEP can easily be driven in lower-tier (retinotopic) visual cortices using high-contrast luminance modulation governed by a rapid squarewave (on-off) stimulation. For studies of higher-order cognitive processes, however, researchers may periodically modulate specific stimulus dimensions other than luminance or contrast, while holding these lower-level properties constant (or varying them randomly). Such an approach evokes ssVEPs in brain areas sensitive to the particular feature or stimulus dimension of interest (Giabbiconi et al., 2016; McTeague et al., 2015). For example, stimulation techniques have been used that isolate the ssVEP response to face identity generated in higher order visual areas such as the fusiform cortex (Rossion & Boremanse, 2011).
A related issue often discussed in the context of driven oscillations is the question to what extent ssVEPs can be regarded as a linear superposition of transient ERPs, or alternatively represent a nonlinear response that possesses properties beyond the linear combination of individual brain responses (Capilla et al., 2011; Regan, 1989). A similar current debate exists between the view that driven oscillations represent a temporal alignment or "entrainment" of oscillations that are already present spontaneously, and the alternative view that driven oscillations represent newly shaped waveforms, on top of ongoing oscillations (Keitel et al., 2019). Initial studies in the field have argued that observing higher harmonics when using harmonically simple (e.g., sinusoidal) modulation of luminance or contrast is considered evidence of nonlinearity, thus providing evidence for perspectives emphasizing resonance and entrainment (Regan, 1989). Subsequent work has examined the extent to which ssVEPs can be explained by properties of transient ERPs, and has observed that especially with square wave (onoff) modulation, ssVEPs may be modeled by transient ERP features with satisfactory accuracy (Capilla et al., 2011), providing evidence for a superposition perspective. The interpretation of these findings is not straightforward, however, because transient brain responses themselves represent a combination of individual trials that vary greatly in latency (phase) and amplitude, limiting their use for unambiguously explaining the generating mechanism underlying ssVEPs. In line with this notion, other studies have reported that the ssVEP amplitude is poorly predicted by single-trial power changes at the driving frequency, but is best predicted by locking of the single-trial phase with
56 ANDREAS KEIL and NINA THIGPEN
**Figure 3.3** Effects of stimulus intensity on inter-trial phase locking of driven oscillations. Participants viewed sinusoidal gratings flickering at 15 Hz. Gratings varied in luminance, with 40 low-luminance trials (.4 cd/m2), 40 medium-luminance trials (4.9 cd/m2), and 40 high-luminance trials (70.7 cd/m2). Each colored line represents one single trial from sensor Oz. Inter-trial phase locking increases with increasing luminance, whereas the overall magnitude of the signal within the single trials does not change. The increased phase-locking is associated with increases in 15-Hz power of the trial-averaged signal, as depicted in the topographies shown on the right.Data from Thigpen et al., 2018.
the driving stimulus across trials (Moratti et al., 2007). Figure 3.3 shows an example of this phenomenon as it interacts with stimulus intensity, demonstrating increasing phase alignment of single trial EEG traces with increasing stimulus contrast. The debate of entrainment versus superposition perspectives is ongoing, and ssVEPs (because of their known frequency and pronounced signal) are well suited for examining competing hypotheses regarding the interaction of ongoing oscillations and sensory events.
## **3.11 Conclusions and Outlook: Elements of a Conceptual Framework of Oscillatory Brain Activity**
This chapter aimed to illustrate how studies of oscillatory brain activity provide rich opportunity for testing hypotheses relating brain function to cognitive processes. Measuring oscillatory activity during cognitive task performance opens avenues into developing and testing neuromechanistic accounts of some of the most central building blocks of human behavior and experience. In conclusion, we discuss challenges for this field moving forward, and provide key concepts towards an integrative framework of oscillatory brain activity in the study of cognition.
FROM NEURAL OSCILLATIONS TO COGNITIVE PROCESSES 57
### **3.11.1 Oscillations as Epiphenomena, and Other Challenges**
A long-standing debate in the field centers around the question to what extent brain oscillations possess a primary functional role, as opposed to arising from other nonoscillatory processes as a by-product, or epiphenomenon (Buzsáki & Draguhn, 2004). For example, does a spike burst represent an oscillation, or a mere sequence of individual events? The question of functional relevance has been difficult to address because the required ground truth, for example, "there is an oscillation at 11.5 Hz", is often something the researcher wishes to establish, rather than something that can be used as a premise. Current research leverages causal manipulations such as electric micro-stimulation in experimental animals, synchronized to the phase of ongoing oscillations to determine if altering a robustly measured ongoing oscillation affects the animal's behavior in a systematic fashion (Tehovnik et al., 2006). Such data, challenging to obtain because it requires predicting the phase of the oscillatory signal over time, would present direct evidence supporting a causal role of oscillatory activity. Other approaches underway in several laboratories use similar causal manipulation, as well as driven oscillations, to address this question.
Additional challenges for researchers using metrics of oscillatory activity are rooted in the fact that highly complex data arrays that may contain sensors, conditions, time points, trials, etc., tend to get further inflated when adding a frequency dimension. This triggered attempts towards using multivariate methods, machine learning methods, or other approaches, all aiming at reducing the dimensionality of the data without losing information that is relevant to addressing the empirical question of interest]. The resulting methodological diversity has not only been enriching for the field, but also often prevented direct comparisons of results from different laboratories, and thus has been regarded as one obstacle towards reproducing and replicating findings. Ongoing efforts to improve the training of next-generation researchers are expected to address this issue, by adding computer science, digital signal processing, and advanced statistics to undergraduate and graduate curricula. Current trends of expressing hypotheses in terms of mathematical models that can be explicitly tested and gradually improved are crucial in this respect and are readily applied to indices of oscillatory brain activity. As with many other fields in the biomedical sciences, (re-)establishing a culture of knowing the history of the field, of systematic and programmatic research, and of applying rigorous methods is an obvious goal in research on brain oscillations. The following key concepts summarize areas of conceptual progress in the field and provide avenues for future research.
### **3.11.2 Oscillations as Drivers of Plasticity**
Brain oscillations are widely considered reflections of network activity, but growing support is also evident for their role in mediating neuroplastic changes that result in 58 ANDREAS KEIL and NINA THIGPEN
the *formation* of networks, local and distributed. The high signal-to-noise ratio of many frequency-domain measures and the resulting potential for trial-by-trial analyses may be leveraged to quantify neural changes that occur over the course of an experimental session (McTeague et al., 2015). Such an approach complements trial averaging, which is still the dominant approach in cognitive neuroscience, and sheds light on adaptation dynamics and plasticity in response to the experimental situation, processes of high ecological validity and with substantial clinical relevance.
### **3.11.3 Oscillations as Pacemakers for Cognition and Behavior**
A substantial body of research addresses the role of low-frequency oscillatory brain activity for embedding and organizing neural, cognitive, and motor processes. Cornerstone results from this line of research include that perceptual and motor performance varies in a rhythmic fashion: recurrent time windows exist, in which cognition and motor action can be optimally initiated and executed, interspersed with time windows of reduced performance (VanRullen, 2016). Relating these behavioral rhythms to brain oscillations holds promise for advancing models of the temporal organization of cognitive processing.
### **3.11.4 Oscillations as Carriers of Communication Signals**
Several chapters in this volume address the potential of oscillatory activity in lowerfrequency bands such as alpha or theta for integrating information in space, and for mediating the neural communication between units, local and distal (Chapters 9, 10, and 20). Establishing the functional role of oscillatory phenomena in neural communication, across levels of observation, will greatly benefit from emerging multimodal and multi-species methods, including new recording and stimulation techniques, well suited to cross-validate observations and combine measurement and stimulation approaches (Adesnik, 2018).
### **3.11.5 Oscillations as Organizing Principles for Regulating Complex System States**
From a perspective of complex systems, a major function of brain oscillations lies in representing macroscopic states that emerge from systematic nonlinear interactions between units at the microscopic and mesoscopic level. Increasingly, computational models exist, which make quantitative predictions for how these different levels interact. For example, in-silico studies have leveraged the steady increase in computing capacity FROM NEURAL OSCILLATIONS TO COGNITIVE PROCESSES 59
to offer alternative models of inter-scale nonlinear interactions, which may provide critical predictions to be tested in empirical work (Neymotin et al., 2013).
### **3.11.6 Oscillations as Substrate of Representations in Perception and Memory**
Finally, oscillations have been long regarded as a candidate mechanism for coding percepts and memories. As discussed, oscillatory dynamics provide a unifying way for describing diverse mechanisms involved in these cognitive processes, including the spatio-temporal dynamics and plastic changes within and between neuronal ensembles. They offer a parsimonious account for integrating activity across distributed functional units without invoking the widely criticized top-down versus bottom-up dichotomy (Awh et al., 2012). Current developments in cognitive science and experimental psychology to increasingly rely on computational modeling will facilitate the integration of experimental observations from the level of brain oscillations to the level of task performance.
In summary, brain oscillations have opened exciting new avenues in the study of cognitive and behavioral processes. Beyond mere measurements of power in a specific frequency band, recent developments have provided the research community with tools that allow us to visualize the dynamic interplay among different frequencies, quantify the role of phase in coding information, and assess the rhythmic interactions between distal brain areas. Together with rapid theoretical and computational advances, these tools will continue to provide unique insights into brain systems dynamics and their relation to behavior and experience.
### **References**
- Adesnik, H. (2018). Cell type-specific optogenetic dissection of brain rhythms. *Trends in Neurosciences*, *41*(3), 122–124.
- Adrian, E. D. & Matthews, B. H. (1934). The Berger rhythm: Potential changes from the occipital lobes in man. *Brain*, *57*(4), 355–385.
- Andersen, N., Krauth, N., & Nabavi, S. (2017). Hebbian plasticity in vivo: Relevance and induction. *Current Opinion in Neurobiology*, *45*, 188–192. [https://doi.org/10.1016/](https://doi.org/10.1016/j.conb.2017.06.001) [j.conb.2017.06.001](https://doi.org/10.1016/j.conb.2017.06.001)
- Awh, E., Belopolsky, A. V., & Theeuwes, J. (2012). Top-down versus bottom-up attentional control: A failed theoretical dichotomy. *Trends in Cognitive Sciences*, *16*(8), 437–443. [https://doi.](https://doi.org/10.1016/J.Tics.2012.06.010) [org/10.1016/J.Tics.2012.06.010](https://doi.org/10.1016/J.Tics.2012.06.010)
- Baria, A. T., Maniscalco, B., & He, B. J. (2017). Initial-state-dependent, robust, transient neural dynamics encode conscious visual perception. *PLOS Computational Biology*, *13*(11), e1005806.
- Başar, E. & Güntekin, B. (2012). A short review of alpha activity in cognitive processes and in cognitive impairment. *International Journal of Psychophysiology*, *86*(1), 25–38. [https://doi.](https://doi.org/10.1016/j.ijpsycho.2012.07.001) [org/10.1016/j.ijpsycho.2012.07.001](https://doi.org/10.1016/j.ijpsycho.2012.07.001)
60 ANDREAS KEIL and NINA THIGPEN
- Bauer, M., Stenner, M.-P., Friston, K. J., & Dolan, R. J. (2014). Attentional modulation of alpha/ beta and gamma oscillations reflect functionally distinct processes. *Journal of Neuroscience*, *34*(48), 16117–16125.
- Berger, H. (1929). Über das Elektrenkephalogramm des Menschen. *Archiv Für Psychiatrie Und Nervenkrankheiten*, *87*, 527–570.
- Bernstein, J. (1868). Ueber den zeitlichen Verlauf der negativen Schwankung des Nervenstroms. *Archiv für die gesamte Physiologie des Menschen und der Tiere*, *1*(1), 173–207. [https://doi.org/](https://doi.org/10.1007/BF01640316) [10.1007/BF01640316](https://doi.org/10.1007/BF01640316)
- Bliss, T. V. P. & Lømo, T. (1973). Long-lasting potentiation of synaptic transmission in the dentate area of the anaesthetized rabbit following stimulation of the perforant path. *The Journal of Physiology*, *232*(2), 331–356.
- Bonnefond, M. & Jensen, O. (2015). Gamma activity coupled to alpha phase as a mechanism for top-down controlled gating. *PLOS ONE*, *10*(6), e0128667. [https://doi.org/10.1371/journal.](https://doi.org/10.1371/journal.pone.0128667) [pone.0128667](https://doi.org/10.1371/journal.pone.0128667)
- Boynton, G. M. (2011). Spikes, BOLD, attention, and awareness: A comparison of electrophysiological and fMRI signals in V1. *Journal of Vision*, *11*(5), 12–12. [https://doi.org/10.1167/](https://doi.org/10.1167/11.5.12) [11.5.12](https://doi.org/10.1167/11.5.12)
- Breakspear, M. (2017). Dynamic models of large-scale brain activity. *Nature Neuroscience*, *20*(3), 340–352.
- Brovelli, A., Ding, M., Ledberg, A., Chen, Y., Nakamura, R., & Bressler, S. L. (2004). Beta oscillations in a large-scale sensorimotor cortical network: directional influences revealed by Granger causality. *Proceedings of the National Academy of Sciences of the United States of America*, *101*(26), 9849–9854. (15210971).
- Buzsáki, G., Anastassiou, C. A., & Koch, C. (2012). The origin of extracellular fields and currents—EEG, ECoG, LFP and spikes. *Nature Reviews Neuroscience*, *13*(6), 407–420.
- Buzsáki, G. & Draguhn, A. (2004). Neuronal oscillations in cortical networks. *Science*, *304*(5679), 1926–1929.
- Buzsáki, G., Logothetis, N., & Singer, W. (2013). Scaling brain size, keeping timing: Evolutionary preservation of brain rhythms. *Neuron*, *80*(3), 751–764. [https://doi.org/10.1016/j.neu](https://doi.org/10.1016/j.neuron.2013.10.002) [ron.2013.10.002](https://doi.org/10.1016/j.neuron.2013.10.002)
- Capilla, A., Pazo-Alvarez, P., Darriba, A., Campo, P., & Gross, J. (2011). Steady-state visual evoked potentials can be explained by temporal superposition of transient event-related responses. *PLoS One*, *6*(1), e14543.
- Cohen, M. X. (2014). *Analyzing neural time series data: Theory and practice*. MIT Press.
- Donner, T. H. & Siegel, M. (2011). A framework for local cortical oscillation patterns. *Trends in Cognitive Sciences*, *15*(5), 191–199.
- Elbert, T., Ray, W. J., Kowalik, Z. J., Skinner, J. E., Graf, K. E., & Birbaumer, N. (1994). Chaos and physiology: Deterministic chaos in excitable cell assemblies. *Physiology Review*, *74*(1), 1–47.
- Foxe, J. J. & Snyder, A. C. (2011). The role of alpha-band brain oscillations as a sensory suppression mechanism during selective attention. *Frontiers in Psychology*, *2*, 154. [https://](https://doi.org/10.3389/fpsyg.2011.00154) [doi.org/10.3389/fpsyg.2011.00154](https://doi.org/10.3389/fpsyg.2011.00154)
- Freeman, W. J. (1991). The physiology of perception. *Scientific American*, *264*, 78–87.
- Freeman, W. J. (1994). Role of chaotic dynamics in neural plasticity. *Progress in Brain Research*, *102*, 319–333.
FROM NEURAL OSCILLATIONS TO COGNITIVE PROCESSES 61
- Fuchs, A., Jirsa, V. K., & Kelso, J. A. (2000). Theory of the relation between human brain activity (MEG) and hand movements. *Neuroimage*, *11*(5 Pt 1), 359–369. [https://doi.org/10.1006/](https://doi.org/10.1006/nimg.1999.0532) [nimg.1999.0532](https://doi.org/10.1006/nimg.1999.0532)
- Galambos, R. (1992). A comparison of certain gamma-band (40 Hz) brain rhythms in cat and man. In E. Basar & T. Bullock (Eds.), *Induced rhythms in the brain* (pp. 103–122). Springer.
- Giabbiconi, C.-M., Jurilj, V., Gruber, T., & Vocks, S. (2016). Steady-state visually evoked potential correlates of human body perception. *Experimental Brain Research*, *234*(11),1–11. [https://](https://doi.org/10.1007/s00221-016-4711-8) [doi.org/10.1007/s00221-016-4711-8](https://doi.org/10.1007/s00221-016-4711-8)
- Gütig, R. (2014). To spike, or when to spike? *Current Opinion in Neurobiology*, *25*, 134–139.
- Hadjipapas, A., Lowet, E., Roberts, M. J., Peter, A., & De Weerd, P. (2015). Parametric variation of gamma frequency and power with luminance contrast: A comparative study of human MEG and monkey LFP and spike responses. *NeuroImage*, *112*, 327–340. [https://doi.org/](https://doi.org/10.1016/j.neuroimage.2015.02.062) [10.1016/j.neuroimage.2015.02.062](https://doi.org/10.1016/j.neuroimage.2015.02.062)
- Haken, H., Kelso, J. A., & Bunz, H. (1985). A theoretical model of phase transitions in human hand movements. *Biological Cybernetics*, *51*(5), 347–356.
- Harris, K. P. & Littleton, J. T. (2015). Transmission, development, and plasticity of synapses. *Genetics*, *201*(2), 345–375.
- Headley, D. B. & Weinberger, N. M. (2011). Gamma-band activation predicts both associative memory and cortical plasticity. *Journal of Neuroscience*, *31*(36), 12748–12758. [https://doi.org/](https://doi.org/10.1523/JNEUROSCI.2528-11.2011) [10.1523/JNEUROSCI.2528-11.2011](https://doi.org/10.1523/JNEUROSCI.2528-11.2011)
- Hebb, D. (1949). *The organization of behavior: A neuropsychological theory*. Wiley.
- Heerebout, B. T. & Phaf, R. H. (2010). Good vibrations switch attention: An affective function for network oscillations in evolutionary simulations. *Cognitive, Affective, & Behavioral Neuroscience*, *10*(2), 217–229.
- Henley, J. M. & Wilkinson, K. A. (2016). Synaptic AMPA receptor composition in development, plasticity and disease. *Nature Reviews Neuroscience*, *17*(6), 337–350. [https://doi.org/](https://doi.org/10.1038/nrn.2016.37) [10.1038/nrn.2016.37](https://doi.org/10.1038/nrn.2016.37)
- Herrmann, C. S., Strüber, D., Helfrich, R. F., & Engel, A. K. (2016). EEG oscillations: From correlation to causality. *International Journal of Psychophysiology*, *103*, 12–21. [https://doi.org/](https://doi.org/10.1016/j.ijpsycho.2015.02.003) [10.1016/j.ijpsycho.2015.02.003](https://doi.org/10.1016/j.ijpsycho.2015.02.003)
- Keil, A., Gruber, T., & Muller, M. M. (2001). Functional correlates of macroscopic highfrequency brain activity in the human visual system. *Neuroscience and Biobehavioral Reviews*, *25*(6), 527–534.
- Keitel, C., Keitel, A., Benwell, C. S. Y., Daube, C., Thut, G., & Gross, J. (2019). Stimulus-driven brain rhythms within the alpha band: The attentional-modulation conundrum. *Journal of Neuroscience*, *39*(16), 3119–3129.
- Kelly, S. P., Lalor, E. C., Reilly, R. B., & Foxe, J. J. (2006). Increases in alpha oscillatory power reflect an active retinotopic mechanism for distracter suppression during sustained visuospatial attention. *Journal of Neurophysiology*, *95*(6), 3844–3851. [https://doi.org/10.1152/](https://doi.org/10.1152/jn.01234.2005) [jn.01234.2005](https://doi.org/10.1152/jn.01234.2005)
- Kim, Y.-J., Grabowecky, M., Paller, K. A., & Suzuki, S. (2010). Differential roles of frequency-following and frequency-doubling visual responses revealed by evoked neural harmonics. *Journal of Cognitive Neuroscience*, *23*(8), 1875–1886. [https://doi.org/10.1162/](https://doi.org/10.1162/jocn.2010.21536) [jocn.2010.21536](https://doi.org/10.1162/jocn.2010.21536)
62 ANDREAS KEIL and NINA THIGPEN
- Kizuk, S. A. D. & Mathewson, K. E. (2016). Power and phase of alpha oscillations reveal an interaction between spatial and temporal visual attention. *Journal of Cognitive Neuroscience*, *29*(3), 480–494. [https://doi.org/10.1162/jocn\\_a\\_01058](https://doi.org/10.1162/jocn_a_01058)
- Klimesch, W. (1999). EEG alpha and theta oscillations reflect cognitive and memory performance: A review and analysis. *Brain Research Reviews*, *29*(2), 169–195. [https://doi.org/10.1016/](https://doi.org/10.1016/S0165-0173(98)00056-3) [S0165-0173\(98\)00056-3](https://doi.org/10.1016/S0165-0173(98)00056-3)
- Klimesch, W., Sauseng, P., & Hanslmayr, S. (2006). EEG alpha oscillations: The inhibitiontiming hypothesis. *Brain Research Reviews*, *53*(1), 63–88.
- Klimesch, W., Schack, B., & Sauseng, P. (2005). The functional significance of theta and upper alpha oscillations. *Experimental Psychology*, *52*(2), 99–108.
- Lisman, J. E., & Jensen, O. (2013). The theta-gamma neural code. *Neuron*, *77*(6), 1002–1016.
- Lopes da Silva, F. (1991). Neural mechanisms underlying brain waves: from neural membranes to networks. *Electroencephalography and Clinical Neurophysiology*, *79*(2), 81–93. [https://doi.](https://doi.org/10.1016/0013-4694(91)90044-5) [org/10.1016/0013-4694\(91\)90044-5](https://doi.org/10.1016/0013-4694(91)90044-5)
- Maren, S. & Quirk, G. J. (2004). Neuronal signalling of fear memory. *Nature Reviews Neuroscience*, *5*(11), 844–852.
- Marrazzi, A. S. & Lorente de No, R. (1944). Interaction of neighboring fibres in myelinated nerve. *Journal of Neurophysiology*, *7*(2), 83–101.
- Mathewson, K. E., Lleras, A., Beck, D. M., Fabiani, M., Ro, T., & Gratton, G. (2011). Pulsed out of awareness: EEG alpha oscillations represent a pulsed-inhibition of ongoing cortical processing. *Frontiers in Psychology*, *2*, 99.
- Mazzoni, A., Whittingstall, K., Brunel, N., Logothetis, N. K., & Panzeri, S. (2010). Understanding the relationships between spike rate and delta/gamma frequency bands of LFPs and EEGs using a local cortical network model. *NeuroImage*, *52*(3), 956–972. [https://](https://doi.org/10.1016/j.neuroimage.2009.12.040) [doi.org/10.1016/j.neuroimage.2009.12.040](https://doi.org/10.1016/j.neuroimage.2009.12.040)
- McTeague, L. M., Gruss, L. F., & Keil, A. (2015). Aversive learning shapes neuronal orientation tuning in human visual cortex. *Nature Communications*, *6*, 7823. [https://doi.org/10.1038/nco](https://doi.org/10.1038/ncomms8823) [mms8823](https://doi.org/10.1038/ncomms8823)
- Moon, J.-Y., Lee, U., Blain-Moraes, S., & Mashour, G. A. (2015). General relationship of global topology, local dynamics, and directionality in large-scale brain networks. *PLoS Computational Biology*, *11*(4), e1004225.
- Moratti, S., Clementz, B. A., Gao, Y., Ortiz, T., & Keil, A. (2007). Neural mechanisms of evoked oscillations: stability and interaction with transient events. *Human Brain Mapping*, *28*(12), 1318–1333.
- Morone, F., Roth, K., Min, B., Stanley, H. E., & Makse, H. A. (2017). Model of brain activation predicts the neural collective influence map of the brain. *Proceedings of the National Academy of Sciences of the United States of America*, *114*(15), 3849–3854. [https://doi.org/](https://doi.org/10.1073/pnas.1620808114) [10.1073/pnas.1620808114](https://doi.org/10.1073/pnas.1620808114)
- Muller, L., Chavane, F., Reynolds, J., & Sejnowski, T. J. (2018). Cortical travelling waves: mechanisms and computational principles. *Nature Reviews Neuroscience*, *19*(5), 255– 268.
- Müller, M. M., Teder, W., & Hillyard, S. A. (1997). Magnetoencephalographic recording of steady-state visual evoked cortical activity. *Brain Topography*, *9*(3), 163–168.
- Nadel, L. & Maurer, A. P. (2018). Recalling Lashley and reconsolidating Hebb. *Hippocampus*, *0*(0), 1–18.
FROM NEURAL OSCILLATIONS TO COGNITIVE PROCESSES 63
- Nanou, E. & Catterall, W. A. (2018). Calcium channels, synaptic plasticity, and neuropsychiatric disease. *Neuron*, *98*(3), 466–481.
- Naze, S., Bernard, C., & Jirsa, V. (2015). Computational modeling of seizure dynamics using coupled neuronal networks: Factors shaping epileptiform activity. *PLoS Computational Biology*, *11*(5), e1004209.
- Neymotin, S. A., Hilscher, M. M., Moulin, T. C., Skolnick, Y., Lazarewicz, M. T., & Lytton, W. W. (2013). *Ih* tunes theta/gamma oscillations and cross-frequency coupling in an *in silico* CA3 model. *PLoS One*, *8*(10), e76285.
- Norcia, A. M., Appelbaum, L. G., Ales, J. M., Cottereau, B. R., & Rossion, B. (2015). The steadystate visual evoked potential in vision research: A review. *Journal of Vision*, *15*(6), 4–4.
- Nunez, P. L., & Srinivasan, R. (2006). *Electric fields of the brain* (2nd ed.). Oxford University Press.
- Olejniczak, P. (2006). Neurophysiologic basis of EEG. *Journal of Clinical Neurophysiology*, *23*(3), 186–189.
- Osipova, D., Hermes, D., & Jensen, O. (2008). Gamma power is phase-locked to posterior alpha activity. *PLoS One*, *3*(12), e3990.
- Pape, H.-C., & Paré, D. (2010). Plastic synaptic networks of the amygdala for the acquisition, expression, and extinction of conditioned fear. *Physiological Reviews*, *90*(2), 419–463. [https://](https://doi.org/10.1152/physrev.00037.2009) [doi.org/10.1152/physrev.00037.2009](https://doi.org/10.1152/physrev.00037.2009)
- Paré, D., Collins, D. R., & Pelletier, J. G. (2002). Amygdala oscillations and the consolidation of emotional memories. *Trends in Cognitive Sciences*, *6*(7), 306–314. [https://doi.org/10.1016/](https://doi.org/10.1016/S1364-6613(02)01924-1) [S1364-6613\(02\)01924-1](https://doi.org/10.1016/S1364-6613(02)01924-1)
- Parvizi, J. & Kastner, S. (2018). Promises and limitations of human intracranial electroencephalography. *Nature Neuroscience*, *21*(4), 474.
- Petro, N. M. & Keil, A. (2015). Pre-target oscillatory brain activity and the attentional blink. *Experimental Brain Research*, *233*(12), 3583–3595.
- Pfurtscheller, G. (1989). Spatiotemporal analysis of alpha frequency components with the ERD technique. *Brain Topography*, *2*(1–2), 3–8.
- Pfurtscheller, G. (1992). Event-related synchronization (ERS): An electrophysiological correlate of cortical areas at rest. *Electroencephalography and Clinical Neurophysiology*, *83*, 62–69.
- Pfurtscheller, G., Stancak, A., Jr., & Neuper, C. (1996). Event-related synchronization (ERS) in the alpha band--an electrophysiological correlate of cortical idling: A review. *International Journal of Psychophysiology*, *24*(1–2), 39–46.
- Poldrack, R. A. (2011). Inferring mental states from neuroimaging data: From reverse inference to large-scale decoding. *Neuron*, *72*(5), 692–697.
- Popescu, A. T., Popa, D., & Paré, D. (2009). Coherent gamma oscillations couple the amygdala and striatum during learning. *Nature Neuroscience*, *12*(6), 801–807. [https://doi.org/10.1038/](https://doi.org/10.1038/nn.2305) [nn.2305](https://doi.org/10.1038/nn.2305)
- Pulvermuller, F., & Fadiga, L. (2010). Active perception: Sensorimotor circuits as a cortical basis for language. *Nature Reviews Neuroscience*, *11*(5), 351–360. [https://doi.org/10.1038/](https://doi.org/10.1038/nrn2811) [nrn2811](https://doi.org/10.1038/nrn2811)
- Regan, D. (1989). *Human brain electrophysiology: Evoked potentials and evoked magnetic fields in science and medicine*. Elsevier.
- Rossion, B., & Boremanse, A. (2011). Robust sensitivity to facial identity in the right human occipito-temporal cortex as revealed by steady-state visual-evoked potentials. *Journal of Vision*, *11*(2), 16.
64 ANDREAS KEIL and NINA THIGPEN
- Samaha, J., Bauer, P., Cimaroli, S., & Postle, B. R. (2015). Top-down control of the phase of alpha-band oscillations as a mechanism for temporal prediction. *Proceedings of the National Academy of Sciences*, *112*(27), 8439–8444.
- Sarnthein, J., Petsche, H., Rappelsberger, P., Shaw, G. L., & von Stein, A. (1998). Synchronization between prefrontal and posterior association cortex during human working memory. *Proceeding of the National Academy of Sciences of the United States of America*, *95*(12), 7092–7096.
- Schroeder, C. E., & Lakatos, P. (2009). Low-frequency neuronal oscillations as instruments of sensory selection. *Trends in Neuroscience*, *32*(1), 9–18.
- Schroeder, C. E., Wilson, D. A., Radman, T., Scharfman, H., & Lakatos, P. (2010). Dynamics of active sensing and perceptual selection. *Current Opinion in Neurobiology*, *20*(2), 172–176.
- Singer, W., Gray, C., Engel, A., König, P., Artola, A., & Brocher, S. (1990). Formation of cortical cell assemblies. *Cold Spring Harbor Symposium on Quantitative Biology*, *55*, 939–952.
- Skarda, C. A., & Freeman, W. J. (1987). How brains make chaos in order to make sense of the world. *Behavioral and Brain Sciences*, *10*(2), 161–173. [https://doi.org/10.1017/S0140525X0](https://doi.org/10.1017/S0140525X00047336) [0047336](https://doi.org/10.1017/S0140525X00047336)
- Snyder, A. C., Morais, M. J., Willis, C. M., & Smith, M. A. (2015). Global network influences on local functional connectivity. *Nature Neuroscience*, *18*(5), 736–743. [https://doi.org/10.1038/](https://doi.org/10.1038/nn.3979) [nn.3979](https://doi.org/10.1038/nn.3979)
- Steriade, M., Gloor, P., Llinás, R. R., Lopes da Silva, F. H., & Mesulam, M.-M. (1990). Basic mechanisms of cerebral rhythmic activities. *Electroencephalography and Clinical Neurophysiology*, *76*(6), 481–508. [https://doi.org/10.1016/0013-4694\(90\)90001-Z](https://doi.org/10.1016/0013-4694(90)90001-Z)
- Tehovnik, E. J., Tolias, A. S., Sultan, F., Slocum, W. M., & Logothetis, N. K. (2006). Direct and indirect activation of cortical neurons by electrical microstimulation. *Journal of Neurophysiology*, *96*(2), 512–521.
- Thigpen, N. N., Bradley, M. M., & Keil, A. (2018). Assessing the relationship between pupil diameter and visuocortical activity. *Journal of Vision*, *18*(6), 7–7.
- Thut, G., Nietzel, A., Brandt, S. A., & Pascual-Leone, A. (2006). Alpha-band electroencephalographic activity over occipital cortex indexes visuospatial attention bias and predicts visual target detection. *Journal of Neuroscience*, *26*(37), 9494–9502.
- VanRullen, R. (2016). Perceptual cycles. *Trends in Cognitive Sciences*, *20*(10), 723–735. [https://](https://doi.org/10.1016/j.tics.2016.07.006) [doi.org/10.1016/j.tics.2016.07.006](https://doi.org/10.1016/j.tics.2016.07.006)
- von der Malsburg, C. & Buhmann, J. (1992). Sensory segmentation with coupled neural oscillators. *Biological Cybernetics*, *67*(3), 233–242.
- Weisz, N., Wühle, A., Monittola, G., Demarchi, G., Frey, J., Popov, T., & Braun, C. (2014). Prestimulus oscillatory power and connectivity patterns predispose conscious somatosensory perception. *Proceedings of the National Academy of Sciences*, *111*(4), E417–E425. [https://](https://doi.org/10.1073/pnas.1317267111) [doi.org/10.1073/pnas.1317267111](https://doi.org/10.1073/pnas.1317267111)
- Wieser, M. J. & Keil, A. (2011). Temporal trade-off effects in sustained attention: Dynamics in visual cortex predict the target detection performance during distraction. *Journal of Neuroscience*, *31*(21), 7784–7790.
- Yuval-Greenberg, S., Tomer, O., Keren, A. S., Nelken, I., & Deouell, L. Y. (2008). Transient induced gamma-band response in EEG as a manifestation of miniature saccades. *Neuron*, *58*(3), 429–441.
# [CHAPTER 4](#page-5-6)
# [TIME-FREQUENCY](#page-5-6) [DECOMP OSITION METHODS](#page-5-6) [FOR EVENT-REL ATED](#page-5-6) [POTENTIAL ANALYSIS](#page-5-6)
SELIN AVIYENTE
### **4.1 Introduction**
EEG reflects the electrical activity of a collection of neural populations in the brain. As such, it reflects the superposition of different simultaneously acting dynamical systems. When a large number of parallel-oriented cortical neurons receive the same repetitive synaptic input, their synchronous activity produces extracellular rhythmic field potentials. These electrical fields are volume conducted throughout the brain and recorded as EEG from the scalp (Nunez & Srinivasan, 2006). In recent years, it has been suggested that this synchronization optimizes relations between spike-mediated "topdown" and "bottom-up" communication, both within and between brain areas. This optimization might have particular importance during motivated anticipation of, and attention to, meaningful events and associations and in response to their anticipated consequences (Von Stein et al., 2000; Fries et al., 2001; Salinas & Sejnowski, 2001; Makeig et al., 2004). This new theory of cortical and scalp-recorded field dynamics requires new data analysis approaches for spatially distributed event-related EEG dynamics.
The standard analysis method to study EEG in an event-related fashion is to focus on event-related potentials (ERPs) by averaging. ERPs are positive or negative voltage deflections seen in the averages of EEG epochs time-locked to a class of repeated stimulus or response events. However, this approach assumes that ERPs are superimposed on ongoing background EEG "noise" with amplitude and phase distributions that are completely unrelated to the task. This view of ERPs has been challenged in the last two decades. First, time-frequency analysis of single-trial EEG signals shows that EEG is 66 SELIN AVIYENTE
not solely random noise; rather, there are event-related changes in the magnitude and phase of EEG oscillations at specific frequencies (Makeig et al., 2004). The early work in this area focused on spectral analysis of EEG signals, which breaks down the oscillatory EEG waveforms into sinusoids at different frequencies, reflecting the role of different frequency bands in cognitive function. Second, ERPs themselves may represent transient phase resetting of ongoing EEG by experimental events, leading to transient timeand phase locking of frequency specific oscillations (Makeig et al., 2004; Makeig et al., 2002). Makeig and colleagues (2002) have introduced the event-related brain dynamics framework, which emphasizes the spectral decomposition of single-trial event-related EEG epochs in order to separately examine event-related changes in the magnitude and phase of oscillations at different frequencies. However, spectral analysis assumes stationarity of the signal, in spite of the fact that information processing in the brain is mostly reflected by fast dynamic changes in EEG. Even though the Fourier transform provides a complete representation of the time series, the resulting power spectrum is only interpretable for stationary signals; non-stationarities are encoded in the phase spectrum, which is typically impossible to interpret visually. Spectral analysis is only capable of reflecting the average or global frequency content, rather than illustrating the local activity. The non-stationarities in the EEG signal are the primary motivation for methods that can capture simultaneously the variation of signal energy across time and frequency.
Time-frequency analyses of EEG provide additional information about neural synchrony not apparent in ongoing EEG activity or in ERPs. They can tell us which frequencies have the most power at different time points and how their phase synchronizes across time and space. Thus, using time-frequency analyses, we can assess changes in power and synchronization of EEG within or between spatial locations across trials with respect to the onset of tasks. However, it is important to note that timefrequency analysis cannot by itself determine the cause of the changes in EEG power, that is, whether the change is due to changes in the magnitude of the oscillations or to changes in their degree of synchronization (Yeung, 2004; Roach & Mathalon, 2008).
The goal of this chapter is to give an overview of different time-frequency analysis tools for both quantifying the changes in EEG power across time and frequency and the changes in phase synchrony across time, frequency, and space. The different methods discussed in this chapter can be divided into three categories: linear, nonlinear, and data-driven or adaptive methods. The first category of methods focus on simple extension of Fourier transform to the non-stationary signal that is, short-time Fourier transform or sliding window approach, and the continuous wavelet transform. The second category of methods focus on Cohen's class of time-frequency distributions (TFDs) that compute the spectrum of the time-varying auto-correlation function of the signal, rather than the signal itself. In this manner, these distributions are highly nonlinear but offer high-resolution visualizations of EEG dynamics. The last category of methods stem from recent advances in signal processing that focus on sparse signal representation. The two methods reviewed under this category are matching pursuit (MP) and empirical mode decomposition (EMD).
TIME-FREQUENCY DECOMPOSITION METHODS 67
## **4.2 Linear Time-Frequency Decomposition Methods**
#### **4.2.1 Short-Time Fourier Transform**
The earliest method that allowed for the time-frequency representation of a signal's energy distribution was the short-time Fourier transform (STFT), also known as the windowed Fourier transform. It relies on an estimation of power spectra, through Fourier transform, for short time windows shifted along the time axis. The basic idea of STFT is to break up the signal into small time segments and Fourier analyze each time segment to determine the frequencies that existed in that segment. The totality of such spectra indicates how the spectrum is varying with time. STFT is a linear time-frequency transform that correlates the signal with a family of waveforms that are well-concentrated in time and frequency, compared to standard spectral analysis, which correlates the signal with eternal sinusoids resulting in good frequency localization at the expense of poor time localization. For a signal *x t*( ), its STFT can be expressed as:1
$$S(t,\omega) = \int x(\tau)g(\tau - t)e^{-j\omega\tau}d\tau, \tag{4.1}$$
where *g* ( ) *τ* is the window function. The localization of information provided by STFT depends on the time-frequency spread of the window *g* .
The choice of the length and shape of the window function are the two critical issues in applying STFT to EEG signals. The first problem is usually addressed by considering the existing trade-off between time and frequency resolution determined by the length of the window function. This trade-off, known formally as the uncertainty principle, states that as the length of the window increases in time, localization in time or time resolution goes down while the localization in frequency (frequency resolution) increases (Cohen, 1995). Similarly, if the window length decreases, time resolution increases at the expense of frequency resolution. In practice, the length of the window is usually selected by trying different window lengths in order to obtain an optimal trade-off. This optimal length is highly dependent on the underlying signal's properties, such as the rate with which it changes. The second issue of selecting the shape of the window has been addressed in a more rigorous way with the resolution of some common windows mathematically formulated (Mallat, 1999). For numerical applications, the window function is usually selected as a symmetric and real function. By choosing an appropriate window function, one can obtain localization around the time point of interest, *t*. For good time-frequency resolution, the ratio of the first sidelobes to the peak of the
1 All integrals are from −∞ to ∞ unless otherwise noted.
68 SELIN AVIYENTE
window function should be large, that is, the rate of decay the window function in the frequency domain, *G*( ) *ω* , should be fast. Some common window functions include the rectangular, Hamming, Hanning, and Gaussian window functions. Rectangular windows have the worst frequency resolution due to the sharp transition of the window function. Gaussian window achieves the best joint time and frequency localization as it meets the lower bound of the uncertainty principle. In STFT, the duration of the time window is fixed in contrast to the wavelet transform, which in turn provides uniform frequency resolution. STFT is a complex valued time-frequency representation, and an energy distribution can be obtained as| , *S t*( ) *ω* | 2 , known as the spectrogram.
#### **4.2.2 Continuous Wavelet Transform**
Continuous wavelet transforms (CWT) describe a class of spectral decomposition methods that are conceptually related to the STFT. Unlike STFT, where the signals are decomposed into localized sinusoids, in the wavelet transform the signals are decomposed in terms of "small waves" of limited duration with an average value of zero. The wavelet transform of a signal *x t*( ) is given by:
$$W(t,s) = \int x(\tau) \frac{1}{\sqrt{s}} \psi^* \left(\frac{\tau - t}{s}\right) d\tau, \tag{4.2}$$
where *ψ* is the wavelet function and *s* is the scale parameter. Similar to STFT defined in Eq. 4.1, the wavelet transform finds the decomposition of a given signal in terms of time-frequency atoms. However, in this case, the time-frequency atoms are the timeshifted and scaled versions of the mother wavelet, *ψ*. For this reason, wavelet transform should be thought of as a time-scale decomposition rather than a TFD, as the signal is not decomposed in terms of sinusoids across different frequencies. One of the major differences between STFT and CWT is the time-frequency localization. In STFT, the frequency localization is uniform due to the fixed window size. On the other hand, for CWT the time resolution is variable, with shorter time windows for higher frequencies and longer time windows for lower frequencies. This variable time resolution closely matches the structural properties of ERP signals and has made CWT an attractive choice for time-frequency analysis of ERPs (Roach & Mathalon, 2008; Demiralp et al., 2001; Polikar et al., 2007). Using CWT, the ERP can be decomposed across several orthogonal functions, wavelets, with overlapping time courses at different scales.
While any number of wavelet functions can be used for ERP analysis, the wavelet must provide a biologically plausible fit to the signal being modeled. Some commonly used wavelets for EEG and ERP analysis are real wavelets, such as splines, and analytic wavelets, such as the Morlet wavelet and the Generalized Morse Wavelet (GMW). In particular, the analytic wavelets are useful to obtain both energy and phase information of the underlying oscillations. The Morlet wavelet is one that has been commonly used TIME-FREQUENCY DECOMPOSITION METHODS 69
for EEG/ERP analysis. The Morlet wavelet is defined as a complex sinusoid tapered by a Gaussian given as:
$$\psi(t) = e^{j2\pi ft} e^{-\frac{t^2}{2\sigma^2}},$$
(4.3)
where $\sigma$ is the width of the Gaussian and is reciprocally related to the frequency in order to retain the wavelet's scaling properties. By this scaling, one obtains the same number of significant wavelet cycles at all frequencies. Thus, the Morlet wavelet transform has a different time and frequency resolution at each scale. Therefore, at high frequencies the temporal resolution of a wavelet is better than at low frequencies. However, the inverse is true for the frequency resolution of the wavelet transform. Convolution with the complex Morlet wavelet results in a complex-valued signal from which instantaneous power and phase can be extracted at each time point. Wavelet convolution can be conceptualized as a template matching or bandpass filtering. Convolutions with Morlet wavelets can be computed for multiple frequencies in order to yield a time-frequency representation. Since Morlet wavelet is a complex function, the corresponding wavelet transform is also complex, where the real part corresponds to the bandpass filtered signal and the imaginary part corresponds to Hilbert transform of the signal. There are several advantages of Morlet wavelets for EEG/ERP analysis (Cohen, 2018). One is that the Morlet wavelet is Gaussian shaped in the frequency domain and the absence of sharp edges minimizes ripple effects. Second, the results of Morlet convolution retain the temporal resolution of the original signal. Third, wavelet convolution is computationally efficient and can be implemented using the fast Fourier transform. The wavelet power spectrum, also known as the scalogram, can be obtained as $\left| W(t,s) \right|^{2}$ .
## **4.3 Nonlinear Time-Frequency Analysis: Cohen's Class of Time-Frequency Distributions**
For a signal, *x* ( )*t* , a bilinear TFD, *C t*( ) ,*ω* , from Cohen's class can be expressed as (Cohen, 1995):
C(t,\omega) = \iiint \phi(\theta,\tau) x \left(u + \frac{\tau}{2}\right) x^\* \left(u - \frac{\tau}{2}\right) e^{j(\theta u - \theta t - \tau \omega)} du \, d\theta \, d\tau,
$$C(t,\omega) = \iiint \phi(\theta,\tau) x \left(u + \frac{\tau}{2}\right) x^* \left(u - \frac{\tau}{2}\right) e^{j(\theta u - \theta t - \tau \omega)} du \, d\theta \, d\tau$$
(4.4)
where *φ θ*( ) , *τ* is the kernel function in the ambiguity domain (*θ*, *τ*). Unlike linear transforms, which first multiply the signal with a time-limited window function before 70 SELIN AVIYENTE
computing its Fourier transform, Cohen's class of distributions compute the Fourier transform of the local autocorrelation function. In this manner, the signal acts like a window on itself. The kernel *φ θ*( ) , *τ* acts like a filter on this local autocorrelation function and determines which parts to preserve. TFDs represent the energy distribution of a signal over time and frequency, simultaneously. Some of the most desired properties of TFDs are the energy preservation, the marginals, and the reduced interference. Some common TFDs used for EEG and ERP analysis include the Wigner distribution and its filtered versions (Tağluk et al., 2005; Abdulla & Wong, 2011).
#### **4.3.1 Wigner Distribution**
The Wigner distribution is defined as:
$$W(t,\omega) = \int x \left(t + \frac{\tau}{2}\right) x^* \left(t - \frac{\tau}{2}\right) e^{-j\omega\tau} d\tau, \tag{4.5}$$
where *x t*( ) is the signal and *τ* is the time lag variable. The Wigner distribution computes the Fourier transform of the local autocorrelation of the signal as the kernel *φ*( ) *θ τ*, = 1. As the kernel acts as an all pass filter, Wigner distribution keeps the whole autocorrelation function before transforming it. This provides a high time-frequency resolution. In fact, it has been shown that the Wigner distribution provides the highest time-frequency resolution among all Cohen's class of TFDs (Cohen, 1995). It overcomes some of the shortcomings of the spectrogram as there is no dependency on the choice of the window. Moreover, the Wigner distribution provides accurate instantaneous frequency estimates and is an accurate energy distribution as it satisfies the marginals.
However, Wigner distribution is a bilinear function of signals. Therefore, Wigner distribution of multi-component signals or mono-component signals with curved timefrequency supports will be cluttered by spurious terms called cross-terms. The existence of cross-terms may decrease the interpretability of the TFD. ERPs, like other nonstationary signals, require an analysis technique that is free from cross-terms.
#### **4.3.2 Reduced Interference Distributions (RIDs)**
In order to reduce cross-terms that appear in the Wigner distribution, the past twenty years demonstrates a move towards using reduced interference distributions (RIDs), designed using kernel functions *φ θ*( ) , *τ* 1 for *θτ* 0 , which concentrate the energy across the auto-terms, and satisfy the energy preservation and the marginals (Jeong & Williams, 1992). The kernel function *φ θ*( ) , *τ* is usually designed in the ambiguity plane as the auto-terms tend to be close to the origin and the cross-terms away from the origin TIME-FREQUENCY DECOMPOSITION METHODS 71
of the ambiguity plane. This allows for interpretation of the kernel function as a lowpass filter that attempts to reject the cross-terms and leave the auto-terms unchanged. The shape of the filter can be adapted to the analysis of the desirable signal components depending on the nature of the signal. For RIDs, *φ*( ) *θ τ*, = *h*( ) *θτ* , where *h* is a monotonously decreasing function to ensure that the parameterization function is a low-pass filter in the ambiguity plane. Depending on the canonical form of *h*, the resultant RIDs have different cross-term rejection capabilities. Some commonly used RIDs include Choi–Williams (CW) (Jeong & Williams, 1992), B-distribution (Zhao et al., 1990), Born–Jordan, and Zhao–Atlas–Marks (Zhao et al., 1990).
Since these distributions will be implemented in discrete-time, discrete-time TFD of size 2 1 *N N* + × 2 1 + can be defined as:
$$TFD(n, \omega; \psi) = \sum_{n_1 = -N}^{N} \sum_{n_2 = -N}^{N} x(n + n_1) x^*(n + n_2) \psi\left(-\frac{n_1 + n_2}{2}, n_1 - n_2\right) e^{-j\omega(n_1 - n_2)}, \quad (4.6)$$
where*ψ* is the discrete-time kernel in the time and time-lag domain. The most commonly used discrete-time kernel for EEG/ERP analysis is the binomial kernel, which is given by
$$\psi(n,m) = 2^{-|m|} \begin{pmatrix} |m| \\ n + \frac{|m|}{2} \end{pmatrix} \text{ for } |n| \le \frac{|m|}{2}.$$
## **4.4 Data-Driven or Adaptive Time-Frequency Representations**
Unlike the first two types of time-frequency transforms, the methods reviewed in this section do not directly result in time-frequency energy distributions, but rather result in a description of the ERP dynamics as a sum of a few numbers of distinct components. These components may be either data-driven, that is, derived directly from the signals, or selected from a large dictionary of atoms. Usually, these components are localized in time and frequency and thus can be thought of as a decomposition of the eventrelated EEG signals into a few distinct time-frequency elements. Thus, the resulting components can be visualized using any transform discussed in the previous sections to obtain a time-frequency spectrum. For this reason, these are sometimes considered as time-frequency analysis tools in the literature. By the nature of the algorithms used to derive these components, these methods are nonlinear. The first one of these methods, EMD, is data-driven and the resulting components usually represent the different frequency bands of EEG. The second method, MP, can be thought of as an extension of wavelet transform. However, unlike the wavelet functions, which usually form an 72 SELIN AVIYENTE
orthonormal basis for the signal space, the time-frequency atoms used in MP form an overcomplete dictionary. This means that the set of functions used to express the signal is more than necessary. This overcompleteness results in sparse representation of the EEG/ERP signals. These atoms are pre-determined similar to the wavelet transform and can be selected by the user based on the characteristics of the signals. Some example atoms could be a combination of sinusoids and wavelets, Gabor functions, etc. This efficiency in representation of the signals with a few time-frequency atoms comes at the expense of computational complexity. Unlike wavelet transform, which is computationally efficient, MP usually relies on greedy algorithms (Mallat & Zhang, 1993; Tropp & Gilbert, 2007).
#### **4.4.1 Empirical Mode Decomposition**
EMD is a fully adaptive, data-driven approach that decomposes a signal into oscillations inherent to the data, referred to as intrinsic mode functions (IMFs) (Huang et al., 1998). Finding the IMFs is equivalent to finding the band-limited oscillations underlying the observed signal. Extracting the IMFs is similar to finding the harmonic components in Fourier analysis. However, the IMF is much more general than the harmonic component since it can be modulated both in amplitude and frequency, while a harmonic component has constant amplitude and frequency. The amplitude and frequency modulations are possible because the decomposition depends on the local characteristic time scale of the data. Because the decomposition depends on the local characteristic time scale, EMD is suitable for application to non-stationary signals such as ERPs. The EMD algorithm decomposes the signal *x t*( ) as *x t C t r t i i M* ( ) = ( ) + ( ) ∑ =1 where *C t i* ( ) , *i M* = …1, , are the IMFs and *r t*( ) is the residue. The algorithm can be described as follows:
- 1. Let *x t* ( ) = *x t*( ) .
- 2. Identify all local maxima and minima of *x*( )*t* .
- 3. Find two envelopes *e t min* ( ) and *e t max* ( ) that interpolate through the local minima and maxima, respectively.
- 4. Let *d t x t e t e t* ( ) *min max* = ( ) − ( ) ( ) + ( ) 1 2 as the detail part of the signal.
- 5. Let *x t* ( ) = *d t*( ) and go to step 2 and repeat until *d t*( ) becomes an IMF. The two IMF criteria are: a) the number of extrema and the number of zero-crossings must either be equal or differ at most by one; b) At any point, the mean value of the envelope defined by the local maxima and the envelope defined by the local minima is zero.
- 6. Compute the residue *r t*( ) = *x t*( ) − *d t*( ) and go back to step 1 until the energy of the residue is below a threshold.
TIME-FREQUENCY DECOMPOSITION METHODS 73
Although EMD has the ability to extract ERP components, it suffers from the mode mixing problem (Huang et al., 2003). That is, the different time-frequency components may not directly correspond to the different IMFs, which makes it difficult to determine the distinct ERP components. To overcome the problem of mode mixing, Wu and Huang (2009) recommend ensemble EMD (EEMD), a noise-assisted data-analysis method. The output of EEMD is a set of IMFs generated from ensemble means of trials by repeating EMD on the same signal with different sets of Gaussian noise. A further potential drawback of EMD has been put forth by Flandrin and colleagues (2004), who showed that EMD behaves as a dyadic filter bank. This poses the concern that EMD may naturally lead to such a decomposition in all data, which implies that important oscillations may not be identified if they do not adhere to a dyadic frequency relationship with one another.
Once the IMFs are obtained, Hilbert spectral analysis, also known as Hilbert–Huang Transform (HHT), can be used to evaluate the frequency content of each IMF. Hilbert spectral analysis provides the instantaneous frequency of each IMF. According to Huang and colleagues (2011), the instantaneous frequency could represent the nonlinear and non-stationary signals without resorting to the mathematical artifact of harmonics. Like measuring ERPs, averaging IMFs across trials provides event-related modes (ERMs). Based on the instantaneous frequency of ERMs, ERP components can be extracted by summing ERMs (Cong et al., 2009; Williams et al., 2011; Wu et al., 2012) or using an ERM within a frequency range.
#### **4.4.2 Matching Pursuit**
The MP algorithm, originally proposed by Mallat and Zhang (1993), relies on an adaptive approximation of a signal by means of waveforms chosen from a very large and redundant dictionary of functions. MP provides high-resolution signal analysis with good resolution in time-frequency space and allows for parametric description of both periodic and transient signal features. It is suitable for analysis of non-stationary signals and for the investigation of dynamic changes of brain activity. MP aims at obtaining a sparse linear representation of a signal, *x t*( ), in terms of functions, *gi* (sometimes referred to as atoms), from an overcomplete dictionary, *D*, using an iterative search algorithm (Mallat & Zhang, 1993):
$$x(t) = \sum_{i=1}^{M} a_i g_i(t). \tag{4.7}$$
The problem of choosing *M* functions, which explain the largest proportion of energy of a given signal, is a computationally complex problem and is known to belong to the class of non-deterministic polynomial-time hard (NP-hard) problems. MP offers a tractable suboptimal solution, obtained by an iterative algorithm.
74 SELIN AVIYENTE
In the first step of the iterative procedure, we choose the element of the dictionary that gives the largest inner product with the signal, that is, *g x g g D i i* 1 = ∈ argmax , . This first element of the dictionary is subtracted from the signal to obtain the residue. The iterative procedure is repeated on the subsequent residual, *R x k* . This procedure can be summarized as:
- 1. Define the 0th order residual as *R x x* 0 = .
- 2. For the *k* th order residual, *R x k* , select the best atom such that the inner product between the residual and the atom is maximized
$$g_k = \operatorname{argmax}_{g_i \in D} \left| \left\langle R^k x, g_i \right\rangle \right|.$$
(4.8)
3. Compute the residue *R x k*+1 as
$$R^{k+1}x = R^k x - \left\langle R^k x, g_k \right\rangle g_k. \tag{4.9}$$
4. After *M* iterations, the following linear representation is obtained:
$$x =
\sum_{k=1}^{M} \left\langle R^{k} x, g_{k} \right\rangle g_{k} + R^{M+1} x. \tag{4.10}$$
The procedure converges to $x$ in the limit, that is, $x = \sum_{k=1}^{\infty} \langle R^k x, g_k \rangle g_k$ and preserves signal energy. From this representation, one can derive a TFD of a signal's energy by adding Wigner distributions of selected atoms.
The overcomplete dictionary, *D* , can be designed to fit the class of signals at hand. Two important requirements for a dictionary are its descriptive power, that is, its ability to represent the signals of interest with relatively few atoms (sparsity), and its interpretability, that is, that the parameters indexing the atoms convey information. Although overcomplete dictionaries do not provide uniqueness of decomposition, they have more descriptive power than more classical, orthogonal dictionaries, such as wavelets. Regarding interpretability, the choice of atoms and their parameters is motivated by the types of activities that will be encountered. The dictionary is furthermore supposed to depend continuously on the parameter space (even though for numerical reasons, this space will obviously be discretized). This constraint is imposed only for ease of presentation, but the approach could be generalized, at the cost of some added complexity. For analyzing EEG and ERP signals, previous work has shown that Gabor logons represent the signals with few coefficients (Durka & Blinowska, 2001; Brown et al., 1994; Aviyente, 2007) . Gabor logons also have the advantage of being the most concentrated signals on the time-frequency plane, TIME-FREQUENCY DECOMPOSITION METHODS 75
achieving the lower bound of the time-bandwidth product. A dyadic Gabor dictionary also allows for computationally effective implementation and has been used widely in EEG analysis.
#### **4.4.3 Multichannel Matching Pursuit**
The principle of MP can easily be generalized to the simultaneous decomposition of multiple signals, **X** = $(x^1, x^2, ..., x^r)$ of *r* signals into atoms from the same overcomplete dictionary, *D*. This approach is sometimes referred to as the multichannel MP (MMP) or simultaneous MP in the literature, since it is usually applied to multiple signals collected over multiple channels/sensors or trials ([Gribonval et al., 2008](#page-9-1); [Lelic et al., 2011](#page-9-1); [Sieluzycki et al., 2008](#page-9-1)). Unlike the original MP, MMP represents every component $x^l$ of **X** as a weighted sum of the same elements from the overcomplete dictionary and thus tries to achieve joint sparsity of a collection of signals for a given dictionary. The algorithm can be described as follows:
- 1. Define for each signal *l* the 0th order residual as *R x x* 0 *l l* = .
- 2. For the *k*th order residual, *R x k l*, select the best atom such that the total inner product between the atom and the residuals in each signal is maximized
$$\operatorname{argmax}_{g_i \in D} \sum_{l=1}^{r} \left| \left\langle R^k x^l, g_i \right\rangle \right|. \tag{4.11}$$
3. Compute the residue *R x k l* +1 for all signals:
$$R^{k+1}x^{l} = R^{k}x^{l} - \left\langle R^{k}x^{l}, g_{k} \right\rangle g_{k}. \tag{4.12}$$
4. After *M* iterations, the following linear representation is obtained for each signal:
$$x^{l} =
\sum_{k=1}^{M} \left\langle R^{k} x^{l}, g_{k} \right\rangle g_{k} + R^{M+1} x^{l}.$$
(4.13)
Different implementations of MMP have been employed for ERP analysis, that is, evoked activity MP (EMP) and induced activity MP (IMP) (Bénar et al., 2009). In EMP, the atoms are determined to maximize the correlation with the average signal, and the amplitude is adapted to the individual trials. In this manner, the method accounts for amplitude variability across trials, but not for variability in the parameter space. IMP, on the other hand, maximizes the average energy across trials. Durka and colleagues 76 SELIN AVIYENTE
(2005) have also proposed an alternative approach for simultaneous time-frequency parametrization of multiple EEG recordings by applying the standard MP algorithm to the average of multichannel EEGs. This approach reduces the computational complexity by a factor of*r* at the expense of favoring data with equal phases in all of the channels.
## **4.5 Illustration of Different Time-Frequency Methods for ERP Analysis**
This section illustrates the performance of some of the time-frequency analysis methods discussed earlier for an example ERP signal. In particular, we focus on the error-related negativity (ERN), a neurophysiological marker of performance monitoring. ERN is a negative deflection in the ERP that peaks within 100 ms of an erroneous response at frontocentral recording sites (Moser, 2017; Moran et al., 2015). The ERN is generally considered to be an index of cognitive control-related performance monitoring that is involved in coordinating optimal responding following mistakes. For the purpose of this illustration, we consider ERP obtained by averaging across trials recorded at the FCz electrode for one subject.
First, we compare the performance of linear and nonlinear time-frequency energy distributions, namely the continuous wavelet transform with the Morlet wavelet, and RID with the binomial kernel. From Figure 4.1, a typical ERN waveform with a negative potential occurring in the first 100 ms can be seen, along with different TFDs. From both
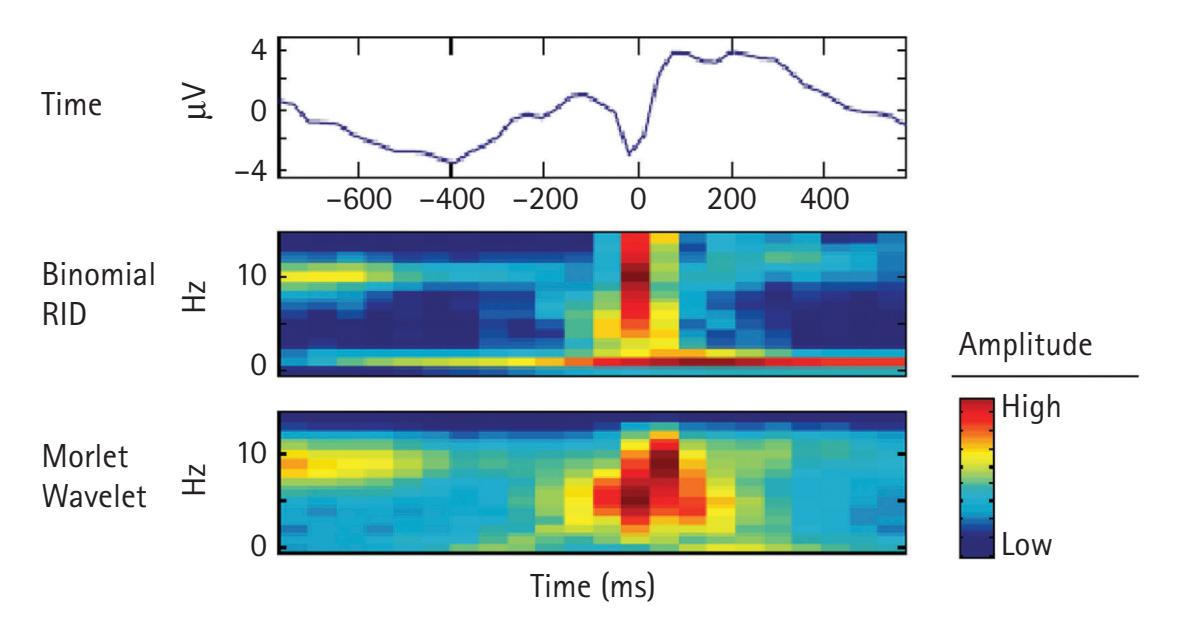
**Figure 4.1** Time-frequency Analysis of ERN waveform. From top to bottom: ERN signal in the time domain, reduced interference distribution (binomial kernel), continuous wavelet transform with Morlet wavelet.
TIME-FREQUENCY DECOMPOSITION METHODS 77
distributions, it is clear that there is high energy corresponding to ERN and P3e, P300 following the error response. The biggest difference between the different distributions is the time and frequency resolution of this component in the time-frequency plane. For RID, there are two distinct time-frequency components; one during ERN localized in the theta band (4–8Hz) and another distributed in time up till 400 ms in the delta (0–2 Hz) band. Morlet wavelet produces a distribution that captures the theta band activity without highlighting the delta band energy. It can be seen from these results that RID has the better time and frequency resolution, whereas the wavelet transform has poorer time and frequency localization. From this comparison, it can be concluded that RID provides better delineation of different ERP components. The results of the CWT may be improved by changing the wavelet type and wavelet scales. Unlike RID, which does not depend on the selection of any parameters, CWT is highly dependent on the user provided parameter values.
Next, we compare the performance of data-driven component extraction methods, EMD and MP. Figure 4.2 illustrates the first four IMFs, along with their Hilbert spectra. This figure shows that the first two IMFs correspond to the ERN time interval, whereas the third and fourth IMFs correspond to the P3e potential. The corresponding timefrequency energy distribution has a high energy concentration in the 100–200 ms and 300–400 ms time intervals within the delta frequency band. These components correspond to the P3e. However, the ERN component is not easily detected from this distribution as it has less energy than P3e.
In a similar manner, Figure 4.3 illustrates an MP spectrum obtained using a Gabor dictionary. The dictionary is constructed using Gabor functions, that is, Gaussian window functions shifted in time and modulated in frequency. The figure illustrates the time-frequency localization of the selected atoms. The figure also shows a high energy atom in the 100–200 ms time interval in the delta band. There are also Gabor functions with negative weights in the 0–100 ms time window around 10–12 Hz frequency band. This corresponds to ERN time window and alpha frequency band.
From these comparisons, it can be seen that RID is the best in terms of separating different ERP oscillations from each other with high resolution. The componentbased methods work better in separating different oscillatory components, such as the IMFs extracted from EMD. However, EMD is not a true time-frequency energy distribution method, as it does not produce an actual spectrum like RID. The current method of visualizing IMFs in the time-frequency plane relies on the Hilbert transform of extracting the individual envelope and instantaneous frequency for each IMF. As the Hilbert transform is not a true time-frequency localization method, the IMFs can also be transformed to the time-frequency plane using different distributions to obtain higher-resolution visualizations. MP, on the other hand, is highly dependent on the selected dictionary atoms. The more suitable the dictionary is for the underlying signal, the sparser the resulting representation. In this particular example, MP wrongly detects alpha components for the ERN time window while missing the theta activity for the same time window. As EMD is data-driven and independent of priors, it performs better than MP for ERP analysis.
78 SELIN AVIYENTE

**Figure 4.2** Empirical mode decomposition for ERP signal: (A) The first four intrinsic mode functions (IMFs) extracted from the ERP signal. (B) The time-frequency spectrum corresponding to the extracted IMFs.
TIME-FREQUENCY DECOMPOSITION METHODS 79
**Figure 4.3** Time-frequency analysis using matching pursuit with a Gabor dictionary.
## **4.6 Time-Frequency-Based Phase Synchrony Analysis**
Although time-frequency energy distribution is effective for studying the spectral content of EEG and ERP oscillations, most of the current approaches focus only on the magnitude spectrum of the oscillations and ignore the phase information. Recent research shows that ERPs result from event-related partial phase resetting of ongoing oscillatory activity along with transient increases in the magnitude of oscillations that are time-locked to the experimental events (Roach & Mathalon, 2008; Makeig et al., 2004). Therefore, it is important to characterize the change in phase information across time and frequency.
Phase synchrony quantifies the relation between the temporal structures of the signals, regardless of signal amplitude (Rosenblum et al., 2000; 2001). Two signals are said to be synchronous if their rhythms coincide. The amount of synchrony between two signals is usually quantified by first estimating the instantaneous phase of the individual signals around the frequency of interest. Traditionally, the instantaneous phase of a given signal is estimated first, and then the phase synchrony is quantified using statistical measures. Conventionally, the instantaneous phase is estimated using the Hilbert transform. However, the Hilbert transform does not 80 SELIN AVIYENTE
provide any selectivity in frequency, the whole range of frequencies is considered to define the instantaneous phase. Therefore, if the signal is broadband, such as in the case of EEG signals, it is necessary to pre-filter it in the frequency band of interest before applying the Hilbert transform, in order to get a proper phase estimate. However, this method relies heavily on the proper selection of the bandpass filter and may suffer from estimation bias. In order to address the shortcomings of the Hilbert transform, different time-frequency transforms have been used to estimate instantaneous phase.
#### **4.6.1 Wavelet-Based Phase Estimation**
One common time-frequency based phase estimation approach employs CWT (Lachaux et al., 1999), in which the phase of the signals is extracted from the coefficients of their continuous wavelet transform using a complex wavelet function, such as the Morlet wavelet at the target frequency. These coefficients are the result of a convolution of the original signal with a time-shifted and frequency-modulated Gaussian function as:
$$W_{x}(t,f) = \int_{-\infty}^{\infty} x(u) \psi_{t,f}^{*}(u) du$$
(4.14)
where $\psi^*_{t,f}(u)$ represents the complex conjugate of the wavelet function. Using the Morlet wavelet $\Psi_{t,f}(u) = \sqrt{f} e^{j2\pi f(u-t)} e^{-\frac{(u-t)^2}{2\sigma^2}}$ , the phase spectrum of $x(t)$ can be evaluated as follows:
$$\Phi_{x}(t,f) = \arg\left[\frac{W_{x}(t,f)}{\left|W_{x}(t,f)\right|}\right]. \tag{4.15}$$
This method of computing time-frequency phase estimation has been shown to yield similar results with respect to the Hilbert transform with the main difference being the increased frequency resolution offered by CWT (Le Van Quyen et al., 2001). The main shortcoming of the CWT-based method is the non-uniform resolution across time and frequency, which results in biased phase estimates (Aviyente et al., 2011).
#### **4.6.2 EMD-Based Phase Estimation**
More recently, EMD- and RID-based phase synchrony estimates have been proposed. While HHT provides a time-frequency energy distribution, EMDs have also been used TIME-FREQUENCY DECOMPOSITION METHODS 81
for quantifying phase synchrony between signal pairs. A problem with current synchrony detection methods such as the Hilbert transform is that they depend on *a priori* selection of bandpass filters. In response to this problem, EMD-based phase synchrony measures have been defined (Rutkowski et al., 2008; Looney et al., 2009; Sweeney-Reed & Nasuto, 2007; Mutlu & Aviyente, 2011). In most of these approaches, the IMFs for each time series were extracted individually and were compared individually against the IMFs from the other time series for computing phase synchrony. This approach has multiple shortcomings. First, the IMFs from the different time series do not necessarily correspond to the same frequency, thus making it hard to compute exact withinfrequency phase synchronization across different EEG channels. Second, the different time series may end up having different numbers of IMFs, which makes it difficult to match the different IMFs for synchrony computation. Finally, Looney and colleages (2009) showed that univariate EMD is not robust under noise and may suffer from mode mixing, which refers to the phenomenon of different modes (or frequencies) existing in a single IMF due to noise or intermittent signal activity.
Recently, extensions of EMD to the multivariate case have been developed including Complex EMD (Tanaka & Mandic, 2007), Rotation Invariant EMD (RIEMD) (Altaf et al., 2007), and Bivariate EMD (BEMD) (Rilling et al., 2007). These complex extensions of EMD decompose data from different sources simultaneously. Looney and colleages (2009) showed that the IMFs obtained in this fashion are matched, not only in number, but also in frequency overcoming problems of uniqueness and mode mixing, and first suggested the idea of using bivariate EMD to compute phase synchrony between two signals and the BEMD was shown to perform better than univariate EMD for quantifying bivariate synchrony. However, this approach still has some shortcomings, as the frequency bands corresponding to IMFs from different bivariate pairs are not necessarily the same. As such, this method is mostly limited to bivariate synchrony analysis and is not as easily generalizable to the whole brain synchrony analysis. Moreover, the multivariate extensions of EMD have been shown to be computationally expensive for computing functional connectivity across the whole brain (Mutlu & Aviyente, 2011).
#### **4.6.3 RID-Based Phase Estimation**
In recent work, we have shown the effectiveness of RID-based phase synchrony estimates compared to Hilbert- and CWT-based estimates (Aviyente & Mutlu, 2011; Aviyente et al., 2011; Sponheim et al., 2011; Aviyente et al., 2017). As most members of Cohen's class of TFDs are real-valued, they do not preserve the phase information. For this reason, we introduce a complex TFD, the Rihaczek distribution, to extract time- and frequency-dependent phase estimates. Rihaczek introduced the complex energy distribution and gave a plausibility argument based on physical grounds (Rihaczek, 1968).
For a signal, $x(t)$ , Rihaczek distribution is expressed as
$$C(t, \omega) = \frac{1}{\sqrt{2\pi}} x(t) X^{*}(\omega) e^{-j\omega t}$$
82 SELIN AVIYENTE
where $X^{\ast}(\omega)$ is the complex conjugate of the Fourier transform of the signal and $C(t, \omega)$ measures the complex energy of a signal around time, $t$ and frequency, $\omega$ . The complex energy density function provides a fuller appreciation of the properties of phase-modulated signals that is not available with other TFDs. Rihaczek distribution is a bilinear, time- and frequency-shift covariant, complex-valued TFD belonging to Cohen's class. This distribution satisfies the marginals and preserves the energy of the signal. Rihaczek distribution provides both a time-varying energy spectrum as well as a phase spectrum, and thus is useful for estimating the phase synchrony between any two signals. One of the disadvantages of Rihaczek distribution, similar to other quadratic TFDs, is the existence of cross-terms for multicomponent signals. In order to get rid of these cross-terms, in previous work (Aviyente et al., 2011), we proposed to apply a kernel function such as the CW kernel to filter the cross-terms. The resulting distribution can be written as:C(t,\omega) = \iint \exp\left(-\frac{(\theta\tau)^2}{\sigma}\right) \exp\left(j\frac{\theta\tau}{2}\right) A(\theta,\tau) e^{-j(\theta t + \tau\omega)} d\tau d\theta,
$$C(t,\omega) = \iint \exp\left(-\frac{(\theta\tau)^2}{\sigma}\right) \exp\left(j\frac{\theta\tau}{2}\right) A(\theta,\tau) e^{-j(\theta t + \tau\omega)} d\tau d\theta$$
(4.16)
where *e j* 2 is the kernel function for the Rihaczek distribution. This new distribution, which will be referred to as RID–Rihaczek, will have an equivalent time-frequency kernel *φ θ τ θτ θτ* , ( ) ( ) = − *e e j* 2 2 . Since this kernel satisfies the constraints, *φ*( ) *θ φ* , , 0 0 = ( ) *θ φ* = ( ) 0 0, = 1, the corresponding distribution will both satisfy the marginals and preserve the energy, as well as be a complex energy distribution at the same time. The value of *σ* can be adjusted to achieve a desired trade-off between resolution and the number of crossterms retained. The phase estimates from RID-Rihaczek distribution can be obtained as
$$\phi(t,\omega) = \arg\left[\frac{C(t,\omega)}{|C(t,\omega)|}\right]$$
. This phase estimate has been shown to be more robust to noise
and has uniformly high resolution in time and frequency compared to wavelet-based phase estimates (Aviyente & Mutlu, 2011).
#### **4.6.4 Different Measures of Phase Synchrony**
Once the phase difference between two signals is estimated through a time-frequencybased method, it is important to quantify the amount of synchrony. The most common scenario for the assessment of phase synchrony entails the analysis of the synchronization between pairs of signals. In the case of noisy oscillations, the length of stable segments of the relative phase gets very short; further, the phase jumps occur in both directions, so the time series of the relative phase *φx y t* , ( )looks like a biased random walk (unbiased only at the center of the synchronization region). Therefore, the direct analysis of the unwrapped phase differences *φx y t* , ( ) has been used seldomly. As a result, phase synchrony can only be detected in a statistical sense. Two different indices TIME-FREQUENCY DECOMPOSITION METHODS 83
have been proposed to quantify the synchrony based on the relative phase difference, that is, *φx y t* , ( ) is wrapped into the interval [0 2, *π*) . The first index uses an informationtheoretic criterion to quantify synchronization. This measure studies the distribution of *φx y t* , ( ) by partitioning the interval [0 2, *π*) into *L* bins and comparing it with the distribution of the cyclic relative phase obtained from two series of independent phases. This comparison is carried out by estimating the Shannon entropy of both distributions, that is, that of the original phases, and that of the independent phases, and computing the normalized difference (Quiroga et al., 2002). The second metric, phase synchronization index, is also known as the mean phase coherence and computed as < ( ) ( ) > + < ( ) ( ) > = − ( ) *cos t sin t N* ∑*e xy xy N j t xy k* Φ Φ 2 2 Φ 1 1 . It is a measure of how the rela-
tive phase is distributed over the unit circle. If the two signals are phase synchronized, the relative phase will occupy a small portion of the circle and mean phase coherence is high. This measure is equal to 1 for the case of complete phase synchronization and tends to zero for independent oscillators.
=
0
*k*
These different measures of synchrony can be used to quantify three different types of synchronization from EEG/ERP signals, depending on the application. The major difference between the different implementations of phase synchrony is whether the consistency of phase differences is measured across time, trials, or channels. Phase Locking Value (PLV) quantifies the consistency of the phase differences across trials between two channels as follows: *PLV t N j t k N x y k* , , ( ) *ω φ* = ( ) , ( ) *ω* = ∑1 1 exp , where *k* is the trial number and *N* is the number of trials. This measure is also known as the interchannel phase synchrony (ICPS). It is commonly used to estimate phase-locking in experimental situations, common in neurocognitive studies, where a subject is presented with a sequence of similar stimuli. Single trial phase-locking value (S-PLV), on the other hand, allows us to measure the significance of synchronies in single trials, and does not depend on block repetition of events. The variability of phase-difference is not measured across trials, but across successive time-steps, around a target latency. Specifically, a smoothed or S-PLV is defined for each individual trial. Finally, inter-trial phase synchrony (ITPS) quantifies the consistency of phase values for a given frequency band at each point in time over trials, in one particular electrode. ITPC is defined as
The following equation illustrates the ITPC:
$$ITPC(t,\omega) = \left| \frac{1}{N} \sum_{k=1}^{N} \exp(j\phi_k(t,\omega)) \right|$$
where *N* is the number of trials and \(\phi\_k(t,\omega)\) is the
phase of the *k*th trial for each time and each frequency point. ITPC thus reflects the extent to which oscillation phase values are consistent over trials at that point in timefrequency plane. Note that this measure of phase coherence does not differentiate between possible biophysical mechanisms underlying phase consistency, such as phase reset or phase "smearing". Rather, this measure simply indicates the statistical probability of increased phase consistency between trial and baseline epochs.
84 SELIN AVIYENTE
### **4.7 Summary**
This chapter reviewed some of the basic time-frequency methods for analyzing ERP dynamics. We first introduced the different transforms that have been used to analyze the transient ERP activity. These transforms can be divided into three categories: linear methods such as STFT and CWT, data-adaptive methods such as EMD, and nonlinear methods such as Cohen's class of distributions. Although the overall goal of all of these methods is to determine the dynamics of transient activity, the mathematical principles upon which they rely are quite different. These differences in mathematical formulation lead to different computational complexities. Therefore, it is important to understand how the different methods can be used for different applications and purposes. For example, if the goal is to visualize the energy distribution of the transient ERP activity in time and frequency simultaneously, then Cohen's class of distributions (such as the RID) performs the best. Even though this method is the most complex in terms of computational complexity, it offers very high time-frequency resolution, which in turn provides a way to delineate different ERP components from each other. However, if the goal is to obtain a compact representation of the ERP signals in terms of a few physiologically meaningful components, then data-adaptive methods like EMD and MP are more suitable and computationally efficient. This chapter also shows how the same mathematical transforms can be used to study ERP dynamics through both energy distributions and phase synchrony in the time-frequency domain. While the energy distributions focus on the univariate activity, that is, dynamics within a certain brain region or electrode, the phase synchrony quantifies the dynamics across brain regions. In this manner, it is possible to obtain a better understanding of ERP timing, synchronization across time, frequency, and space.
### **REFERENCES**
- Abdulla, W. & Wong, L. (2011). Neonatal EEG signal characteristics using time frequency analysis. *Physica A: Statistical Mechanics and its Applications*, *390*(6), 1096–1110.
- Altaf, M. U. B., Gautama, T., Tanaka, T., & Mandic, D. P. (2007). Rotation invariant complex empirical mode decomposition. In *2007 IEEE international conference on acoustics, speech and signal processing*-ICASSP'07, vol. 3 (pp. III–1009). IEEE.
- Aviyente, S. (2007). Compressed sensing framework for EEG compression. In *Proceedings of* IEEE/SP: 14th *workshop on statistical signal processing* (pp. 181–184). IEEE. Doi: 10.1109/ SSP.2007.4301243.
- Aviyente, S., Bernat, E. M., Evans, W. S., & Sponheim, S. R. (2011). A phase synchrony measure for quantifying dynamic functional integration in the brain. *Human Brain Mapping*, *32*(1), 80–93.
- Aviyente, S. & Mutlu, A. Y. (2011). A time-frequency-based approach to phase and phase synchrony estimation. *IEEE Transactions on Signal Processing*, *59*(7), 3086–3098.
TIME-FREQUENCY DECOMPOSITION METHODS 85
- Aviyente, S., Tootell, A., & Bernat, E. M. (2017). Time-frequency phase-synchrony approaches with ERPs. *International Journal of Psychophysiology*, *111*, 88–97.
- Bénar, C. G., Papadopoulo, T., Torrésani, B., & Clerc, M. (2009). Consensus matching pursuit for multi-trial EEG signals. *Journal of Neuroscience Methods*, *180*(1), 161–170.
- Brown, M. L., Williams, W. J., & Hero, A. O. (1994). Non-orthogonal Gabor representation of biological signals. In Proceedings of ICASSP '94: IEEE *international conference on acoustics, speech and signal proces*sing, vol. 4 (pp. IV/305-IV/308). IEEE. doi: 10.1109/ ICASSP.1994.389742.
- Cohen, L. (1995). *Time-frequency analysis*, vol. 778. Prentice Hall.
- Cohen, M. X. (2018). A better way to define and describe Morlet wavelets for time-frequency analysis. *bioRxiv* [online], 397182.
- Cong, F., Sipola, T., Huttunen-Scott, T., Xu, X., Ristaniemi, T., & Lyytinen, H. (2009). Hilbert-Huang versus Morlet wavelet transformation on mismatch negativity of children in uninterrupted sound paradigm. *Nonlinear Biomedical Physics*, *3*(1), 1.
- Demiralp, T., Ademoglu, A., Istefanopulos, Y., Başar-Eroglu, C., & Başar, E. (2001). Wavelet analysis of oddball p300. *International Journal of Psychophysiology*, *39*(2–3), 221–227.
- Durka, P. J. & Blinowska, K. J. (2001). A unified time-frequency parametrization of EEGs. *IEEE Engineering in Medicine and Biology*, *20*(5), 47–53.
- Durka, P. J., Matysiak, A., Montes, E. M., Valdés Sosa, P., & Blinowska, K. J. (2005). Multichannel matching pursuit and EEG inverse solutions. *Journal of Neuroscience Methods*, *148*(1), 49–59.
- Flandrin, P., Rilling, G., & Goncalves, P. (2004). Empirical mode decomposition as a filter bank. *IEEE Signal Processing Letters*, *11*(2), 112–114.
- Fries, P., Reynolds, J. H., Rorie, A. E., & Desimone, R. (2001). Modulation of oscillatory neuronal synchronization by selective visual attention. *Science*, *291*(5508), 1560–1563.
- Gribonval, R., Rauhut, H., Schnass, K., & Vandergheynst, P. (2008). Atoms of all channels, unite! Average case analysis of multi-channel sparse recovery using greedy algorithms. *Journal of Fourier Analysis and Applications*, *14*(5–6), 655–687.
- Hassanpour, H., Mesbah, M., & Boashash, B. (2004). Time-frequency feature extraction of newborn EEG seizure using SVD-based techniques. *EURASIP Journal on Applied Signal Processing*, *2004*, 2544–2554.
- Huang, N. E., Shen, Z., Long, S. R., Wu, M. C., Shih, H. H., Zheng, Q., et al. (1998). The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. *Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences*, *454*(1971), 903–995.
- Huang, N. E., Wu, M-L., Qu, W., Long, S. R., & Shen, S. S. P. (2003). Applications of Hilbert– Huang transform to non-stationary financial time series analysis. *Applied Stochastic Models in Business and Industry*, *19*(3), 245–268.
- Huang, Y. X., Schmitt, F. G., Hermand, J-P., Gagne, Y., Lu, Z. M., Liu, Y. L., et al. (2011). Arbitrary-order Hilbert spectral analysis for time series possessing scaling statistics: Comparison study with detrended fluctuation analysis and wavelet leaders. *Physical Review E*, *84*(1), 016208.
- Jeong, J. & Williams, W. J. (1992). Kernel design for reduced interference distributions. *IEEE Transactions on Signal Processing*, *40*(2), 402–412.
- Lachaux, J-P., Rodriguez, E., Martinerie, J., & Varela, F. J. (1999). Measuring phase synchrony in brain signals. *Human Brain Mapping*, *8*(4), 194–208.
86 SELIN AVIYENTE
- Lelic, D., Gratkowski, M., Hennings, K., & Drewes, A. M. (2011). Multichannel matching pursuit validation and clustering—a simulation and empirical study. *Journal of Neuroscience Methods*, *196*(1), 190–200.
- Le Van Quyen, M., Foucher, J., Lachaux, J-P., Rodriguez, E., Lutz, A., Martinerie, J., & Varela, F. J. (2001). Comparison of Hilbert transform and wavelet methods for the analysis of neuronal synchrony. *Journal of Neuroscience Methods*, *111*(2), 83–98.
- Looney, D., Park, C., Kidmose, P., Ungstrup, M., & Mandic, D. P. (2009). Measuring phase synchrony using complex extensions of EMD. In *2009 IEEE/SP 15th workshop on statistical signal processing* (pp. 49–52). IEEE.
- Makeig, S., Debener, S., Onton, J., & Delorme, A. (2004). Mining event-related brain dynamics. *Trends in Cognitive Sciences*, *8*(5), 204–210,
- Makeig, S., Westerfield, M., Jung, T-P., Enghoff, S., Townsend, J., Courchesne, E., & Sejnowski, T. J. (2002). Dynamic brain sources of visual evoked responses. *Science*, *295*(5555), 690–694. Mallat, S. (1999). *A wavelet tour of signal processing*. Elsevier.
- Mallat, S. G. & Zhang, Z. (1993). Matching pursuits with time-frequency dictionaries. *IEEE Transactions on Signal Processing*, *41*(12), 3397–3415.
- Moran, T. P., Bernat, E. M., Aviyente, S., Schroder, H. S., & Moser, J. S. (2015). Sending mixed signals: Worry is associated with enhanced initial error processing but reduced call for subsequent cognitive control. *Social Cognitive and Affective Neuroscience*, *10*(11), 1548–1556.
- Moser, J. S. (2017). The nature of the relationship between anxiety and the error-related negativity across development. *Current Behavioral Neuroscience Reports*, *4*(4), 309–321.
- Mutlu, A. Y. & Aviyente, S. (2011). Multivariate empirical mode decomposition for quantifying multivariate phase synchronization. *EURASIP Journal on Advances in Signal Processing*, *2011*(1), 615717.
- Nunez, P. L. & Srinivasan, R. (2006). *Electric fields of the brain: The neurophysics of EEG*. Oxford University Press.
- Polikar, R., Topalis, A., Green, D., Kounios, J., & Clark, C. M. (2007). Comparative multiresolution wavelet analysis of ERP spectral bands using an ensemble of classifiers approach for early diagnosis of Alzheimer's disease. *Computers in Biology and Medicine*, *37*(4), 542–558.
- Quiroga, R. Q., Kraskov, A., Kreuz, T., & Grassberger, P. (2002). Performance of different synchronization measures in real data: a case study on electroencephalographic signals. *Physical Review E*, *65*(4), 041903.
- Rihaczek, A. (1968). Signal energy distribution in time and frequency. *IEEE Transactions on Information Theory*, *14*(3), 369–374.
- Rilling, G., Flandrin, P., Gonçalves, P., & Lilly, J. M. (2007). Bivariate empirical mode decomposition. *IEEE signal processing letters*, *14*(12), 936–939.
- Roach, B. J. & Mathalon, D. H. (2008). Event-related EEG time-frequency analysis: An overview of measures and an analysis of early gamma band phase locking in schizophrenia. *Schizophrenia Bulletin*, *34*(5), 907–926.
- Rosenblum, M., Pikovsky, A., Kurths, J., Schäfer, C., & Tass, P. A. (2001). Phase synchronization: From theory to data analysis. In F. Moss & S. Gielen (Eds.), *Handbook of biological physics: Neuro-informatics and neural modelling*, vol. 4 (pp. 279–321). Elsevier.
- Rosenblum, M., Tass, P., Kurths, J., Volkmann, J., Schnitzler, A., & Freund, H-J. (2000). Detection of phase locking from noisy data: Application to magnetoencephalography. In K. Lehnertz, C. E. Elger, J. Arnhold, & P. Grassberger (Eds.), *Proceedings of the workshop on chaos in brain* (pp. 34–51). World Scientific.
TIME-FREQUENCY DECOMPOSITION METHODS 87
- Rutkowski, T. M., Mandic, D. P., Cichocki, A., & Przybyszewski, A. W. (2008). EMD approach to multichannel EEG data-the amplitude and phase synchrony analysis technique. In D-S. Huang, D. C. Wunsch II, D. S. Levine, & K-H. Jo (Eds.), Proceedings of the international *conference on intelligent computing: Advanced intelligent computing theories and applications. With aspects of theoretical and methodological issues* (pp. 122–129). Springer.
- Salinas, E. & Sejnowski, T. J. (2001). Correlated neuronal activity and the flow of neural information. *Nature Reviews Neuroscience*, *2*(8), 539.
- Sieluzycki, C., Konig, R., Matysiak, A., Kus, R., Ircha, D., & Durka, P. J. (2008). Single-trial evoked brain responses modeled by multivariate matching pursuit. *IEEE Transactions on Biomedical Engineering*, *56*(1), 74–82.
- Sponheim, S. R., McGuire, K. A., Kang, S. S., Davenport, N. D., Aviyente, S., Bernat, E. M., & Lim, K. O. Evidence of disrupted functional connectivity in the brain after combat-related blast injury. *Neuroimage*, *54*, S21–S29, 2011.
- Sweeney-Reed, C. M. & Nasuto, S. J. (2007). A novel approach to the detection of synchronisation in EEG based on empirical mode decomposition. *Journal of Computational Neuroscience*, *23*(1), 79–111.
- Tağluk, M. E., Çakmak, E. D., & Karakaş, S. (2005). Analysis of the time-varying energy of brain responses to an oddball paradigm using short-term smoothed Wigner–Ville distribution. *Journal of Neuroscience Methods*, *143*(2), 197–208.
- Tanaka, T. & Mandic, D. P. (2007). Complex empirical mode decomposition. *IEEE Signal Processing Letters*, *14*(2), 101–104.
- Tropp, J. A. & Gilbert, A. C. (2007). Signal recovery from random measurements via orthogonal matching pursuit. *IEEE Transactions on Information Theory*, *53*(12), 4655–4666.
- Von Stein, A., Chiang, C., & König, P. (2000). Top-down processing mediated by interareal synchronization. *Proceedings of the National Academy of Sciences*, *97*(26), 14748–14753.
- Williams, N., Nasuto, S. J., & Saddy, J. D. (2011). Evaluation of empirical mode decomposition for event-related potential analysis. *EURASIP Journal on Advances in Signal Processing*, *2011*(1), 965237.
- Wu, C-H., Lee, P-L., Shu, C-H., Yang, C-Y., Lo, M-T., Chang, C-Y., & Hsieh, J-C. (2012). Empirical mode decomposition-based approach for intertrial analysis of olfactory eventrelated potential features. *Chemosensory Perception*, *5*(3–4), 280–291.
- Wu, Z. & Huang, N. E. (2009). Ensemble empirical mode decomposition: A noise-assisted data analysis method. *Advances in Adaptive Data Analysis*, *1*(1), 1–41.
- Yeung, N., Bogacz, R., Holroyd, C. B., & Cohen, J. D. (2004). Detection of synchronized oscillations in the electroencephalogram: An evaluation of methods. *Psychophysiology*, *41*(6), 822–832.
- Zhao, Y. L., Atlas, E., & Marks, R. J. (1990). The use of cone-shaped kernels for generalized time-frequency representations of nonstationary signals. *IEEE Transactions on Acoustics, Speech, and Signal Processing*, *38*(7), 1084–1091.
# [CHAPTER 5](#page-5-7)
# [TIME FREQUENCY ANALYSES](#page-5-7) [IN EVENT-REL ATED](#page-5-7) [POTENTIAL METHODOLOGIES](#page-5-7)
ANNA WEINBERG, PAIGE ETHRIDGE, BELEL AIT OUMEZIANE, AND DAN FOTI
### **5.1 Introduction**
Event-related potentials (ERPs) are powerful tools for measuring the dynamics of human brain activity, and they have been used for decades to measure sensory, cognitive, motor, and emotion-related processes—as well as individual differences in these processes—across the lifespan (Cohen, 2014; De Haan, 2013; Hajcak et al., 2012; Kappenman & Luck, 2016; Luck, 2014). ERPs are defined by voltage fluctuations in the ongoing electroencephalogram (EEG) that are time-locked to specific events. As we discuss further in the studies we describe, these events can be the onset of an external stimulus (e.g., a picture, tone, or feedback about performance), or the generation of motor response (e.g., a button press).
Typically, tasks are designed so that these events are repeated across multiple trials, which are then averaged within conditions, presumably canceling out substantial amounts of trial-level noise and yielding the "prototypical" waveform that is common across trials (Figure 5.1A shows an example waveform). Specific ERP components are then identified within these averaged waveforms, and they are quantified numerically as deviations from a pre-event baseline period. A component is defined "a set of voltage changes that are consistent with a single neural generator site and that systematically vary in amplitude across conditions, time, [and] individuals," (Luck, 2014, p. 68). Thus, an ERP component is a portion of the overall waveform—often, a peak deflection in the waveform—that captures the brain response (or set of processes) that are of interest. ERPs are typically described in terms of their amplitude (measured in
TIME FREQUENCY ANALYSES 89

**Figure 5.1** (A) Example data depicting how multiple underlying ERP components (left) contribute to the observed grand averaged ERP waveforms (middle), which are then compared across conditions (right). (B) ERPs elicited by feedback delivery on the social incentive delay task.
microvolts; µV), polarity (positive or negative), latency (measured in milliseconds; ms), and scalp topography (where on the scalp the component is maximal). Amplitude refers to the difference between activity occurring at some point following an event of interest and an average pre-event baseline period (e.g., 200 ms prior to stimulus onset), and latency refers to the time from stimulus onset to some specific peak activity. Naming 90 ANNA WEINBERG, PAIGE ETHRIDGE, BELEL AIT OUMEZIANE, and DAN FOTI
conventions then frequently reflect both the polarity and latency of the component. Thus, the P3 is the third major positive-going peak in the ERP waveform after a stimulus is presented (and often peaks in the neighborhood of 300 ms, hence the common alternative name "P300"). At times, ERP components receive functionally descriptive names (e.g., the error-related negativity or ERN).
Because they measure the electrical activity of the brain, the speed of which approaches the speed of light, ERPs capture neural responses in the time-frame in which cognition occurs. This millisecond temporal resolution makes it theoretically possible to isolate dozens of individual neural processes that occur in even very close temporal proximity. ERPs have thus been particularly useful in studies requiring high temporal resolution to identify, for example, the transition from sensory-driven stimulus processing to higher-order cognitive functions (De Cesarei & Codispoti, 2006; Wiens et al., 2011), or specific cognitive or affective impairments in a given diagnostic group (Duncan et al., 2009; Kuperberg et al., 2018).
In comparison with other neuroimaging modalities, EEG techniques are wellsuited as assessment tools. EEG/ERP data collection is relatively efficient, economical, noninvasive, (Kappenman & Luck, 2016), and is well-tolerated by most participants across the developmental spectrum (De Haan, 2013). While ERP studies have traditionally been conducted in tightly controlled environments to minimize noise and electrical interference, advances in technology have allowed for progress in ERP data collection *outside* the laboratory and in remote field settings (Tarullo et al., 2017). Additionally, few contraindications exist for EEG research: for example, people with braces, pregnant women, and awake infants—all of whom are frequently excluded from MRI studies typically *can* participate in EEG studies, making it feasible to collect neuroimaging data from large and relatively diverse groups of participants. Finally, multiple studies over the years have explored the psychometric properties of ERPs and found them to be highly reliable measures of neural activity, comparable to other common assessment methods both in terms of internal consistency and test-retest reliability (Baldwin, Larson, & Clayson, 2015; Ethridge & Weinberg, 2018; Foti et al., 2016; Kujawa et al., 2018; Weinberg & Hajcak, 2011).
Naturally, these strengths are accompanied by a number of limitations. The assumption underlying measurement of ERP components in the time domain is that (a) each component represents distinct sensory and/or cognitive processes (or a small set of related processes), and (b) components reflect the activity of a single brain region (or a small network of closely related brain regions). In line with these assumptions, ERP components are typically scored based on where on the scalp and when in time specific peaks in the waveform occur, taking the average amplitude within a specified time window or the peak deflection (Figure 5.1A). This technique reduces the multidimensional EEG signal down to two dimensions, and has many advantages (Cohen, 2014; Luck, 2014). Yet the reality of neural activity is that multiple sensory, cognitive, affective, and motor processes can and do occur simultaneously. Because the observed trial-averaged waveform represents the sum of all activity measured at a particular site on the head within a particular time-window, ERPs representing these TIME FREQUENCY ANALYSES 91
unique processes are summed together in the waveform. Figure 5.1B shows how multiple observed components that overlap both spatially and temporally contribute to the grand averaged waveform. Traditional component-scored methods make it difficult to isolate the contribution each *underlying* component makes to the observed average ERP.
Additionally, the electrical signals captured by ERPs are conducted through the brain, meninges, skull, and scalp, and this signal is subject to spread as it seeks paths of low resistance; precise identification of primary neural contributors to any one component is therefore often difficult, particularly for brain regions that are relatively far from the scalp. Furthermore, neural activity recorded from an electrode exterior to the skull can reflect the simultaneous and summed activation of many, many thousands—even millions—of neurons (Luck, 2014). Combined with the difficulty of effectively isolating different components, this can often make source localization of time-domain ERP components a dicey proposition (Cohen, 2014).
Processing techniques that isolate unique sources of systematic variance within the trial-averaged waveform may allow for both more accurate identification of distinct neuroelectric signals and better description of their anatomical origins. These signals can be differentiated based on their temporal and spatial variance, as is done with typical time-window averages as well as more advanced techniques like principal component analysis (PCA) and independent components analysis (ICA; Dien, Spencer, & Donchin, 2003; Foti, Weinberg, Dien, & Hajcak, 2011; Spencer, Dien, & Donchin, 2001). Critically, distinct neural signals can also be differentiated based on their *spectral* properties. This is because the electrical activity measured by the EEG contains rhythmic oscillations. These oscillations reflect fluctuations in the activity of populations of neurons, and the different properties of these oscillations can be helpful in differentiating cognitive operations.
Oscillations are described by their *frequency, power*, and *phase*. *Frequency* describes the speed of the oscillation, or how many times a sine wave repeats, or cycles, in a given period of time, and is measured in hertz (Hz). A wave that repeats four times per second has a frequency of 4 Hz, a wave that repeats 50 times per second has a frequency of 50 Hz, and a wave that repeats once every two seconds has a frequency of 0.5 Hz. *Power* is a measure of how much energy is present in a frequency band and is represented as the amplitude (or height) of the peaks, squared. Finally, *phase* is measured in degrees, or radians, and is a measure of when in time any given part of the sine wave exists. EEG data, as well as the ERPs derived from these EEG data, are composed of oscillations at multiple frequencies, each present with different relative power at different time-points. Time-frequency techniques then attempt to deconvolve, or separate, these signals, to identify, for example, how much power is present at a given frequency at specific points in time.
There are many different signal processing techniques available for decomposing neuroelectric signals to describe the spectral characteristics of ERPs, including moving window Fourier transforms, wavelet transforms, and Cohen's class of time-frequency distributions. These all involve representing a given ERP waveform in terms of a set 92 ANNA WEINBERG, PAIGE ETHRIDGE, BELEL AIT OUMEZIANE, and DAN FOTI
of sine waves, each of which is characterized by different frequencies, phases, and amplitudes. Each technique uses different mathematical formulae to do so and makes different assumptions about the nature of the oscillatory signal presumed to underlie the ERP waveform (e.g., Bruns, 2004; Cohen, 2014; Luck, 2014). For a full discussion of these—and their relative strengths and weaknesses—see e.g., Aviyente, this volume, Keil & Thigpen, this volume? Voytek, this volume. However, a general caveat is that many of these techniques also involve a loss of temporal precision—one of the chief advantages of the ERP technique (Cohen, 2014; Luck, 2014)—though this matters more for some experiments than others, and there are techniques available to improve temporal precision (Aviyente et al., 2006).
In terms of their application to ERPs, time-frequency techniques are particularly useful when the signals overlap *both* temporally and spatially, therefore making these signals indistinguishable in the time domain (Bernat, Malone, Williams, Patrick, & Iacono, 2007; Bernat, Nelson, Steele, Gehring, & Patrick, 2011; Bernat, Williams, & Gehring, 2005; Cohen, Elger, & Ranganath, 2007; Herrmann, Rach, Vosskuhl, & Strüber, 2014; Kolev, Demiralp, Yordanova, Ademoglu, & Isoglu-Alkaç, 1997). In such instances, assessment of the differing spectral characteristics of overlapping ERP components is useful for distinguishing multiple underlying processes that give rise to the observed waveform. Additionally, insofar as populations of neurons in different regions of the brain may fire at different frequencies, the time-frequency components identified in this way may correspond more closely to distinct sources underlying event-related brain activity (Foti, Weinberg, Bernat, & Proudfit, 2015).
In what follows, we review literature demonstrating the ways in which timefrequency signal processing techniques have been useful in shedding new light on several common ERP components, helping to answer research questions that would be difficult to address solely within the time domain. We focus here on the mismatch negativity (MMN), the P3, the error-related negativity (ERN), and the feedback-related negativity (FN)/reward positivity (RewP). We conclude with a practical example of how to apply time-frequency techniques to ERP data and present new analyses of some of our prior time-domain work with the FN/RewP.
### **5.2 The Mismatch Negativity (MMN)**
The temporal resolution of ERPs makes them well suited for studying the earliest stages of sensory processing. One widely studied sensory ERP component is the MMN, a neural index of change detection that is automatically elicited by a deviant stimulus presented within a repetitive sequence (Näätänen, 1995; Näätänen, Paavilainen, Rinne, & Alho, 2007). While the MMN can be elicited within any sensory modality, it is commonly studied as part of auditory processing. For example, within a sequence of repeating standard tones, the presentation of a tone that differs with regard to pitch, duration, or some other stimulus characteristics TIME FREQUENCY ANALYSES 93
will automatically elicit the MMN. The auditory MMN typically occurs between 150 and 250 ms following the deviant stimulus and is maximal at frontocentral electrodes, with a smaller positive-going potential often apparent at temporal/ mastoid electrodes. While MMN morphology is dependent upon the stimulus characteristics, studies generally indicate that the MMN emanates from a combination of activity in supratemporal and frontal cortical regions (i.e., "temporal" and "frontal" MMN subcomponents), likely related to pre-perceptual stimulus processing and involuntary attentional switch, respectively (Alho, 1995). In addition to the large basic neuroscience literature applying the MMN to the study of sensory functioning, individual differences in MMN amplitude have been examined with regard to cognitive decline in aging, and cognitive impairment in psychiatric disorders (Näätänen et al., 2011). For example, the MMN is reduced by approximately one standard deviation among individuals with schizophrenia (Umbricht & Krljes, 2005). This impact of schizophrenia on MMN amplitude is equivalent to approximately 30 years of cognitive aging (i.e., the MMN of an individual with schizophrenia at age 20 is comparable to that of a non-psychotic individual at age 50; (Kiang, Braff, Sprock, & Light, 2009). Overall, traditional time-domain analyses of MMN amplitude have been useful for examining the time course of early sensory processing and deficits therein.
Complementing these time-domain studies, time-frequency studies have been useful for isolating the temporal and frontal subcomponents of the MMN, as well as contextualizing individual differences in MMN amplitude. The frontal portion of the MMN has been linked primarily to an increase in theta power (i.e., the amplitude of theta waves across trials), whereas the temporal portion has been linked to theta *phase coherence* (i.e., the alignment of theta waves across trials; also see Chapter 9) but not to theta power (Fuentemilla, Marco-Pallarés, Münte, & Grau, 2008; Ko et al., 2012). Time-frequency approaches have also helped clarify the nature of impaired sensory processing in schizophrenia. While a reduced frontal MMN in schizophrenia is well-documented, there is some evidence from time-domain analyses that the temporal (mastoid) subcomponent may be less affected (Baldeweg, Klugman, Gruzelier, & Hirsch, 2002). Subsequent studies in schizophrenia have used time-frequency approaches to clarify how abnormal MMN amplitude is explained by alterations in theta power and phase coherence. For example, one study found that time-domain MMN amplitude was strongly correlated with frontal theta power among healthy controls but not among individuals with schizophrenia, suggesting a decoupling between these signals (Hong, Moran, Du, O'Donnell, & Summerfelt, 2012). Other work shows that reduced MMN in schizophrenia is characterized by reductions in both theta power and phase coherence, with differential deficits based on the type of deviant stimulus (Lee et al., 2017). Thus, time-frequency decomposition of the MMN has been useful for teasing apart distinct neurological signals involved in sensory processing that would be difficult to capture within the time domain, with relevance to both basic science and clinical applications.
94 ANNA WEINBERG, PAIGE ETHRIDGE, BELEL AIT OUMEZIANE, and DAN FOTI
### **5.3 The P3**
The P3 was first reported by Sutton and colleagues (1965) and has since been among the most well-researched components in the ERP literature (Polich, 2012). It is among the canonical ERP components in that it is commonly observed across a wide range of stimuli and laboratory tasks, generally manifesting as the third major positivegoing deflection in the waveform and maximal at parietal electrodes. A P3 is typically elicited by stimuli that are relatively salient in the local context due to being infrequent, unexpected, or because they are designated "targets" that are task-relevant. Thus, the P3 is often present within the waveform for most ERP studies, even if it is not the component of primary interest. When the P3 is among the primary outcomes measures, one of the most common laboratory paradigms used is the "oddball" task (Donchin, Ritter, & McCallum, 1978). During an oddball task, participants are asked to respond to or otherwise keep track of a designated target stimulus and otherwise disregard other non-target stimuli (i.e., standard stimuli). In the case of a two-stimulus, auditory oddball task, for example, two different tones may be presented within an ongoing sequence, with differential likelihood (e.g., 80% for standards, 20% for targets). Participants are required to distinguish between these tones by responding to the occurrence of the target (e.g., button press or mentally counting) and not responding to the standard (Polich & Kok, 1995). Discriminating this infrequent target stimulus from the frequently occurring standard elicits a robust P3, which is increased (i.e., more positive) for the target vs. standard stimuli (Polich, 2012). Many studies also distinguish between the P3a and P3b subcomponents, which are clearly differentiated on three-stimuli oddball tasks which include frequent standard, infrequent target, and infrequent novel stimuli (i.e., a third stimulus type that is novel and task-irrelevant). In this case, the classic parietal P3 in response to target stimuli is referred to as the P3b, in order to distinguish it from an overlapping, frontocentral positivity to novel stimuli that is referred to as the P3a, (or Novelty P3; Simons, Graham, Miles, & Chen, 2001; N. Squires, Squires, & Hillyard, 1975). Broadly, the P3a is thought to reflect frontal lobe functioning in response to novelty, whereas the P3/P3b is thought to reflect temporal-parietal brain activity associated with attention and memory processing (Polich, 2007). For the remainder of this chapter, we generally use the term "P3" rather than "P3b."
Some theoretical accounts of the P3 within the oddball task posit that it captures the updating of an individual's mental representation prompted by incoming stimuli (i.e., Context Updating Theory; Donchin, 1981). Following an initial sensory input, it is thought that an attention-driven comparison between the current stimulus and previous mental representation in working memory is made. If no change in stimulus attributes have been distinguished, the prior mental representation or "schema" of the stimulus is maintained, thereby evoking sensory potentials. However, when a new stimulus attribute is perceived (e.g., a target) the mental representation of the stimulus context in working memory is updated to elicit the P3 (Donchin et al., 1986). TIME FREQUENCY ANALYSES 95
P3 amplitude has been shown to be influenced by a number of factors, including cognitive load demands (i.e., reduced P3 amplitude when under high cognitive load) and target stimulus probability (i.e., increased P3 amplitude to relatively rare stimuli). For example, people who performed a primary task with varying cognitive demands while also engaging in a secondary oddball task showed that increasing the primary tasks' difficulty attenuated P3 amplitude to targets on the oddball task (Isreal, Chesney, Wickens, & Donchin, 1980; Wickens, Kramer, Vanasse, & Donchin, 1983). Furthermore, detecting a target from a standard stimulus within the oddball paradigm elicits a robust P3 amplitude that potentiates as the global and local sequence probability for the target decreases (Duncan‐Johnson & Donchin, 1977; K. Squires, Wickens, Squires, & Donchin, 1976).
While there is a long history of examining P3 amplitude using traditional timedomain techniques, studies have also applied time-frequency techniques to decompose spectral properties of the P3. This is relevant in part because, in comparison to standard stimuli, target stimuli on an oddball task often elicit broad modulation of the ERP waveform that spans the P2-N2-P3-Slow Wave complex. Thus, the P3 occurs in the context of these other, overlapping neural signals that are also sensitive to stimulus properties, and for some questions it may be helpful to isolate the unique portions of the waveform that reflect context updating vs. other aspects of stimulus processing. Initial work in this domain showed that the oddball response is comprised of a progression from theta- to delta-band activity (Başar-Eroglu, Başar, Demiralp, & Schürmann, 1992; Kolev et al., 1997). Subsequent analyses applied principal components analyses to time-frequency plots in order to isolate a specific spectral subcomponent. The oddball response is characterized by an early, low-frequency component (1 Hz at 150 ms), followed by multiple delta-theta responses corresponding to the rise and peak of the time-domain P3 (1–3 Hz, from 400 to 600 ms), and ultimately resolving with a second low-frequency component (1 Hz from 600 to 800 ms) (Bernat et al., 2007).
Decomposing the oddball response in this manner has also been fruitful for clarifying the nature of individual differences in P3 amplitude in clinical populations. For example, it is well-established that time-domain P3 amplitude is reduced among individuals with externalizing psychopathology, such as alcohol use disorder (Polich, Pollock, & Bloom, 1994). In one study examining a clinically heterogeneous community sample, reduced time-domain P3 was common across conduct disorder, attention-deficit/hyperactivity disorder, oppositional defiant disorder, and substance use disorder (Gilmore, Malone, Bernat, & Iacono, 2010). As expected, the diagnostic groups were also generally associated with reduced power in multiple spectral subcomponents spanning 0.5–3 Hz and 200–900 ms. Critically, reduced power in a specific delta subcomponent (1 Hz, 400–600) differentiated the externalizing groups from controls, even after considering time-domain P3 amplitude. That is, this precise spectral subcomponent exhibited a stronger relationship with the clinical phenotype than the time-domain P3, which by definition is a composite of these multiple spectral subcomponents. Other work has examined reduced P3 amplitude in schizophrenia, which is well-documented (Jeon & Polich, 2003). Incorporating time-frequency analyses, however, showed that *total* deltaband activity to oddball stimuli (including phase-locked and non-phase-locked) is 96 ANNA WEINBERG, PAIGE ETHRIDGE, BELEL AIT OUMEZIANE, and DAN FOTI
intact among individuals with schizophrenia (Ergen, Marbach, Brand, Başar-Eroğlu, & Demiralp, 2008). This has potentially important implications for the interpretation of reduced time-domain P3: rather than a reduced neural response per se, the time-frequency analyses suggest that schizophrenia may be characterized by greater temporal jitter in the neural response, which manifests as a reduced peak in the trialaveraged waveform. Together, these studies show how a reduced P3 amplitude in clinical populations can be explained by multiple abnormalities in the neural signal, which are not readily apparent in the time domain.
## **5.4 The Error-Related Negativity (ERN)**
Rapidly identifying the mistakes that we make and altering our behavior in response to these errors is critical for adaptive functioning. The error-related negativity (ERN; also referred to as the error negativity or Ne) is an ERP component that has commonly been used to study neural processes associated with identifying and adapting to errors (Falkenstein, Hohnsbein, Hoormann, & Blanke, 1991; Gehring, Goss, Coles, Meyer, & Donchin, 1993). The ERN is a response-locked ERP often elicited in speeded reaction tasks that peaks approximately 100 ms following erroneous responses, is maximal at frontocentral electrode sites, and is thought to be generated in medial frontal cortex regions including the anterior cingulate cortex (ACC; for reviews see Gehring et al., 2011; Holroyd & Coles, 2002; Olvet & Hajcak, 2008). Time-frequency analyses have contributed to our knowledge of the unique structure of the ERN (Bernat et al., 2005; Munneke, Nap, Schippers, & Cohen, 2015; Riesel, Weinberg, Moran, & Hajcak, 2012; Yordanova, Falkenstein, Hohnsbein, & Kolev, 2004), have elucidated possible mechanisms by which it is generated (Luu, Tucker, & Makeig, 2004; Trujillo & Allen, 2007), and have provided empirical support for some existing theories of its functional significance (Cavanagh, Cohen, & Allen, 2009; Cavanagh, Zambrano‐Vazquez, & Allen, 2012; Luu & Tucker, 2001; Luu, Tucker, Derryberry, Reed, & Poulsen, 2003).
With regard to the structure of the component, time-frequency analyses have identified how the ERN is both linked to, and separable from, other related ERP components (Cavanagh et al., 2012; Di Gregorio, Maier, & Steinhauser, 2018; Gehring & Willoughby, 2004; Steele et al., 2016; Yordanova et al., 2004). For instance, it has been debated whether neural responses to errors (ERN) and to correct responses (correctrelated negativity; CRN or Nc), which overlap in time and scalp topography, reflect the same or distinct processes (Vidal, Hasbroucq, Grapperon, & Bonnet, 2000). While evidence indicates that the ERN and CRN demonstrate similar characteristics in the time-domain, frequency analyses have identified error-specific signals with unique scalp topographies (Yordanova et al., 2004), suggesting that the ERN and CRN are not identical processes and may have distinct neural generators. Specifically, Yordanova and TIME FREQUENCY ANALYSES 97
colleagues (2004) identified a delta-frequency component (1.5–3.5 Hz) that was specific to erroneous responses, as well as a theta-frequency component (4–8 Hz) that emerged for both erroneous and correct responses but demonstrated different scalp topographies depending on accuracy and response side (left or right hand). Similarly, time-frequency analyses have been used to demonstrate distinctions between the ERN and the errorrelated positivity (Pe) by demonstrating that the Pe can emerge in the absence of an ERN (Di Gregorio et al., 2018; Steele et al., 2016), as well as between the ERN and the feedback negativity (FN, see Section 5.5) by identifying distinct scalp topographies of the ERN and FN (Gehring & Willoughby, 2004). Nevertheless, theta frequency activity that is common to several ERP components (ERN, CRN, FN, and N2) has been interpreted to mean that each of these ERPs reflects similar (though not identical) neural processes related to performance monitoring and behavioral control (Cavanagh & Shackman, 2015; Cavanagh et al., 2012).
Time-frequency analyses are also uniquely placed to enhance our understanding of the mechanisms by which the ERN is generated. The classic view of ERPs suggests that they reflect phasic bursts of neural activation, while more recently it has been suggested that ERPs might reflect phase-resetting of ongoing oscillatory activity (see Keil & Thigpen, this volume). Although some argue that time-frequency techniques cannot distinguish between these two hypotheses (Yeung, Bogacz, Holroyd, & Cohen, 2004; Yeung, Bogacz, Holroyd, Nieuwenhuis, & Cohen, 2007), evidence suggests that the ERN is best explained by the combination of an amplitude increase and phase-resetting (Trujillo & Allen, 2007). This is an important contribution, partly because understanding how the ERN is generated provides insight into its functional significance. For example, Cavanagh and colleagues (2009) suggested that theta oscillatory dynamics reflected in the ERN may represent a mechanism by which neural regions responsible for performance monitoring and for cognitive control communicate with each other (see Chapter 3 for a discussion of neural oscillations; Keil & Thigpen).
As with all of the ERPs discussed in this chapter, understanding how the ERN is associated with individual difference variables is an active area of research. Timewindow analyses of ERN responses have identified links between the ERN and multiple forms of psychopathology, including generalized anxiety disorder (GAD) (Weinberg, Olvet, & Hajcak, 2010), obsessive compulsive disorder (Endrass et al., 2010; Riesel, Kathmann, & Endrass, 2014), substance use disorder (Euser, Evans, Greaves-Lord, Huizink, & Franken, 2013), and depression (Weinberg, Liu, & Shankman, 2016). Timefrequency analyses have begun to meaningfully advance our understanding of such individual differences. For instance, Cavanagh and colleagues (2017) determined that error-related theta power was a unique predictor of GAD status over and above the time-window scored ERN, and when they included theta network dynamics in their model, they were able to classify clinical participants with an impressive 66% accuracy. These data suggest that time-frequency analyses may have a powerful role to play in using neural data to classify clinical populations. While time-frequency analyses have led to several critical advances in our understanding of the ERN, as noted here, this is likely to remain a fruitful avenue of continued study.
98 ANNA WEINBERG, PAIGE ETHRIDGE, BELEL AIT OUMEZIANE, and DAN FOTI
## **5.5 The Feedback Negativity (FN)/ Reward Positivity (RewP)**
In addition to endogenous performance monitoring, optimization of behavior depends on the ability to discriminate positive (e.g., monetary gain, correct performance feedback, positive interpersonal feedback) from negative (e.g., monetary losses, incorrect performance feedback, negative interpersonal feedback) external environmental feedback. A substantial body of research on neural discrimination of favorable vs. unfavorable feedback has used an ERP component called, variously, the feedback negativity (FN), the feedback-related negativity (FRN), or the reward positivity (RewP) (Foti & Weinberg, 2018; Foti et al., 2011; Hajcak, Moser, Holroyd, & Simons, 2006; Holroyd, Nieuwenhuis, Yeung, & Cohen, 2003; Miltner, Braun, & Coles, 1997). This component peaks approximately 250–300 ms at frontocentral recording sites following the presentation of feedback (Miltner et al., 1997), and has often been studied in the context of laboratory gambling tasks, in which individuals make responses in order to win or lose money on each trial. Feedback indicating monetary gains, losses, or non-gains is presented following response selection.
Traditionally, the FN/RewP was viewed as a negative-going component (thus the emphasis on "negativity" in the name) and a member of a broader class of medial-frontal negativities (MFNs) that includes the ERN (Gehring & Willoughby, 2004; Miltner et al., 1997). This negative peak, which like other MFNs has been thought to be generated by the ACC (Gehring & Willoughby, 2002; Potts, Martin, Burton, & Montague, 2006) via phasic input from the midbrain dopamine system (Holroyd & Coles, 2002), was thought to be observed following unfavorable outcomes (e.g., feedback indicating monetary losses) and absent following favorable outcomes (e.g., feedback indicating monetary gain). This perspective suggests a binary differentiation of losses from non-losses, reflecting the activity of a single cognitive process (Hajcak et al., 2006; Kreussel et al., 2011). More recent data suggests, however, that the difference between neural responses to losses and gains may also be driven in part by a substantial positive-going deflection in the waveform elicited by favorable outcomes that is absent following unfavorable outcomes (i.e., the reward positivity; Baker & Holroyd, 2011; Bernat et al., 2011; Bogdan, Santesso, Fagerness, Perlis, & Pizzagalli, 2011; Carlson, Foti, Harmon-Jones, Mujica-Parodi, & Hajcak, 2011; Foti et al., 2011; Harper, Olson, Nelson, & Bernat, 2011; Hewig et al., 2010; Holroyd, Krigolson, & Lee, 2011; Holroyd, Pakzad-Vaezi, & Krigolson, 2008).
A possible explanation for these conflicting views is that the trial-averaged component following feedback reflects the activity of two independent but overlapping processes: a) a negative deflection in the waveform, which is enhanced following loss feedback but not reward feedback, and b) a positive deflection that is enhanced following reward feedback and decreased following losses (e.g., Bernat, Nelson, & Baskin-Sommers, 2015; Bernat et al., 2011; Carlson et al., 2011; Foti et al., 2011). An increased (underlying) negative-going component and a decreased (underlying) positive-going component TIME FREQUENCY ANALYSES 99
might then summate to create the *observed* negative-going component following feedback indicating losses that had typically been observed in the time domain (i.e., the classic FN/FRN/MFN).
Studies using time-frequency methods to explore neural activity in this time-window have tended to bear this out, as there is evidence that activity in both the theta- and delta-bands make unique contributions to the amplitude of the FN/RewP (Bernat et al., 2015; Bernat et al., 2011). In particular, theta activity in this time range appears to be primarily sensitive to loss/negative outcomes, with losses eliciting enhanced activity compared to gains in this frequency range (Bernat, Nelson, Holroyd, Gehring, & Patrick, 2008; Bernat et al., 2011; Gheza, De Raedt, Baeken, & Pourtois, 2018; Harper et al., 2011; L. Nelson, Patrick, Collins, Lang, & Bernat, 2011; Olson, Harper, Golosheykin, Bernat, & Anokhin, 2011; Webb et al., 2017). Delta has more often been linked to activity in the time-range of the P3 that follows the FN/RewP at more parietal sites (Gehring & Willoughby, 2002; Holroyd & Coles, 2002; Miltner et al., 1997). However, there is increasing evidence that delta activity also underlies the observed reward positivity occurring in the time-range and spatial location of the FN/RewP (Bernat et al., 2015; Bernat et al., 2008; Foti, Weinberg, Bernat, & Proudfit, 2014; Harper et al., 2011). Indeed, delta activity in this time-range is enhanced for gains compared to losses (Bernat et al., 2015; Bernat et al., 2008; Bernat et al., 2011; Cavanagh, 2015; Cavanagh, Masters, Bath, & Frank, 2014; Foti, Weinberg, et al., 2014; Gheza et al., 2018; Harper et al., 2011; Leicht et al., 2013; L. Nelson et al., 2011; Olson et al., 2011; Pornpattananangkul & Nusslock, 2016; Webb et al., 2017), and appears to drive the reward positivity observed in the trialaveraged waveforms (Bernat et al., 2015; Foti et al., 2011; Harper et al., 2011).
The activity of these two frequency bands also appears to be dissociable, insofar as the differences between loss and gain activity in the theta and delta band tend to be at best weakly correlated (e.g., Bernat et al., 2015; Bernat et al., 2011; Foti, Weinberg, et al., 2014). Moreover, source analysis suggests unique generators, with loss-related theta localizing to the ACC and gain-related delta to a possible source in the basal ganglia (Foti, Weinberg, et al., 2014). Combined, these data suggest that changes in theta and delta are not yoked expressions of the same underlying process, but instead may represent distinct cognitive processes and contributions to the FN/RewP (Bernat et al., 2015; Bernat et al., 2008; Bernat et al., 2011; Gheza et al., 2018; Harper et al., 2011; Olson et al., 2011). Consistent with this, theta response to losses appears to reflect a relatively low-level response to negative outcomes that is frequently insensitive to stimulus parameters and experimental context (Bernat et al., 2015; Bernat et al., 2011; Harper et al., 2011; Watts, Bachman, & Bernat, 2017; Watts & Bernat, 2018). This increased theta (Section 5.4) appears to then act as a signal to recruit attentional and executive resources to respond to mistakes, novelty, and negative feedback (Aviyente, Tootell, & Bernat, 2017; Cavanagh & Frank, 2014; Cavanagh et al., 2012; Van Noordt, Campopiano, & Segalowitz, 2016; van Noordt, Desjardins, Gogo, Tekok-Kilic, & Segalowitz, 2017). In contrast, in monetary reward paradigms, delta appears sensitive not only to loss vs. gain distinctions, but also higher-level secondary stimulus attributes, such as magnitude (Bernat et al., 2015), context (Bernat et al., 2015; Watts & Bernat, 2018), expectancy violations (Cavanagh, 2015; 100 ANNA WEINBERG, PAIGE ETHRIDGE, BELEL AIT OUMEZIANE, and DAN FOTI
Gheza et al., 2018; Watts et al., 2017), and reward uncertainty (Gheza et al., 2018) and thus may reflect more elaborative processing of the feedback beyond the most salient dimension of the stimuli (see, however: Leicht et al., 2013).
Identification of dissociable and functionally distinct processes in the time-window of the FN/RewP has also proven to be useful in studies seeking to understand individual differences in neural responses to feedback, including describing developmental influences on more specific neural processes, as well as identifying specific cognitive-affective deficits in clinical samples. For instance, there is evidence from MRI research that brain regions supporting the neural response to rewards undergo considerable developmental changes from childhood through adolescence and into adulthood. In particular, fMRI studies tend to find an adolescent-specific peak in striatal activation to reward feedback (Braams, van Duijvenvoorde, Peper, & Crone, 2015; J. R. Cohen et al., 2010; Ernst et al., 2005; Galvan et al., 2006; Somerville, Hare, & Casey, 2011; Van Leijenhorst et al., 2009). Most studies examining developmental changes in the FN/RewP, however, have failed to find evidence for an adolescentspecific peak, or indeed even significant developmental changes (Kujawa et al., 2018; Larson, South, Krauskopf, Clawson, & Crowley, 2011; Lukie, Montazer-Hojat, & Holroyd, 2014; Santesso, Dzyundzyak, & Segalowitz, 2011); but see also (Arbel, McCarty, Goldman, Donchin, & Brumback, 2018). In a recent study of 8–17-year-old participants, however, Bowers and colleagues (2018) examined both time-domain ERPs and time-frequency-derived theta and delta band activity. They found that, consistent with previous work, the time-domain-scored RewP was not associated with participants' age. Yet, theta power—which was enhanced for losses relative to gains—decreased with age, whereas delta power—which was greater for gains than losses—increased. In a study investigating whether family history of psychopathology might influence these normative developmental effects, we also collected a sample of never-depressed daughters of mothers with or without a history of depression (Ethridge et al., 2021). In this sample, we found that the association between delta power and daughters' developmental stage differed depending on maternal risk status. For daughters of mothers who had never been depressed, increased development was associated with increases in delta power following rewards. For daughters of mothers with a history of depression, increased development was associated with *decreased* delta power following rewards, suggesting high-risk daughters may become increasingly vulnerable across the course of adolescence. This effect was not observed for power in the theta frequency.
Work identifying functional differences between delta and theta activation in response to external feedback has laid the foundation for identifying specific cognitive and affective deficits in various psychopathological groups. For instance, there is extensive data suggesting that individuals high on externalizing-proneness (including alcohol and substance use/abuse, rule-breaking, and personality measures) show broad and nonspecific amplitude reductions in multiple ERPs (Hall, Bernat, & Patrick, 2007; Polich et al., 1994). This work has been further clarified by time-frequency decompositions suggesting these individuals do not in fact show deficits related to theta power elicited TIME FREQUENCY ANALYSES 101
by loss feedback; instead, these group differences seem to be driven by reductions in delta activity elicited by rewarding feedback (Bernat et al., 2011).
A great deal of work has also examined the FN/RewP in individuals with depression or at risk for depression (including work from our own groups). Multiple previous studies employing monetary guessing tasks have reported that depressed participants as well as those at risk for depression are characterized by abnormal FN/ RewPs (Bress, Smith, Foti, Klein, & Hajcak, 2011; Foti, Carlson, Sauder, & Proudfit, 2014; Foti & Hajcak, 2009; Kujawa, Proudfit, & Klein, 2014; Weinberg, Liu, Hajcak, & Shankman, 2015; Weinberg & Shankman, 2016). However, because many of these studies measured the FN/RewP as a difference score, it is unclear whether these results reflect aberrant neural response to rewards, to losses, or to both. Time-frequency investigations have been helpful in clarifying the locus of dysfunction. For instance, in one study we worked on, greater symptoms of depression were associated specifically with more blunted reward-related delta—no such association was found with loss-related theta (Foti et al., 2015). Similarly, another study indicated that blunted delta activity following reward feedback prospectively predicted the onset of depression in an adolescent sample—independently of other risk factors (B. Nelson et al., 2018). We also found that stress exposure—an important predictor of depression specifically blunted reward-related delta, and not theta, power; and that decreased delta power prior to an acute stressor predicted heightened physiological responses to that stressor (Ethridge et al., 2020).
Additionally, reduced reward-related delta may be helpful in identifying distinct symptom profiles. A recent study found that, within a depressed group, symptoms of anxiety and depression showed dissociable correlations with punishment-elicited theta power and reward-elicited delta power (Cavanagh, Bismark, Frank, & Allen, 2018), such that symptoms of depression were uniquely associated with decreased reward-elicited delta power. In contrast, one study found depression to be associated with blunted midline theta modulation (Mueller, Panitz, Pizzagalli, Hermann, & Wacker, 2015), while Webb and colleagues (2017) found that depressed adolescents showed *increased* lossrelated theta, but no differences in gain-related delta. A theme across these studies is that the time-domain FN/RewP generally represents a composite of frontocentral theta- and delta-band activity. The relative contribution of these frequency bands to the observed ERP score, however, will be different across tasks, sample characteristics, and study contexts, such that a change in FN/RewP amplitude can be explained by modulation of theta activity, delta activity, or a combination of both—a question which timefrequency decompositions can answer directly.
### **5.6 Example: Social Reward Processing**
As a practical example of how to apply time-frequency analyses to averaged ERP data, we revisit recently published findings on social reward processing (Ait Oumeziane, 102 ANNA WEINBERG, PAIGE ETHRIDGE, BELEL AIT OUMEZIANE, and DAN FOTI
Schryer-Praga, & Foti, 2017). ERP data were collected from 27 adults during a social incentive delay task, a modified version of the commonly used monetary incentive delay task (Knutson, Westdorp, Kaiser, & Hommer, 2000; B. K. Novak, Novak, Lynam, & Foti, 2016; K. D. Novak & Foti, 2015). The task is designed to tease apart anticipatory and consummatory stages of reward processing. On each trial, participants are first presented with a cue indicating whether it is an incentive or neutral trial. On incentive trials, participants have the opportunity to earn a reward by rapidly responding to a target stimulus (and are punished for slow reaction times), whereas on neutral trials participants break even regardless of their reaction time. Following their behavioral response to the target stimulus, participants are then shown feedback indicating the result of that trial (i.e., win or loss on incentive trials, break-even on neutral trials). On the traditional monetary version of the task the rewards are nominal amounts of money, yet more recently a social reward version has been developed in which the "wins" are instead positive social feedback putatively administered by the experimenter. In a recent study, it was shown that social reward feedback elicits a RewP and feedback-P3 (described as such in order to differentiate it from the oddball P3, described earlier) that is of similar morphology and amplitude to monetary reward feedback (Ait Oumeziane et al., 2017). These original analyses focused exclusively on traditional time-domain approaches to scoring the RewP and feedback-P3. Here, we revisit these data using timefrequency analysis.
The time-domain ERP waveforms and scalp topographies are presented in Figure 5.1A. Consistent with previous research, social reward ("wins") elicited a more positive-going waveform than social punishment ("losses"). The RewP difference score (contrasting the valence of uncertain feedback: win vs. loss) peaked at 325 ms, whereas the feedback-P3 difference score (contrasting the salience of uncertain vs. certain feedback: win vs. break-even, loss vs. break-even) peaked at approximately 400 ms. A challenge in isolating the RewP and feedback-P3 in this case, however, is that the waveform to social rewards is modulated within a relatively broad time window of approximately 200–800 ms at centroparietal electrodes, thereby encompassing the P2-RewP-P3-Slow Wave complex. It is unclear whether the difference between conditions represents multiple, overlapping effects or is instead better interpreted as a single, sustained increase in the ERP waveform. These possibilities are difficult to disentangle using traditional time-window averages but can be addressed using timefrequency analysis. Building upon previous time-frequency decompositions of the RewP (Bernat et al., 2011; Foti et al., 2015), we sought to isolate three distinct neural responses:
- 1. RewP-delta: an increase in delta power to wins vs. losses at approximately 300 ms and at central electrodes;
- 2. FN-theta: an increase in theta power to losses vs. wins at approximately 300 ms and at frontocentral electrodes; and
- 3. Feedback-P3-delta: an increase in delta power to wins vs. break-even outcomes at approximately 400 ms and at parietal electrodes.
TIME FREQUENCY ANALYSES 103
For illustrative purposes, we focus here on the P3 to wins; a similar pattern of results was also observed for the P3 to losses.
Standard signal processing procedures were applied to the data, including rereferencing to the mastoid electrodes, filtering from 0.1–30 Hz, ocular correction, and artifact rejection (for details, see Ait Oumeziane et al., 2017). The continuous EEG was segmented relative to the onset of feedback stimuli using a relatively broad time window of −1500 to 1500 ms, allowing for edge artifacts (i.e., distortion of the signal near the edges of the window following time-frequency transform; note this is a broader time-window than is typical for most ERP research). ERP averages were created for each of the three conditions (win, loss, break-even), and then the timefrequency transform was applied. Complex Morlet wavelets were calculated within BrainVision Analyzer (Brain Products), using a frequency range of 0.5–20 Hz and linear steps of 0.25 Hz. A relatively narrow frequency range was chosen here due to the a priori focus on activity in the delta and theta bands, whereas a broader range could be chosen for more exploratory analyses. The Morlet parameter was set at c = 3.5 (i.e., 3.5 cycles in the wavelet), and wavelet functions were normalized using Gabor normalization. Baseline correction was performed for each wavelet layer using a baseline window of −500 to −300 ms; the average amplitude in the baseline window was subtracted from each time point in the layer. These time-frequency transforms were applied to the averaged ERP data for each subject and then averaged across subjects to create the grand averaged spectrogram.
Of interest were two contrasts: wins vs. losses, which ought to elicit reward-related delta (RewP) and loss-related theta (FN) from approximately 200–400 ms; and win vs. break even, which ought to elicit delta-band activity in the time range of the feedback-P3 (300–500 ms). The spectrogram for the win vs. loss contrast is presented in Figure 5.2. As expected, activity in the delta frequency band was increased for wins vs. losses (the red portion of the spectrogram within the delta band), which peaked at approximately 2.5 Hz and 295 ms. Overlapping with this response was an increase in activity within the theta frequency band for losses vs. wins (the blue portion of the spectrogram within the theta band), which peaked at approximately 5.25 Hz and at 235 ms. Both of these responses occurred within the time range of the FN/RewP but at distinct frequency bands, presenting the opportunity to extract separate scores for each. We scored the delta and theta responses by extracting wavelet layers centered at 2.5 Hz and 5.25 Hz, respectively. Wavelet layers yield a waveform representing power at that frequency band over time, which can then be scored by taking a time-window average of peak score akin to time-domain ERPs (Figure 5.2, right). We scored each response as the average power within a 50-ms window surrounding the peak of the win minus loss difference, which was somewhat different for each frequency band: 270–320 ms for delta and 210– 260 ms for theta. Notably, these wavelets each exhibited more focal scalp topographies than the time-domain FN/RewP, with maxima at frontocentral electrodes. To maintain consistency with the time-domain FN/RewP, we scored the delta and theta responses at electrode Cz. The effects of condition (win vs. loss) were significant for both delta (*t*(26) = 3.04, *p* < .01) and theta (*t*(26) = 3.11, *p* < .01). Critically, the difference scores
104 ANNA WEINBERG, PAIGE ETHRIDGE, BELEL AIT OUMEZIANE, and DAN FOTI

**Figure 5.2** Time-frequency analysis of the reward positivity elicited by the social incentive delay task. Top: The contrast of wins versus losses, isolating delta- and theta-band activity corresponding to the time-domain FN/RewP. Bottom: The contrast of wins versus break-even outcomes, isolating delta-band activity corresponding to the feedback-P3.
for delta and theta were also both significantly correlated with the time-domain RewP difference score (Table 5.1). As is common in the literature, the delta and theta effects were not significantly correlated with one another, further suggesting that they each capture a distinct portion of the FN/RewP.
The analogous spectrogram for the win vs. break-even contrast is presented in Figure 5.2. In comparison with the FN/RewP analyses, here we expected to find prominent delta-band activity corresponding to the feedback-P3. As seen in the spectrogram, activity in the delta band was indeed increased for wins vs. break-even outcomes, an effect which peaked at 1.75 Hz and at 365 ms. We extracted the wavelet layer at 1.75 Hz and scored this delta response as the average power from 340–390 ms. This wavelet exhibited a scalp topography highly similar to the time-domain feedback-P3, with a peak at centroparietal electrodes. To be consistent with our time-domain analyses, we scored this delta effect at electrode Pz. The increase in delta-band activity for win vs. break-even outcomes was statistically significant (*t*(26) = 7.90, *p* < .001), and the deltaband difference score was significantly correlated with the time-domain feedback-P3 difference score (Table 5.1).
TIME FREQUENCY ANALYSES 105
| reward processing | | | | | | |
|-------------------|-----------------|-------------------|-------------------|--------------------|----------------|--------------------|
| | | Reward Positivity | | | Feedback-P3 | |
| | | Time Domain | Delta
(2.5 Hz) | Theta
(5.25 Hz) | Time
Domain | Delta
(1.75 Hz) |
| FN/RewP | Time Domain | — | | | | |
| | Delta (2.5 Hz) | .39 | — | | | |
| | Theta (5.25 Hz) | −.40 | −.04 | — | | |
| Feedback-P3 | Time Domain | .47 | .14 | −.12 | — | |
| | Delta (1.75 Hz) | .16 | .00 | −.14 | .71 | — |
**Table 5.1 Correlations between time-domain and time-frequency scores of social**
Note: FN/RewP variables are the contrast of win vs. loss; feedback-P3 variables are the contrast of win vs. break-even. Coefficients are Spearman's rho. Values in bold are significant at *p* < .05.
It is notable that superior separation of the FN/RewP and feedback-P3 was achieved in this case by using time-frequency analyses as compared to traditional time-domain analyses. Specifically, the time-domain FN/RewP and feedback-P3 were significantly correlated with one another despite being scored at non-overlapping time windows (300–350 ms and 370–420 ms) and electrodes (Cz and Pz). This was not the case for the time-frequency measures: the FN-theta and RewP-delta scores were not significantly correlated with the time-domain feedback-P3 score, and P3-delta scores were not significantly correlated with the time-domain FN/RewP scores. We further tested this pattern of specificity using multiple regression, predicting each time-domain ERP from the three time-frequency variables. When entered as simultaneous predictors, timedomain FN/RewP amplitude was significantly predicted by a combination of RewPdelta (*β* = .46, *p* < .05) and FN-theta (*β* = −.38, *p* < .05), but not P3-delta (*β* = .11, *p* = .53). Conversely, time-domain feedback-P3 amplitude was significantly predicted only by P3-delta (*β* = .66, *p* < .001) and not by RewP-delta (*β* = .15, *p*= .33) or FN-theta (*β*= −.15, *p* = .28). Thus, time-frequency analysis facilitated the isolation of three distinct neural signals involved in social reward processing that would have been difficult to achieve solely within the time domain, where signal overlap is more problematic in this experimental context.
The example described shows how time-frequency analyses can aid in the interpretation of traditional ERP effects. In these data, positive social feedback modulated the ERP waveform in a time-range spanning the FN/RewP and P3, which overlapped with each other. The traditional time-domain approach of scoring these ERPs as the average amplitude within separate time windows could not adequately address the problem of component overlap. Time-frequency decomposition, on the other hand, was able to isolate three distinct signals: RewP-delta, FN-theta, and P3-delta. Similar to the time domain, these three signals were all sensitive to outcome type: RewP-delta and FN-theta 106 ANNA WEINBERG, PAIGE ETHRIDGE, BELEL AIT OUMEZIANE, and DAN FOTI
were modulated by outcome valence, and P3-delta was modulated by outcome certainty. In contrast with the time domain, however, these three signals achieved superior separation: RewP-delta and FN-theta each captured unique portions of the time-domain FN/RewP component, and they were unrelated to the time-domain P3 component. Likewise, P3-delta was strongly related to the time-domain P3 component but was unrelated to the time-domain FN/RewP component. Overall, time-frequency analyses help us rule out the interpretation that social reward broadly increases the ERP waveform in a nonspecific fashion; instead, this broad modulation clearly represents a composite of multiple neural signals. This also lays the groundwork for more precise characterization of individual differences, whereby we would expect specific associations with the timefrequency variables (which are relatively uncorrelated) as compared to the time-domain variables (which have substantial overlap).
Comprehensive descriptions of different methodological approaches are covered in other chapters (e.g., Chapter 4, this volume). However, one important step to consider is whether to conduct these analyses on single-trial or averaged data, as was done in our practical description earlier. As noted, ERPs are typically derived from averages composed of data from multiple trials. This practice reflects the typically low signalto-noise ratio of ERPs: the amplitude of many ERPs is no more than a few µV, while the amplitude of "background" neuroelectric signals (see chapter 6, this volume), other electrophysiological signals, and electrical interference from non-biological sources can be closer to tens of µV. When averaged together, this presumably randomly distributed noise cancels itself out, whereas the systematic signal, or ERPs, in the data will not, resulting in a legible ERP component. Single-trial analysis of ERP data typically requires relatively large-amplitude components (e.g., the P3). However, time-frequency techniques can in some cases make data more amenable to single-trial analysis, as electrical "noise" often has distinct spectral properties from the signal of interest. For instance, in studies interested in how error or feedback processing might influence triallevel adjustments of behavior, time-frequency techniques could allow the researcher to focus narrowly on theta and delta power on each trial, with higher frequency activity (e.g., alpha, 60-Hz line noise) isolated from these signals. Nonetheless, it is common practice to conduct time-frequency decompositions on averages of many trials. And because averages improve signal-to-noise ratio, they are also a helpful basis for identifying spectral power at different frequency ranges, particularly in exploratory research where the spectral characteristics of ERPs are less well-understood. As is often the case, the optimal method will depend on the research question.
### **5.7 Conclusions**
ERPs are powerful and flexible tools for understanding sensory, cognitive, and affective processes in the brain, but they are not without limitations. As discussed, timefrequency techniques can be helpful in addressing some of these limitations. They can TIME FREQUENCY ANALYSES 107
better leverage the multi-dimensional nature of EEG data—and, in principle, better represent the underlying neural signals—by accounting for not only voltage changes over time and site on the scalp, but also frequency, power, and phase, and may reveal multiple dissociable processes folded within the time-window-scored ERP. However, timefrequency techniques are not a magic bullet. As is discussed at length in other chapters, time-frequency decompositions can reduce temporal precision, a chief advantage of the ERP technique (though, as described in Chapter 4, there are techniques to minimize this loss). When applied to trial-averaged ERP data, time-frequency decompositions are best thought of conceptually as isolating potentially relevant ERP subcomponents. That is, it should be possible to "recreate" the pattern of observed ERP findings within the time-frequency domain, perhaps based on a combination of activity across multiple frequency bands. The time-frequency measures may be more precise than their timedomain counterparts to the extent that they isolate the relevant neural signal of interest, but in cases where there is no apparent modulation of the ERP waveform across experimental conditions, it is unlikely that time-frequency approaches will uncover "new" findings. Therefore, we encourage the reader to think of time-frequency decompositions applied to ERP data as the conceptual equivalent of deriving subscales within a selfreport questionnaire, which can often enhance the precision of measurement and help clarify the nature of associations with other measures. This is particularly useful where there are already well-established associations between a time-domain ERP and an external measure (e.g., clinical diagnosis, behavior, or personality trait), whereby timefrequency decompositions can help explain the nature of those associations. Thus, time-frequency analyses can be an effective approach for revisiting published data or extending the results of prior studies.
### **REFERENCES**
- Ait Oumeziane, B., Schryer-Praga, J., & Foti, D. (2017). "why don't they 'like'me more?": Comparing the time courses of social and monetary reward processing. *Neuropsychologia, 107*, 48–59.
- Alho, K. (1995). Cerebral generators of mismatch negativity (MMN) and its magnetic counterpart (MMNm) elicited by sound changes. *Ear and hearing, 16*(1), 38–51.
- Arbel, Y., McCarty, K. N., Goldman, M., Donchin, E., & Brumback, T. (2018). Developmental changes in the feedback related negativity from 8 to 14 years. *International Journal of Psychophysiology*.
- Aviyente, S., Tootell, A., & Bernat, E. M. (2017). Time-frequency phase-synchrony approaches with ERPs. *International Journal of Psychophysiology, 111*, 88–97.
- Baker, T., & Holroyd, C. (2011). Dissociated roles of the anterior cingulate cortex in reward and conflict processing as revealed by the feedback error-related negativity and N200. *Biological Psychology, 87*, 25–34.
- Baldeweg, T., Klugman, A., Gruzelier, J. H., & Hirsch, S. R. (2002). Impairment in frontal but not temporal components of mismatch negativity in schizophrenia. *International Journal of Psychophysiology, 43*(2), 111–122.
108 ANNA WEINBERG, PAIGE ETHRIDGE, BELEL AIT OUMEZIANE, and DAN FOTI
- Baldwin, S. A., Larson, M. J., & Clayson, P. E. (2015). The dependability of electrophysiological measurements of performance monitoring in a clinical sample: A generalizability and decision analysis of the ERN and P e. *Psychophysiology,52*(6), 790–800.
- Başar-Eroglu, C., Başar, E., Demiralp, T., & Schürmann, M. (1992). P300-response: possible psychophysiological correlates in delta and theta frequency channels. A review. *International Journal of Psychophysiology, 13*(2), 161–179.
- Bernat, E., Malone, S., Williams, W., Patrick, C., & Iacono, W. (2007). Decomposing delta, theta, and alpha time-frequency ERP activity from a visual oddball task using PCA. *International Journal of Psychophysiology, 64*(1), 62–74.
- Bernat, E., Nelson, L., & Baskin-Sommers, A. (2015). Time-Frequency Theta and Delta Measures Index Separable Components of Feedback Processing in a Gambling Task. *Psychophysiology,52*(5), 626–637.
- Bernat, E., Nelson, L., Holroyd, C., Gehring, W., & Patrick, C. (2008). *Separating cognitive processes with principal components analysis of EEG time-frequency distributions.* Paper presented at the Proceedings of SPIE.
- Bernat, E., Nelson, L., Steele, V., Gehring, W., & Patrick, C. (2011). Externalizing psychopathology and gain–loss feedback in a simulated gambling task: Dissociable components of brain response revealed by time-frequency analysis. *Journal of abnormal psychology, 120*(2), 352.
- Bernat, E., Williams, W., & Gehring, W. (2005). Decomposing ERP time-frequency energy using PCA. *Clinical Neurophysiology, 116*(6), 1314–1334.
- Bogdan, R., Santesso, D., Fagerness, J., Perlis, R., & Pizzagalli, D. (2011). Corticotropin-Releasing Hormone Receptor Type 1 (CRHR1) Genetic Variation and Stress Interact to Influence Reward Learning. *The Journal of Neuroscience,31*(37), 13246–13254.
- Bress, J., Smith, E., Foti, D., Klein, D., & Hajcak, G. (2011). Neural response to reward and depressive symptoms in late childhood to early adolescence. *Biological Psychology, 89*(1), 156– 162. doi:doi.org/10.1016/j.biopsycho.2011.10.004
- Carlson, J., Foti, D., Harmon-Jones, E., Mujica-Parodi, L., & Hajcak, G. (2011). The neural processing of rewards in the human striatum: Correlation of fMRI and event-related potentials. *NeuroImage,57*, 1608–1616. doi:10.1016/j.neuroimage.2011.05.037
- Cavanagh, J. F. (2015). Cortical delta activity reflects reward prediction error and related behavioral adjustments, but at different times. *NeuroImage, 110*, 205–216.
- Cavanagh, J. F., Bismark, A. W., Frank, M. J., & Allen, J. J. (2018). Multiple Dissociations between Comorbid Depression and Anxiety on Reward and Punishment Processing: Evidence from Computationally Informed EEG. *Computational Psychiatry*, 1–17.
- Cavanagh, J. F., Cohen, M. X., & Allen, J. J. B. (2009). Prelude to and resolution of an error: EEG phase synchrony reveals cognitive control dynamics during action monitoring. *Journal of Neuroscience, 29*(1), 98–105. doi:10.1523/jneurosci.4137-08.2009
- Cavanagh, J. F., & Frank, M. J. (2014). Frontal theta as a mechanism for cognitive control. *Trends in cognitive sciences, 18*(8), 414–421.
- Cavanagh, J. F., Masters, S. E., Bath, K., & Frank, M. J. (2014). Conflict acts as an implicit cost in reinforcement learning. *Nature communications,5*, 5394.
- Cavanagh, J. F., & Shackman, A. J. (2015). Frontal midline theta reflects anxiety and cognitive control: Meta-analytic evidence. *Journal of Physiology – Paris, 109*, 3–15. doi:10.1016/ j.jphysparis.2014.04.003
- Cavanagh, J. F., Zambrano‐Vazquez, L., & Allen, J. J. (2012). Theta lingua franca: A common mid‐frontal substrate for action monitoring processes. *Psychophysiology, 49*(2), 220–238.
- Cohen, M. (2014). *Analyzing neural time series data: theory and practice*: MIT press.
TIME FREQUENCY ANALYSES 109
- Cohen, M., Elger, C., & Ranganath, C. (2007). Reward expectation modulates feedback-related negativity and EEG spectra. *NeuroImage,35*(2), 968–978.
- Di Gregorio, F., Maier, M. E., & Steinhauser, M. (2018). Errors can elicit an error positivity in the absence of an error negativity: Evidence for independent systems of human error monitoring. *NeuroImage, 172*, 427–436. doi:10.1016/j.neuroimage.2018.01.081
- Dien, J., Spencer, K. M., & Donchin, E. (2003). Localization of the event-related potential novelty response as defined by principal components analysis. *Cognitive Brain Research, 17*(3), 637–650.
- Donchin, E. (1981). Surprise!. . . surprise? *Psychophysiology, 18*(5), 493–513.
- Donchin, E., Ritter, W., & McCallum, W. (1978). Cognitive psychophysiology: The endogenous components of the ERP. *Event-related brain potentials in man*, 349–411.
- Duncan‐Johnson, C. C., & Donchin, E. (1977). On quantifying surprise: The variation of event‐ related potentials with subjective probability. *Psychophysiology, 14*(5), 456–467.
- Endrass, T., Schuermann, B., Kaufmann, C., Spielberg, R., Kniesche, R., & Kathmann, N. (2010). Performance monitoring and error significance in patients with obsessivecompulsive disorder. *Biological Psychology, 84*, 257–263. [doi:10.1016/j.biopsycho.2010.02.002](http://doi:10.1016/j.biopsycho.2010.02.002%22)
- Ergen, M., Marbach, S., Brand, A., Başar-Eroğlu, C., & Demiralp, T. (2008). P3 and delta band responses in visual oddball paradigm in schizophrenia. *Neuroscience letters, 440*(3), 304–308.
- Ethridge, P., & Weinberg, A. (2018). Psychometric Properties of Neural Responses to Monetary and Social Rewards across Development. *International Journal of Psychophysiology, in press*.
- Euser, A. S., Evans, B. E., Greaves-Lord, K., Huizink, A. C., & Franken, I. H. A. (2013). Diminished error-related brain activity as a promising endophenotype for substance use disorders: Evidence from high-risk offspring. *Addiction Biology, 18*(970-984). doi:10.1111/ adb.12002
- Falkenstein, M., Hohnsbein, J., Hoormann, J., & Blanke, L. (1991). Effects of crossmodal divided attention on late ERP components: II. Error processing in choice reaction tasks. *Electroencephalography & Clinical Neurophysiology, 78*(6), 447–455. doi:10.1016/ 0013-4694(91)90062-9
- Foti, D., Carlson, J., Sauder, C., & Proudfit, G. (2014). Reward dysfunction in major depression: Multimodal neuroimaging evidence for refining the melancholic phenotype. *NeuroImage, 101*, 50–58.
- Foti, D., & Hajcak, G. (2009). Depression and reduced sensitivity to non-rewards versus rewards. *Biological Psychology*, *81*(1), 1–8. doi:10.1016/j.biopsycho.2008.12.004,
- Foti, D., Perlman, G., Hajcak, G., Mohanty, A., Jackson, F., & Kotov, R. (2016). Impaired error processing in late-phase psychosis: Four-year stability and relationships with negative symptoms. *Schizophrenia research, 176*(2-3), 520–526.
- Foti, D., & Weinberg, A. (2018). Reward and feedback processing: State of the field, best practices, and future directions. In.
- Foti, D., Weinberg, A., Bernat, E., & Proudfit, G. (2014). Anterior cingulate activity to monetary loss and basal ganglia activity to monetary gain uniquely contribute to the feedback negativity. *Clinical Neurophysiology*.
- Foti, D., Weinberg, A., Bernat, E., & Proudfit, G. (2015). Anterior cingulate activity to monetary loss and basal ganglia activity to monetary gain uniquely contribute to the feedback negativity. *Clin Neurophysiol, 126*(7), 1338–1347. doi:10.1016/j.clinph.2014.08.025
- Foti, D., Weinberg, A., Dien, J., & Hajcak, G. (2011). Event‐related potential activity in the basal ganglia differentiates rewards from nonrewards: Temporospatial principal components
110 ANNA WEINBERG, PAIGE ETHRIDGE, BELEL AIT OUMEZIANE, and DAN FOTI
- analysis and source localization of the feedback negativity. *Human brain mapping, 32*(12), 2207–2216.
- Fuentemilla, L., Marco-Pallarés, J., Münte, T., & Grau, C. (2008). Theta EEG oscillatory activity and auditory change detection. *Brain research, 1220*, 93–101.
- Gehring, W., Goss, B., Coles, M. G. H., Meyer, D. E., & Donchin, E. (1993). A neural system for error detection and compensation. *Psychological Science, 4*(6), 385–390. doi:10.1111/j.1467- 9280.1993.tb00586.x
- Gehring, W., Liu, Y., Orr, J. M., & Carp, J. (Eds.). (2011). *The error-related negativity (ERN/Ne)*. New York, NY: Oxford University Press.
- Gehring, W., & Willoughby, A. (2002). The medial frontal cortex and the rapid processing of monetary gains and losses. *Science, 295*(5563), 2279–2282. doi:10.1126/ science.1066893
- Gehring, W., & Willoughby, A. (2004). Are all medial frontal negativities created equal? Toward a richer empirical basis for theories of action monitoring. *Errors, conflicts, and the brain. Current opinions on performance monitoring, 14*, 20.
- Gheza, D., De Raedt, R., Baeken, C., & Pourtois, G. (2018). Integration of reward with cost anticipation during performance monitoring revealed by ERPs and EEG spectral perturbations. *NeuroImage, 173*, 153–164.
- Gilmore, C., Malone, S., Bernat, E., & Iacono, W. (2010). Relationship between the P3 event‐ related potential, its associated time‐frequency components, and externalizing psychopathology. *Psychophysiology, 47*(1), 123–132.
- Hajcak, G., Moser, J., Holroyd, C., & Simons, R. (2006). The feedback-related negativity reflects the binary evaluation of good versus bad outcomes. *Biological Psychology, 71*(2), 148–154. doi:10.1016/j.biopsycho.2005.04.001
- Hall, J. R., Bernat, E. M., & Patrick, C. J. (2007). Externalizing psychopathology and the errorrelated negativity. *Psychological science, 18*(4), 326–333.
- Harper, J., Olson, L., Nelson, L., & Bernat, E. (2011). *Delta-Band Reward Processing Occurring During the Feedback-Related Negativity (FRN)*. Poster presented at annual meeting of the Society for Psychophysiological Research. Boston, MA.
- Herrmann, C. S., Rach, S., Vosskuhl, J., & Strüber, D. (2014). Time–frequency analysis of eventrelated potentials: a brief tutorial. *Brain topography, 27*(4), 438–450.
- Hewig, J., Kretschmer, N., Trippe, R., Hecht, H., Coles, M., Holroyd, C., & Miltner, W. (2010). Hypersensitivity to reward in problem gamblers. *Biological psychiatry, 67*(8), 781–783.
- Holroyd, C., & Coles, M. (2002). The neural basis of human error processing: Reinforcement learning, dopamine, and the error-related negativity. *Psychological review, 109*(4), 679–709. doi:10.1037//0033-295X.109.4.67
- Holroyd, C., Krigolson, O., & Lee, S. (2011). Reward positivity elicited by predictive cues. *Neuroreport, 22*(5), 249.
- Holroyd, C., Nieuwenhuis, S., Yeung, N., & Cohen, J. (2003). Errors in reward prediction are reflected in the event-related brain potential. *Neuroreport*, *14*(18), 2481–2484. doi:10.10 97/ 01.wnr.0 0 0 0 0 9 9 6 01.414 03.a
- Holroyd, C., Pakzad-Vaezi, K., & Krigolson, O. (2008). The feedback correct-related positivity: sensitivity of the event-related brain potential to unexpected positive feedback. *Psychophysiology, 45*(5), 688–697. doi:10.1111/j.1469-8986.2008.00668.x
- Hong, L. E., Moran, L. V., Du, X., O'Donnell, P., & Summerfelt, A. (2012). Mismatch negativity and low frequency oscillations in schizophrenia families. *Clinical Neurophysiology, 123*(10), 1980–1988.
TIME FREQUENCY ANALYSES 111
- Isreal, J. B., Chesney, G. L., Wickens, C. D., & Donchin, E. (1980). P300 and tracking difficulty: Evidence for multiple resources in dual‐task performance. *Psychophysiology, 17*(3), 259–273.
- Jeon, Y. W., & Polich, J. (2003). Meta‐analysis of P300 and schizophrenia: Patients, paradigms, and practical implications. *Psychophysiology, 40*(5), 684–701.
- Kappenman, E. S., & Luck, S. J. (2016). Best practices for event-related potential research in clinical populations. *Biological Psychiatry: Cognitive Neuroscience and Neuroimaging, 1*(2), 110–115.
- Kiang, M., Braff, D. L., Sprock, J., & Light, G. A. (2009). The relationship between preattentive sensory processing deficits and age in schizophrenia patients. *Clinical Neurophysiology, 120*(11), 1949–1957.
- Knutson, B., Westdorp, A., Kaiser, E., & Hommer, D. (2000). FMRI visualization of brain activity during a monetary incentive delay task. *NeuroImage, 12*(1), 20–27.
- Ko, D., Kwon, S., Lee, G.-T., Im, C. H., Kim, K. H., & Jung, K.-Y. (2012). Theta oscillation related to the auditory discrimination process in mismatch negativity: oddball versus control paradigm. *Journal of Clinical Neurology, 8*(1), 35–42.
- Kolev, V., Demiralp, T., Yordanova, J., Ademoglu, A., & Isoglu-Alkaç, Ü. (1997). Time– frequency analysis reveals multiple functional components during oddball P300. *Neuroreport, 8*(8), 2061–2065.
- Kreussel, L., Hewig, J., Kretschmer, N., Hecht, H., Coles, M., & Miltner, W. (2011). The influence of the magnitude, probability, and valence of potential wins and losses on the amplitude of the feedback negativity. *Psychophysiology, 49*, 207–219. doi:10.1111/j.1469-8986.2011.01291.x
- Kujawa, A., Carroll, A., Mumper, E., Mukherjee, D., Kessel, E., Olino, T., . . . Klein, D. (2018). A longitudinal examination of event-related potentials sensitive to monetary reward and loss feedback from late childhood to middle adolescence. *International Journal of Psychophysiology, 132*, 323–330.
- Kujawa, A., Proudfit, G., & Klein, D. (2014). Neural reactivity to rewards and losses in offspring of mothers and fathers with histories of depressive and anxiety disorders. *Journal of abnormal psychology, 123*(2), 287.
- Larson, M. J., South, M., Krauskopf, E., Clawson, A., & Crowley, M. J. (2011). Feedback and reward processing in high-functioning autism. *Psychiatry research, 187*(1-2), 198–203.
- Lee, M., Sehatpour, P., Hoptman, M. J., Lakatos, P., Dias, E. C., Kantrowitz, J. T., . . . Javitt, D. C. (2017). Neural mechanisms of mismatch negativity dysfunction in schizophrenia. *Molecular psychiatry, 22*(11), 1585.
- Leicht, G., Troschütz, S., Andreou, C., Karamatskos, E., Ertl, M., Naber, D., & Mulert, C. (2013). Relationship between oscillatory neuronal activity during reward processing and trait impulsivity and sensation seeking. *PloS one, 8*(12), e83414.
- Luck, S. J. (2014). *An introduction to the event-related potential technique*: MIT press.
- Lukie, C. N., Montazer-Hojat, S., & Holroyd, C. B. (2014). Developmental changes in the reward positivity: An electrophysiological trajectory of reward processing. *Developmental cognitive neuroscience, 9*, 191–199.
- Luu, P., & Tucker, D. M. (2001). Regulating action: Alternating activation of midline frontal and motor cortical networks. *Clinical Neurophysiology, 112*(7), 1295–1306. doi:10.1016/ S1388-2457(01)00559-4
- Luu, P., Tucker, D. M., Derryberry, D., Reed, M., & Poulsen, C. (2003). Electrophysiological responses to errors and feedback in the process of action regulation. *Psychological Science, 14*(1), 47–53. doi:10.1111/1467-9280.01417
112 ANNA WEINBERG, PAIGE ETHRIDGE, BELEL AIT OUMEZIANE, and DAN FOTI
- Luu, P., Tucker, D. M., & Makeig, S. (2004). Frontal midline theta and the error-related negativity: Neurophysiological mechanisms of action regulation. *Clinical Neurophysiology, 115*, 1821–1835. doi:10.1016/j.clinph.2004.03.031
- Miltner, W., Braun, C., & Coles, M. (1997). Event-related brain potentials following incorrect feedback in a time-estimation task: Evidence for a "generic" neural system for error detection. *Journal of Cognitive Neuroscience, 9*(6), 788–798. doi:10.1162/jocn.1997.9.6.788
- Mueller, E. M., Panitz, C., Pizzagalli, D. A., Hermann, C., & Wacker, J. (2015). Midline theta dissociates agentic extraversion and anhedonic depression. *Personality and Individual Differences, 79*, 172–177.
- Munneke, G.-J., Nap, T. S., Schippers, E. E., & Cohen, M. X. (2015). A statistical comparison of EEG time- and time-frequency domain representations of error processing. *Brain Research, 1618*(222-230). doi:10.1016/j.brainres.2015.05.030
- Näätänen, R. (1995). The mismatch negativity: a powerful tool for cognitive neuroscience. *Ear and hearing, 16*(1), 6–18.
- Näätänen, R., Kujala, T., Kreegipuu, K., Carlson, S., Escera, C., Baldeweg, T., & Ponton, C. (2011). The mismatch negativity: an index of cognitive decline in neuropsychiatric and neurological diseases and in ageing. *Brain, 134*(12), 3435–3453.
- Näätänen, R., Paavilainen, P., Rinne, T., & Alho, K. (2007). The mismatch negativity (MMN) in basic research of central auditory processing: a review. *Clinical Neurophysiology, 118*(12), 2544–2590.
- Nelson, B., Infantolino, Z., Klein, D., Perlman, G., Kotov, R., & Hajcak, G. (2018). Timefrequency reward-related delta prospectively predicts the development of adolescent-onset depression. *Biological Psychiatry: Cognitive Neuroscience and Neuroimaging,3*(1), 41–49.
- Nelson, L., Patrick, C., Collins, P., Lang, A., & Bernat, E. (2011). Alcohol impairs brain reactivity to explicit loss feedback. *Psychopharmacology*, 1–10.
- Novak, B. K., Novak, K. D., Lynam, D. R., & Foti, D. (2016). Individual differences in the time course of reward processing: stage-specific links with depression and impulsivity. *Biological Psychology, 119*, 79–90.
- Novak, K. D., & Foti, D. (2015). Teasing apart the anticipatory and consummatory processing of monetary incentives: An event‐related potential study of reward dynamics. *Psychophysiology,52*(11), 1470–1482.
- Olson, L., Harper, J., Golosheykin, S., Bernat, E., & Anokhin, A. (2011). *Development of the Feedback Negativity in early adolescence: A longitudinal study of time-frequency theta and delta components.* Poster presented at the 2011 meeting of the Society for Psychophysiological Research.
- Olvet, D. M., & Hajcak, G. (2008). The error-related negativity (ERN) and psychopathology: Toward an endophenotype. *Clinical Psychology Review, 28*(8), 1343–1354. doi:10.1016/ j.cpr.2008.07.003
- Polich, J. (2007). Updating P300: an integrative theory of P3a and P3b. *Clinical Neurophysiology, 118*(10), 2128–2148.
- Polich, J. (2012). Neuropsychology of P300. *Oxford handbook of event-related potential components*, 159–188.
- Polich, J., & Kok, A. (1995). Cognitive and biological determinants of P300: an integrative review. *Biological Psychology, 41*(2), 103–146.
- Polich, J., Pollock, V., & Bloom, F. (1994). Meta-analysis of P300 amplitude from males at risk for alcoholism. *Psychological bulletin, 115*(1), 55.
TIME FREQUENCY ANALYSES 113
- Pornpattananangkul, N., & Nusslock, R. (2016). Willing to wait: Elevated reward-processing EEG activity associated with a greater preference for larger-but-delayed rewards. *Neuropsychologia, 91*, 141–162.
- Potts, G., Martin, L., Burton, P., & Montague, P. (2006). When things are better or worse than expected: the medial frontal cortex and the allocation of processing resources. *Journal of Cognitive Neuroscience, 18*(7), 1112–1119.
- Riesel, A., Kathmann, N., & Endrass, T. (2014). Overactive performance monitoring in obsessive-compulsive disorder is independent of symptom expression. *European Archives of Psychiatry and Clinical Neuroscience, 264*, 707–717. doi:10.1007/s00406-014-0499-3
- Riesel, A., Weinberg, A., Moran, T., & Hajcak, G. (2012). Time course of the error-potentiated startle and its relationship to error-related brain activity. *Journal of Psychophysiology, 27*(2), 51–59. doi:10.1027/0269-8803/a000093
- Santesso, D. L., Dzyundzyak, A., & Segalowitz, S. J. (2011). Age, sex and individual differences in punishment sensitivity: Factors influencing the feedback‐related negativity. *Psychophysiology, 48*(11), 1481–1489.
- Simons, R. F., Graham, F. K., Miles, M. A., & Chen, X. (2001). On the relationship of P3a and the Novelty-P3. *Biological Psychology,56*(3), 207–218.
- Spencer, K. M., Dien, J., & Donchin, E. (2001). Spatiotemporal analysis of the late ERP responses to deviant stimuli. *Psychophysiology,38*(2), 343–358.
- Squires, K., Wickens, C., Squires, N., & Donchin, E. (1976). The effect of stimulus sequence on the waveform of the cortical event-related potential. *Science, 193*(4258), 1142–1146.
- Squires, N., Squires, K., & Hillyard, S. (1975). Two varieties of long-latency positive waves evoked by unpredictable auditory stimuli in man. *Electroencephalography and clinical neurophysiology,38*(4), 387–401.
- Steele, V. R., Anderson, N. E., Claus, E. D., Bernat, E. M., Rao, V., Assaf, M., . . . Kiehl, K. A. (2016). Neuroimaging measures of error-processing: Extracting reliable signals from eventrelated potentials and functional magnetic resonance imaging. *NeuroImage, 132*, 247–260. doi:10.1016/j.neuroimage.2016.02.046
- Tarullo, A. R., Obradović, J., Keehn, B., Rasheed, M. A., Siyal, S., Nelson, C. A., & Yousafzai, A. K. (2017). Gamma power in rural Pakistani children: Links to executive function and verbal ability. *Developmental cognitive neuroscience, 26*, 1–8.
- Trujillo, L. T., & Allen, J. J. B. (2007). Theta EEG dynamics of the error-related negativity. *Clinical Neurophysiology, 118*, 645–668. doi:10.1016/j.clinph.2006.11.009
- Umbricht, D., & Krljes, S. (2005). Mismatch negativity in schizophrenia: a meta-analysis. *Schizophrenia research, 76*(1), 1–23.
- Van Noordt, S. J., Campopiano, A., & Segalowitz, S. J. (2016). A functional classification of medial frontal negativity ERPs: Theta oscillations and single subject effects. *Psychophysiology,53*(9), 1317–1334.
- van Noordt, S. J., Desjardins, J. A., Gogo, C. E., Tekok-Kilic, A., & Segalowitz, S. J. (2017). Cognitive control in the eye of the beholder: electrocortical theta and alpha modulation during response preparation in a cued saccade task. *NeuroImage, 145*, 82–95.
- Vidal, F., Hasbroucq, T., Grapperon, J., & Bonnet, M. (2000). Is the 'error negativity' specific to errors? *Biological Psychology,51*, 109–128. doi:10.1016/S0301-0511(99)00032-0
- Watts, A. T., Bachman, M. D., & Bernat, E. M. (2017). Expectancy effects in feedback processing are explained primarily by time-frequency delta not theta. *Biological Psychology, 129*, 242–252.
114 ANNA WEINBERG, PAIGE ETHRIDGE, BELEL AIT OUMEZIANE, and DAN FOTI
- Watts, A. T., & Bernat, E. M. (2018). Effects of reward context on feedback processing as indexed by time‐frequency analysis. *Psychophysiology*, e13195.
- Webb, C., Auerbach, R., Bondy, E., Stanton, C., Foti, D., & Pizzagalli, D. (2017). Abnormal neural responses to feedback in depressed adolescents. *Journal of abnormal psychology*, *126*(1), 19.
- Weinberg, A., & Hajcak, G. (2011). Longer term test–retest reliability of error‐related brain activity. *Psychophysiology, 48*(10), 1420–1425.
- Weinberg, A., Liu, H., Hajcak, G., & Shankman, S. (2015). Blunted neural response to rewards as a vulnerability factor for depression: Results from a family study. *Journal of abnormal psychology, 124*(4), 878.
- Weinberg, A., Liu, H., & Shankman, S. A. (2016). Blunted neural response to errors as a trait marker of melancholic depression. *Biological Psychology, 113*, 100–107. doi:10.1016/ j.biopsycho.2015.11.012
- Weinberg, A., Olvet, D. M., & Hajcak, G. (2010). Increased error-related brain activity in generalized anxiety disorder. *Biological Psychology, 85*, 472–480. doi:10.1016/ j.biopsycho.2010.09.011
- Weinberg, A., & Shankman, S. (2016). Blunted reward processing in remitted melancholic depression. *Clinical Psychological Science, in press*.
- Wickens, C., Kramer, A., Vanasse, L., & Donchin, E. (1983). Performance of concurrent tasks: a psychophysiological analysis of the reciprocity of information-processing resources. *Science, 221*(4615), 1080–1082.
- Yeung, N., Bogacz, R., Holroyd, C. B., & Cohen, J. D. (2004). Detection and synchronized oscillations in the electroencephalogram: An evaluation of methods. *Psychophysiology, 41*, 822–832. doi:10.1111/j.1469-8986.2004.00239.x
- Yeung, N., Bogacz, R., Holroyd, C. B., Nieuwenhuis, S., & Cohen, J. D. (2007). Theta phase resetting and the error-related negativity. *Psychophysiology, 44*, 39–49. doi:10.1111/ j.1469-8986.2006.00482.x
- Yordanova, J., Falkenstein, M., Hohnsbein, J., & Kolev, V. (2004). Parallel systems of error processing in the brain. *NeuroImage, 22*, 590–602. doi:10.1016/j.neuroimage.2004.01.040
# [CHAPTER 6](#page-5-8)
# [THE REL ATIONSHIP](#page-5-8) [BET WEEN EVOKED AND](#page-5-8) [INDUCED EEG/MEG](#page-5-8) [CHANGES](#page-5-8)
*Going Beyond Labels*
ALI MAZAHERI
### **6.1 INTRODUCTION**
For more than a century now researchers have been examining the electrical potentials and magnetic fields measured at the scalp to understand what is happening inside our brains when we perform various cognitive tasks. Researchers' primary approach is to characterize how the electro/magnetoencephalogram (E/MEG) signal changes in response to a particular "event", whether it be a button press or the onset of an auditory tone. These changes are historically labelled as either *evoked* or *induced*, with each label making assumptions about the origins of the change. The rationale behind evoked activity is that the brain produces a new response as a consequence of processing the event. This response is both time-locked and phase-locked to the experimental event. Induced activity, on the other hand, assumes that the brain has ongoing brain activity (i.e., activity that is always there) independent of any additive activity, and the event modulates this ongoing activity, in a time-locked, but not necessarily phase-locked manner. My hope is that the reader, through what I discuss in this chapter, will understand that these "labels" (while at times useful) can paint an incomplete picture of what is going on in the brain during cognitive processing. According to Andy Warhol, "The moment you label something, you take a step—I mean, you can never go back again to seeing it unlabeled". I further argue that for the field to move forward in gaining a richer understanding of 116 ALI MAZAHERI
the link between brain and cognition, we need to rethink how we label the different types of EEG responses.
## **6.2 EVOKED AND INDUCED: THE ASSUMPTION AND LABELS**
The evoked potential approach assumes a large component of the electrophysiological signals detected at the scalp is not related to the processing of the phenomena under investigation. Here, we need to average multiple trials (Figure 6.1) of EEG epochs centered around the experimental event to extract the "event"-related EEG signal, called the event-related potential (ERP) for EEG measurements, and event-related fields (ERF) for magnetoencephalography (MEG) measurements. The ERP/F reflects neural activity precisely *time* and *phase-locked* in response to an event. The peaks and troughs in the ERP waveform, which often follow a stereotypical temporal pattern of positive and negative voltage deflections, are classified as "components". Researchers theorize that these components map onto various task-relevant cognitive processes (Kappenman & Luck, 2011).
The evoked potential approach explicitly ignores the ongoing activity present in the EEG, as well as changes that although are time-locked to an experimental event, are not necessarily phase-locked to it. This is because of the rather critical assumption (and one this chapter spends considerable effort arguing against) that non-phase locked activity disappears in the averaging of event locked data epochs due to the deconstructive interference of random phases (Figure 6.1B). Capturing changes to the ongoing activity in EEG, as well as responses that are time-locked but not necessarily phaselocked requires averaging the time-frequency spectra of multiple EEG trials centered on the experimental event (Figure 6.1C). The time-frequency characterization of the ongoing EEG activity works particularly well since the signals contain rhythms, that is, oscillatory activity in characteristic frequency ranges (i.e., bands) including theta (3–7 Hz), alpha (8–13), beta (14–20 Hz), and gamma (30–100 Hz), with each band often exhibiting specific spatial distributions over the scalp (Siegel et al., 2012). The amplitude of an oscillation refers to the size of its (positive or negative) peak relative to some baseline.
The experimentally driven increase in the amplitude of a frequency band is often referred to as an event-related synchronization (ERS). The ERS terminology is based on the fact that when the activity of neurons becomes synchronized, the spatial summation of the post-synaptic potentials results in an amplitude increase (Pfurtscheller & Lopes da Silva, 1999). Conversely, desynchronization of the neuronal population firing results in the cancellation of post-synaptic potentials, and as such, a drop in oscillatory amplitude within a frequency band, sometimes referred to as event-related desynchronization (ERD). Much like the ERP components, the task-related changes
RELATIONSHIP BETWEEN EVOKED AND INDUCED EEG/MEG CHANGES 117

**Figure 6.1** (A) The onset of an event (e.g., auditory stimulus) can *evoke* activity that is both phase and time-locked to the onset of the event as well as *induce* activity that is time-locked but not phase-locked. (B) Time-domain averaging of multiple data epochs would result in the attenuation of the non-phase locked activity due to destructive interference. The activity remaining after the averaging reflects the brain's transient phase-locked response to an event.
Frequecy
118 ALI MAZAHERI
in oscillatory amplitudes map on to different facets of cognition (Siegel et al., 2012; Hanslmayr et al., 2016).
## **6.3 Going beyond Evoked and induced: the origin of the changes**
Besides the methodologically different approaches needed to extract each type of change, evoked and induced activity are also thought to reflect different processes occurring in the brain in response to an outside event. One rather now-classic framework (Pfurtscheller & Lopes da Silva, 1999) proposes that evoked changes (i.e., ERPs) are assumed to occur because of event locked changes of afferent activity into cortical neurons. On the other hand changes in oscillatory power of the ongoing EEG are hypothesized to emerge due to the interaction of neurons and interneurons that control the frequency components of the ongoing activity.
## **6.4 UNLabeling the labels: the relationship between evoked and ongoing activity**
The rather traditional view of evoked and ongoing activity (Figure 6.2) is that they reflect rather separate distinct neural phenomena. According to this view, the evoked activity that always has a consistent phase-locked to the onset of an experimental event rides on top of the ongoing activity. This is also sometimes referred to as the "additive view" of how ERPs are generated. Taken to the extreme, it is possible to view the evoked activity as completely independent of the ongoing activity (figure 6.3A). An alternate theory, referred to as a phase-resetting theory (figure 6.3B), postulates that there is no additive evoked activity elicited by the onset of an event, but that rather, the ongoing activity adjusts its phase to the onset of the experimental event (Makeig et al., 2002). Here, by averaging trials locked to the event, the ongoing activity before the onset of the event which has random phases is averaged out, while the event-related phase perturbed activity emerges as the evoked response.
Given that the predominant ongoing activity in the EEG signal is the alpha rhythm, it is believed that its phase-reset (or adjustment) to the onset of the experimental event plays a particular role in the formation of evoked responses (Makeig et al., 2002; Klimesch et al., 2007; Gruber et al., 2005; Hanslmayr et al., 2006). However, the phasereset of the ongoing rhythms is not exclusive to the alpha activity, with the theta rhythm
RELATIONSHIP BETWEEN EVOKED AND INDUCED EEG/MEG CHANGES 119

**Figure 6.2** Schema for the generation of induced (ERD/ERS) and evoked (ERP) activity whereby the former is highly frequency-specific.
Adapted from Pfurtscheller & Lopes da Silva, 1999.
also proposed to be involved in the formation of specific evoked responses such as the error-related negativity (Luu et al., 2004).
There has been a fair amount of controversy over whether phase-resetting can account for the formation of ERPs (Mazaheri & Jensen, 2006). The primary evidence for the occurrence of a phase-reset is that the phase of the ongoing activity at the time of the evoked response would be consistent across trials. However, the addition of a signal with a consistent phase across trials (i.e., a traditional additive evoked response) would also make the phase of the ongoing activity appear consistent across
### The two models of evoked response generation

**Figure 6.3** The additive versus phase-resetting theory of evoked response generation. (A) The additive theory assumes that evoked and ongoing activities are distinct neuronal phenomena. The experimental event "evokes" an additive, phase-locked response in each trial. (B) According to the phase-resetting view, the ongoing and evoked activity are the same neuronal phenomena, with no "new" additive response. Here the phases of the ongoing background oscillations become aligned (phase-reset or partial phase-reset) to an experimental event. The phase-locked (i.e., adjusted) oscillatory activity emerges as an evoked component when averaging the eventlocked trials.
120 ALI MAZAHERI

**Figure 6.4** Model of generation. The upper left of the figure shows 20 superimposed trials of a model evoked potential consisting of a single cycle of activity added to ongoing activity of the same frequency with variable phase and amplitude. Below is given the average evoked potential over 100 trials. At the upper right are the polar plots showing the phase distributions of the frequency of the evoked potential (and background activity) during the baseline and at the middle of the evoked potential. There is significant phase synchronization at the time of the evoked potential. At the bottom is a histogram of the power measurements in the middle of the evoked potential across the 100 trials (because of the Mortlet filtering effect this gives the maximum power). There is no significant change in power.
Reprinted by permission from Mazaheri & Picton, 2005.
trials (Figure 6.4) (Mazaheri & Picton, 2005; van Diepen & Mazaheri, 2018; Yeung et al., 2004).
Moreover, a rather convincing argument has been raised that the additive and phaseresetting model cannot be mathematically distinguished at the scalp level without invasive electrophysiological recordings (Telenczuk et al., 2010).
While the additive and phase-resetting theories offer a contradictory account of evoked and ongoing activity, they do share two common elements. Both theories assume across-trials averaging results in the attenuation of ongoing activity. However, this assumption has been challenged. There is now compelling evidence that the alpha rhythm, the dominant ongoing signal detected at the scalp, is nonsinusoidal, and across-trials averaging never really makes it go away. This observation greatly blurs the line between evoked and ongoing activity. Furthermore, it is important to note that the additive and phase-resetting debate has exclusively focused on the early-stimulus evoked responses (P1, N1, or the ERN) and fails to provide a complete account for the brain responses occurring 200 ms after an experimental event. These sustained responses (Figure 6.5), often lasting 100–200 ms, are believed to reflect neural processing related to high-level cognitive constructs ranging from working memory representation (Ikkai et al., 2010) to language comprehension (Kutas & Federmeier, 2011).
RELATIONSHIP BETWEEN EVOKED AND INDUCED EEG/MEG CHANGES 121
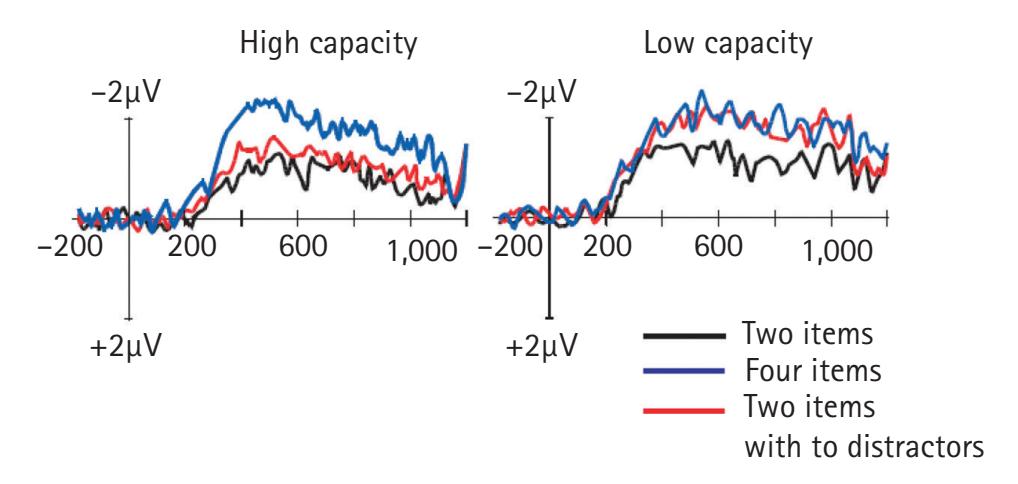
**Figure 6.5** Grand averaged ERP difference waves (contralateral activity minus ipsilateral activity) timelocked to the memory array averaged across the lateral occipital and posterior parietal electrode sites and divided across the high and low memory capacity groups.
From Vogel et al., 2005.
### **6.4.1 Amplitude Asymmetry/Baseline Shifts—A Unifying Perspective?**
Ongoing activity has been assumed to average out because it has traditionally been viewed to be amplitude symmetric in nature, that is, its peaks and troughs modulate at the same rate (Figure 6.6A).
While we are still seeking a complete understanding of the neural origin of the scalp electrophysiological signals (Cohen, 2017), the general consensus is that they are generated through synchronized post-synaptic current in the dendrites of pyramidal cells (Hämäläinen et al., 1993). Here the EEG reflects the potentials by these currents, while MEG captures the magnetic fields. For an oscillation to have symmetric amplitude fluctuations the intracellular currents propagating forward towards the soma (here let us arbitrarily designate this as the peak of the oscillation) must have the same magnitude as the current coming back from the soma (here assume the trough of the oscillation). However, given the asymmetric placement of channels responsible for the depolarization and repolarization current it is unlikely that the two currents would have the same magnitude when summed up across many synchronized neurons with the same orientation (Mazaheri & Jensen, 2008; Nikulin et al., 2007).
An alternative way to view ongoing activity is that is it amplitude asymmetric, with greater variability in amplitude fluctuations at the peak versus the trough (Figure 6.6B). One critical consequence of amplitude asymmetric ongoing activity is that it will not simply average out to zero when summed across trials. Moreover, any systematic suppression or enhancement of the amplitude of the ongoing activity time-locked to an event would result in the amplitude envelope of the ongoing activity emerging as a slow evoked response when averaging across trials.
122 ALI MAZAHERI

**Figure 6.6** The amplitude modulation of neuronal oscillatory activity is conventionally viewed as being symmetric at approximately zero. (B) We propose that the amplitude modulations of the oscillatory activity are asymmetric such that the peaks are more strongly modulated than the troughs. For the 10 Hz alpha activity, this could be explained by bouts of activity every ~100 ms. (C) The conventional view ignoring asymmetric modulations of oscillatory activity would mean that averaging across trials (the arrow representing the start of the evoked response) would not result in the generation of slow fields. (D) As a direct consequence of amplitude asymmetry, a depression (or increase) in alpha activity in response to a stimulus will result in the generation of slow fields when multiple trials are averaged. Adapted from Mazaheri and Jensen (2008).
### **6.4.2 Empirical Evidence Supporting Amplitude Asymmetry**
A seminal study by Nikulin and colleagues (2007) provided evidence that the ongoing alpha rhythm is "amplitude asymmetric", specifically referred by them as having a "zeromean". They went further to propose that a critical consequence of an amplitude asymmetric ongoing rhythm is that any systematic fluctuations in its amplitude would show up as slow responses (they referred to these as baseline shifts) when averaged across trials (Figure 6.7).
Following up Nikulin and colleagues, Mazaheri and Jensen (2008) developed a simple measure to quantify the amplitude of an oscillation by comparing the variance of its peaks with the variance of the troughs (see Figure 6.8).
Moreover, we were able to demonstrate that the degree of amplitude asymmetry of an oscillation is directly related to the amplitude of the evoked response generated by its modulation. Specifically, we presented a simple check-board stimulus across many trials, and then separated the trials into high amplitude of post-stimulus activity, and
RELATIONSHIP BETWEEN EVOKED AND INDUCED EEG/MEG CHANGES 123

**Figure 6.7** Baseline shifts in ongoing oscillations. Upper trace: spatially filtered (with independent component analysis) broadband signal from a channel above the right sensorimotor area during rest. Lower trace: the mean values in three time intervals. Clearly, there are baseline shifts in the ongoing activity associated with oscillations changing from large to small and back to large amplitude. If many epochs with similar amplitude dynamics are averaged, oscillatory patterns would disappear whereas the baseline shifts would remain leading to the appearance of an evoked response.
Nikulin et al., 2007.
low amplitude. We found that despite the stimulus being the same, the sorting of the trials based on alpha amplitude resulted in the formation of slow-evoked responses (Figure 6.9). Across participants the amplitude, and polarity of these slow responses was highly correlated with the direction of the amplitude asymmetry of the ongoing alpha activity. Thus we were able to demonstrate (albeit with simple grating stimuli) that it was (in principle) possible to form slow-evoked responses in the trial averaged EEG epochs if there were systematic changes in the amplitude of the ongoing alpha activity.
Mazaheri and Jensen (2010) proposed four prerequisites for linking modulations of oscillatory activity to evoked component generation.
- 1. The ongoing MEG/EEG oscillations must be modulated in amplitude by the stimuli or event.
- 2. This amplitude modulation of the ongoing activity must correlate with the time course of the evoked response (over trials or subjects).
- 3. The ongoing oscillations must have an amplitude asymmetry.
- 4. The magnitude and/or polarity of the amplitude asymmetry must relate to the amplitude and/or polarity of the evoked responses (over trials or subjects).
### **6.4.3 Making the Past as Important as the Future**
One rather intriguing consequence of having ongoing activity that never averages out is that the amplitude of the pre-event oscillatory activity could modulate the amplitude of the post-event-related potentials, when baseline subtracting the event-related potentials (Figure 6.10).
124 ALI MAZAHERI

**Figure 6.8** Various simulations in which surrogate signals were used to test the AFAindex. (A) The signal, s1(t), was designed to have an amplitude asymmetry. The amplitude modulation was determined by a slower signal A(t). Clearly the peaks (red dots) are more modulated than the troughs (blue dots) yielding a strong AFAindex. (B) The signal, s2(t), was designed such that the slow modulations, A(t), affected the alpha rhythm in a multiplicative manner. Thus peaks and troughs are modulated symmetrically over time yielding an AFAindex close to 0. (C) In signal s3(t) slow modulations were added to the alpha oscillations (DC-like offset of the signal). This affected peaks and troughs in the same direction producing an AFAindex close to 0.
Adapted from Mazaheri & Jensen, 2008.
Iemi and colleagues' (2019) comprehensive study systematically examined the relationship of pre-stimulus power of oscillatory, amplitude asymmetry, and the formation of evoked responses. In particular, Iemi and colleagues' (2019) focused on differentiating the impact of pre-stimulus functional inhibition (a sensory state being in a less-responsive state) from amplitude asymmetry on both the early and late sensory evoked responses.
Here, with functional inhibition, the authors were referring to the currently widely held view that an increase in alpha activity in a sensory system reflects its functional inhibition and consequently results in attenuated evoked responses (evidence recently reviewed in Van Diepen et al., 2019). They found that the early evoked (<0.200 s: e.g., the C1/N1 components) were indeed modulated by the amplitude of the pre-stimulus
RELATIONSHIP BETWEEN EVOKED AND INDUCED EEG/MEG CHANGES 125
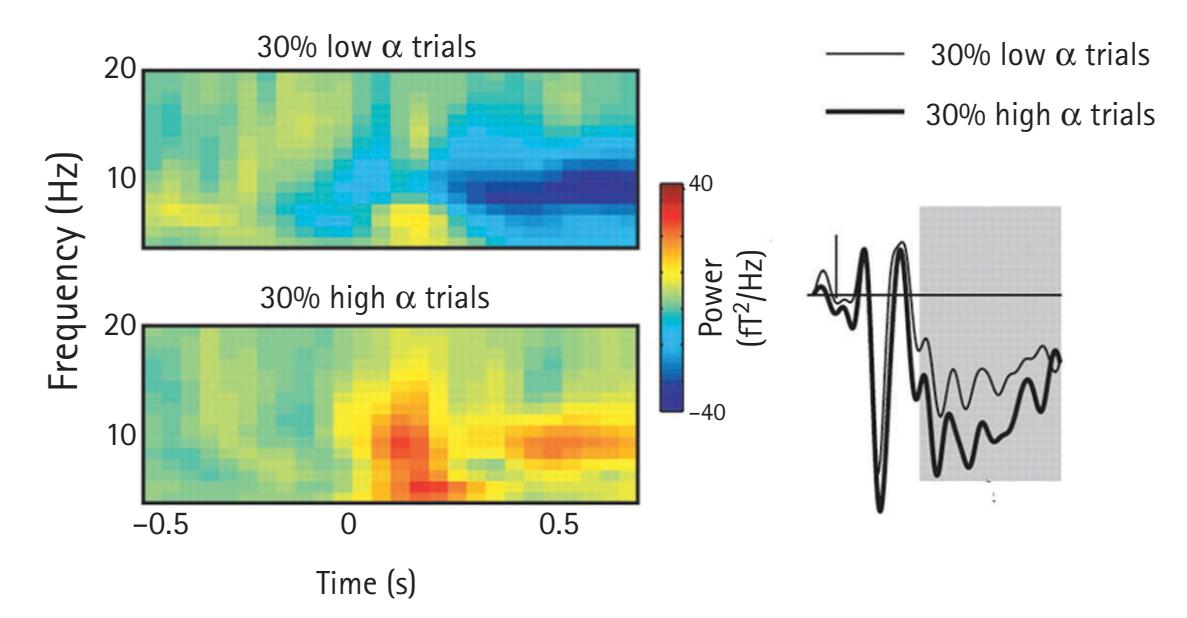
**Figure 6.9** Time-frequency representations of the trials with the 30% lowest and 30% highest modulations of alpha power (TFRs baseline corrected; −0.6 < t < −0.1 s) in a representative subject. The respective ERFs (right) reveal a clear difference in the sustained modulation with respect to low- (thin line) and high-alpha-power changes (thick line). Adapted from Mazaheri & Jensen, 2008.

**Figure 6.10** Ongoing activity (amplitude), event-related oscillations (ERS/ERD) and potentials (ERP) (see text for details).
The vertical line indicates stimulus onset, while the horizontal line indicates zero signal strength. Yellow and blue represent states of strong and weak prestimulus power, respectively. Reprinted from Iemi et al, 2019.
126 ALI MAZAHERI
alpha activity, independent of the direction of amplitude asymmetry. However, they found a strong relationship between amplitude asymmetry of the pre-stimulus activity and the late evoked components. These results taken together suggest high pre-stimulus alpha likely causes a suppression of early evoked responses since the neurons producing these responses are in an inhibited stated, while the amplitude of asymmetry property of alpha activity impacts the formation of the later slow evoked responses.
The results discussed so far strongly question the old dogma that ongoing and evoked activity are distinct independent neural phenomena. However, while the studies demonstrate that it is possible to generate slow evoked potentials through modulations of the amplitude of the ongoing activity (without any "new" additive activity), it is still unclear if this mechanism applies to cognitively relevant event-related responses.
### **6.4.4** *Can* **Amplitude Asymmetry Explain the Emergence of the Most Cognitive of ERPs?**
As mentioned earlier, the CDA is a slow sustained response proposed to reflect the neural representation of an item in working memory. It is often elicited through a paradigm where participants are presented with a bilateral array of colored squares and instructed to memorize the location of the items in the hemifield indicated by the arrow (i.e., test array). The success of memorizing the items in the test array is then subsequently assessed a second later through the presentation of another array that is either identical to the test array or missing one of the items. The CDA is derived by averaging epochs locked to the onset of the test array and subtracting the contralateral ERPs from the left.
The amplitude of the CDA is modulated by the number of items held in working memory (Vogel et al., 2005) However, the neural origins of the CDA are still rather a mystery. Moreover, the same paradigm has also been found to elicit robust modulations of alpha activity that are also modulated by the number of items held in working memory (Sauseng et al., 2009). In addition, just like the CDA, the degree of lateralized alpha modulation also seems to correlate with the individual differences in working memory. This suggests some overlap between the neural processes underlying the CDA and the alpha modulation.
A study published by Van Dijk and colleagues (2010) explored the link between changes in alpha activity and the CDA, and found them to be quite linked together. Specifically, they observed that both the degree of alpha suppression across individuals, as well as their degree of alpha amplitude asymmetry correlated very strongly with the amplitude of the CDA. Moreover, the alpha modulation and the CDA had a remarkably similar topography over the scalp. These observations taken together could suggest that the CDA and the alpha modulation during the period that the items are held in working memory are one and the same thing.
RELATIONSHIP BETWEEN EVOKED AND INDUCED EEG/MEG CHANGES 127
What are the consequences of re-labelling the CDA as a change in ongoing activity rather than a purely additive response? For one thing, this could have profound implications on how we believe the brain carries out working memory processes. As mentioned, one popular view of the role of alpha modulation in cognition is the suppression of task-irrelevant regions (Van Diepen et al., 2019). Thus, the CDA, rather than being an additive neural process involved in memory maintenance, could instead be reflecting the inhibition of task-irrelevant brain areas. Additionally, unifying ongoing and event-related activity has the potential to mechanistically account for some rather intriguing ERP findings, for which the origins of the responses remain a mystery. For example, a now-classic study (Otten et al., 2006) found that the amplitude of slow event-related potentials locked to the onset of a cue, but peaking before the onset of a word to be remembered, could predict if the word was later remembered. By linking the slow ERPs to the modulation of ongoing alpha activity, one simple interpretation of the observed difference between the remembered versus forgotten words could be that alpha activity is higher (i.e., the brain is in a more inhibited state) prior to the onset of forgotten words. This is indeed in line with several experiments observing pre-stimulus alpha oscillations to modulate perception (van Dijk et al., 2008) as well as reflect slips of sustained attention (Bengson et al., 2012).
### **6.4.5** *Does* **Amplitude Asymmetry Explain the Emergence of Most Cognitive of ERPs?**
While I hope that thus far this chapter demonstrates that modulations of ongoing activity that is amplitude asymmetric can produce sustained ERPs, the jury is still out on whether the ongoing and evoked activity, particularly the slow late components, are one and the same. Fukuda and colleagues (2015) challenged this view by observing that, while alpha modulation and CDA are tightly linked, they do appear to uniquely contribute to individual differences between working memory capacity. Specifically, the authors reasoned if the alpha suppression and CDA are two sides of the same neural phenomena they should also show the same relationship to individual differences in working memory performance. However, they found that each signal appeared to uniquely contribute to individual differences in working memory capacity.
More recently, Bae & Luck (2018) went further and used a decoding approach to investigate the specific roles alpha modulation and the slow sustained response could play in attention and working memory. They found modulations in the ongoing alpha activity to be associated with the spatial location of attended stimuli, whereas the amplitude and spatial distribution of the slow-sustained ERPs were sensitive to orientation. Interestingly, they proposed that the ERP and alpha modulation, while serving distinct roles, reflect attentional mechanisms that prevent interference, rather than the actual WM representation.
While these studies certainly do not rule out that the modulation of ongoing activity could be a significant contributor to the formation evoked responses, they do suggest 128 ALI MAZAHERI
the presence of additive activity involved in WM maintenance. In addition, the mechanism underlying amplitude asymmetry of alpha activity is also applicable to other frequency bands. This means that while the alpha rhythm is the predominant oscillation making up the ongoing activity, there could also be other rhythms present, such as the delta and theta rhythms (Stefanics et al., 2010), whose event-related modulation likely impacts the formation of evoked responses.
### **6.5 FINAL THOUGHTS**
I would certainly not advocate any researchers to dismiss the event-related averaging approach in exchange for looking at changes in the brain's ongoing activity. However, strictly viewing ongoing activity and evoked responses as separate unique entities is implicitly believing the brain was doing nothing before the onset of the experimental event. Such a view is particularly limited when it comes to trying to understand how the brain tries to make sense of the outside world.
As an example of how the brain endeavors to make sense of the world, one rather influential theory proposes that the brain is constantly making predictions about what is going to happen next (reviewed in detail in Friston, 2010). Specifically, this theory, referred to as "predictive coding", postulates that brain sets expectations and predictions about upcoming sensory input and then subsequently updates these expectations after the onset of the sensory input. Here, the discrepancy between the expectation and actual sensory input is referred to as prediction error. While evoked responses can reveal information about the degree of prediction error and the perceived mismatch between expectation and reality, they are not directly informative about the neurophysiology of the predictive processes themselves, since, by definition, the evoked response emerges *after* the sensory input. By removing the separate labels (going back to the Warhol quote) of evoked responses and ongoing activity, it is possible to get a richer, but at the same time more parsimonious, picture of the neural processes underlying cognition.
Finally, I paraphrase Warhol for one last time: I hope some of the mystery behind event-related responses and ongoing activity *is* gone, but the amazement *is* just starting.
### **REFERENCES**
Bae, G.-Y. & Luck, S. J. (2018). Dissociable decoding of spatial attention and working memory from EEG oscillations and sustained potentials. *The Journal of Neuroscience*, *38*(2), 409–422. Bengson, J. J., Mangun, G. R., & Mazaheri, A. (2012). The neural markers of an imminent failure of response inhibition. *NeuroImage*, *59*(2), 1534–1539.
Cohen, M. X. (2017). Where does EEG come from and what does it mean? *Trends in Neuroscience*, *40*(4), 208–218.
Friston, K. (2010). The free-energy principle: A unified brain theory? *Nature Reviews Neuroscience*, *11*(2), 127–138.
RELATIONSHIP BETWEEN EVOKED AND INDUCED EEG/MEG CHANGES 129
- Fukuda, K., Mance, I., & Vogel, E. K. (2015). α-power modulation and event-related slow wave provide dissociable correlates of visual working memory. *The Journal of Neuroscience*, *35*(41), 14009–14016.
- Gruber, W. R., Klimesch, W., Sauseng, P., & Doppelmayr, M. (2005). Alpha phase synchronization predicts P1 and N1 latency and amplitude size. *Cerebral Cortex*, *15*(4), 371–377.
- Hämäläinen, M., Hari, R., Ilmoniemi, R. J., Knuutila, J., & Lounasmaa, O. V. (1993). Magnetoencephalography: Theory, instrumentation, and applications to noninvasive studies of the working human brain. *Reviews of Modern Physics*, *65*, 413.
- Hanslmayr, S., Klimesch, W., Sauseng, P., Gruber, W., Doppelmayr, M., Freunberger, R., Pecherstorfer, T., & Birbaumer, N. (2006). Alpha phase reset contributes to the generation of ERPs. *Cerebral Cortex*, *17*(1), 1–8.
- Hanslmayr, S., Staresina, B. P., & Bowman, H. (2016). Oscillations and episodic memory: Addressing the synchronization/desynchronization conundrum. *Trends in Neuroscience*, *39*(1), 16–25.
- Iemi, L., Busch, N. A., Laudini, A., Haegens, S., Samaha, J., Villringer, A., & Nikulin, V. V. (2019). Multiple mechanisms link prestimulus neural oscillations to sensory responses. *Elife*, *8*, e43620.
- Ikkai, A., McCollough, A. W., & Vogel, E. K. (2010). Contralateral delay activity provides a neural measure of the number of representations in visual working memory. *Journal of Neurophysiology*, 103(4), 1963–1968.
- Kappenman, E. S., & Luck, S. J. (Eds.). (2011). *Oxford handbook of event-related potential components*. Oxford University Press.
- Klimesch, W., Sauseng, P., Hanslmayr, S., Gruber, W., & Freunberger, R. (2007). Event-related phase reorganization may explain evoked neural dynamics. *Neuroscience & Biobehavioral Reviews*, *31*(7), 1003–1016.
- Kutas, M. & Federmeier, K. D. (2011). Thirty years and counting: Finding meaning in the N400 component of the event-related brain potential (ERP). *Annual Review of Psychology*, *62*, 621–647.
- Luu, P., Tucker, D. M., & Makeig, S. (2004). Frontal midline theta and the error-related negativity: neurophysiological mechanisms of action regulation. *Clinical Neurophysiology*, *115*(8), 1821–1835.
- Makeig, S., Westerfield, M., Jung, T. P., Enghoff, S., Townsend, J., Courchesne, E., & Sejnowski, T. J. (2002). Dynamic brain sources of visual evoked responses. *Science*, *295*(5555), 690–694.
- Mazaheri, A. & Jensen, O. (2006). Posterior α activity is not phase-reset by visual stimuli. *Proceedings of the National Academy of Sciences of the United States of America*, *103*(8), 2948–2952.
- Mazaheri, A. & Jensen, O. (2008). Asymmetric amplitude modulations of brain oscillations generate slow evoked responses. *The Journal of Neuroscience*, *28*(31), 7781–7787.
- Mazaheri, A. & Jensen, O. (2010). Rhythmic pulsing: Linking ongoing brain activity with evoked responses. *Frontiers in Human Neuroscience* [online], *4*(177). doi: 10.3389/ fnhum.2010.00177
- Mazaheri, A. & Picton, T. W. (2005). EEG spectral dynamics during discrimination of auditory and visual targets. *Brain Research Cognitive Brain Research*, *24*(1), 81–96.
- Nikulin, V. V., Linkenkaer-Hansen, K., Nolte, G., Lemm, S., Müller, K. R., Ilmoniemi, R. J., & Curio, G. (2007). A novel mechanism for evoked responses in the human brain. *European Journal of Neuroscience*, *25*(10), 3146–3154.
- Otten, L. J., Quayle, A. H., Akram, S., Ditewig, T. A., & Rugg, M. D. (2006). Brain activity before an event predicts later recollection. *Nature Neuroscience*, *9*(4), 489–491.
130 ALI MAZAHERI
- Pfurtscheller, G. & Lopes da Silva, F. H. (1999). Event-related EEG/MEG synchronization and desynchronization: Basic principles. *Clinical Neurophysiology*, *110*(11), 1842–1857.
- Sauseng, P., Klimesch, W., Heise, K. F., Gruber, W. R., Holz, E., Karim, A. A., Glennon, M., . . . Hummel, F. C. (2009). Brain oscillatory substrates of visual short-term memory capacity. *Current Biology*, *19*(21), 1846–1852.
- Siegel, M., Donner, T. H. & Engel, A. K. (2012). Spectral fingerprints of large-scale neuronal interactions. *Nature Reviews Neuroscience*, *13*(2), 121–134.
- Stefanics, G., Hangya, B., Hernádi, I., Winkler, I., Lakatos, P., & Ulbert, I. (2010). Phase entrainment of human delta oscillations can mediate the effects of expectation on reaction speed. *The Journal of Neuroscience*, *30*(41), 13578–13585.
- Telenczuk, B., Nikulin, V. V. & Curio, G. (2010). Role of neuronal synchrony in the generation of evoked EEG/MEG responses. *Journal of Neurophysiology*, *104*(6), 3557–3567.
- van Diepen, R. M., Foxe, J. J., & Mazaheri, A. (2019). The functional role of alpha-band activity in attentional processing: The current zeitgeist and future outlook. *Current Opinion in Psychology*, *29*, 229–238.
- van Diepen, R. M. & Mazaheri, A. (2018). The caveats of observing inter-trial phase-coherence in cognitive neuroscience. *Scientific Reports*, *8*(1), 2990.
- van Dijk, H., Schoffelen, J. M., Oostenveld, R., & Jensen, O. (2008). Prestimulus oscillatory activity in the alpha band predicts visual discrimination ability. *The Journal of Neuroscience*, *28*(8), 1816–1823.
- van Dijk, H., van der Werf, J., Mazaheri, A., Medendorp, W. P., & Jensen, O. (2010). Modulations in oscillatory activity with amplitude asymmetry can produce cognitively relevant eventrelated responses. *Proceedings of the National Academy of Sciences of the United States of America*, *107*(2), 900–905.
- Vogel, E. K., McCollough, A. W., & Machizawa, M. G. (2005). Neural measures reveal individual differences in controlling access to working memory. *Nature*, *438*(7067), 500–503.
- Yeung, N., Bogacz, R., Holroyd, C. B., & Cohen, J. D. (2004). Detection of synchronized oscillations in the electroencephalogram: An evaluation of methods. *Psychophysiology*, *41*(6), 822–832.
# [CHAPTER 7](#page-5-9)
# [FREQUENCY ANALYSIS OF](#page-5-9) [THE MONKEY NEO CORTICAL](#page-5-9) [LOCAL FIELD POTENTIAL](#page-5-9)
STEVEN L. BRESSLER
### **7.1 Introduction**
The neocortex of the macaque monkey is very similar to that of the human in its architectonics. The six neocortical laminae show similar variation with region in the monkey and human. In fact, it appears that all mammalian species share a common microstructure, which makes distinguishing neuroanatomical slices from different mammalian species under the microscope nearly impossible. What appears to be more different between the macaque monkey and human neocortices is at the macroscopic level. Overall, the number of neocortical areas is larger in the human brain, and the between-area connectivity is more complex. However, the macroscopic structure of the two species is highly similar in certain systems, for example, the visual system.
The similarity between the human and macaque monkey neocortex was first recognized for the visual system, where neocortical oscillations are a prominent product of the visual architecture of both humans and monkeys. Visual neocortical local field potentials (LFPs) show oscillations in both low-frequency (delta, theta, and alpha) and high-frequency (beta and gamma) bands. Many studies report the importance of the neocortical LFP oscillations in the boundary frequency region between the low beta (13–20 Hz) and alpha (8–12 Hz) frequency bands for top-down neocortical processing in vision (Liang et al., 2002; Bressler et al., 1993; Bressler et al., 2007; Engel & Fries, 2010; Bressler & Richter, 2015; Bastos et al., 2015; Richter et al.,2018), and in the theta (4–7 Hz) and gamma (above >30 Hz) bands for bottom-up visual processing (Markov et al., 2013; Bastos et al., 2015; Michalareas et al., 2016).
A great deal of research has also involved oscillatory activity in the prefrontal cortex of the macaque monkey, which has important analogies to the human prefrontal cortex, 132 STEVEN L. BRESSLER
which is the most developed of all the mammalian species and is therefore unique. The macaque monkey prefrontal cortex is clearly different from that of the human, but it shares many of the same features. As working memory is an essential component of different cognitive functions requiring the prefrontal cortex in both macaque monkeys and humans (Miller et al., 2018), studies of working memory in the macaque monkey prefrontal cortex are essential for understanding human working memory. Monkey studies first demonstrated a role for prefrontal neocortical oscillatory activity in working memory (Siegel et al.,2009), and these provided the theory that neocortical oscillations are important for working memory processes in the beta-alpha and gamma bands (Pesaran et al., 2002; Salazar et al., 2012; Antzoulatos & Miller, 2016). This speculation has now been verified (discussed later; see also Lundqvist et al.,2016, 2018; Miller et al., 2018).
The study of working memory oscillations in the monkey prefrontal cortex gives impetus to the investigation of prefrontal neocortical oscillations in human working memory (D'Esposito et al., 1995), and recent human studies demonstrate the importance of prefrontal oscillatory activity in human working memory (Jensen et al., 2007; Alekseichuk et al., 2016). Research by Miller and colleagues (2018) involving macaque monkeys verifies that working memory oscillations exist in the theta, alpha-beta, and gamma frequency bands. These oscillations are best studied in monkeys, which demonstrate excellent working memory capability, have associated oscillations that can be studied invasively, and which have a prefrontal neuroanatomy that is similar to humans. Questions about working memory and high-frequency (beta and gamma) oscillations tend to be addressed using monkeys due to the relatively low signal-to-noise ratio at higher frequencies in the human electroencephalogram (EEG) (Crone et al., 2006). The purpose of this report is to present evidence on neocortical oscillations from the macaque monkey engaged in cognitive functions that rely on working memory.
## **7.2 Dendrites, Oscillations, and Cognition**
Transmembrane ionic currents contribute to the extracellular field. Synaptic activity is often the most important physiological source of extracellular current flow. The dendrites and soma of a neuron are treelike and have an electrically conducting interior surrounded by a permeable but insulating membrane. Transmembrane current flows into the dendrites of neocortical neurons at excitatory synapses due to electromotive forces created by neurotransmitter molecules acting on postsynaptic receptor molecules, or out of the synaptic regions at inhibitory synapses. In either case, current flows down the length of the dendritic shaft, across the dendritic membrane, and completes a current loop through the extracellular space. The extracellular current loops give rise to extracellular potential differences that are detected as the LFP (Freeman,132 STEVEN L. BRESSLER
which is the most developed of all the mammalian species and is therefore unique. The macaque monkey prefrontal cortex is clearly different from that of the human, but it shares many of the same features. As working memory is an essential component of different cognitive functions requiring the prefrontal cortex in both macaque monkeys and humans (Miller et al., 2018), studies of working memory in the macaque monkey prefrontal cortex are essential for understanding human working memory. Monkey studies first demonstrated a role for prefrontal neocortical oscillatory activity in working memory (Siegel et al.,2009), and these provided the theory that neocortical oscillations are important for working memory processes in the beta-alpha and gamma bands (Pesaran et al., 2002; Salazar et al., 2012; Antzoulatos & Miller, 2016). This speculation has now been verified (discussed later; see also Lundqvist et al.,2016, 2018; Miller et al., 2018).
The study of working memory oscillations in the monkey prefrontal cortex gives impetus to the investigation of prefrontal neocortical oscillations in human working memory (D'Esposito et al., 1995), and recent human studies demonstrate the importance of prefrontal oscillatory activity in human working memory (Jensen et al., 2007; Alekseichuk et al., 2016). Research by Miller and colleagues (2018) involving macaque monkeys verifies that working memory oscillations exist in the theta, alpha-beta, and gamma frequency bands. These oscillations are best studied in monkeys, which demonstrate excellent working memory capability, have associated oscillations that can be studied invasively, and which have a prefrontal neuroanatomy that is similar to humans. Questions about working memory and high-frequency (beta and gamma) oscillations tend to be addressed using monkeys due to the relatively low signal-to-noise ratio at higher frequencies in the human electroencephalogram (EEG) (Crone et al., 2006). The purpose of this report is to present evidence on neocortical oscillations from the macaque monkey engaged in cognitive functions that rely on working memory.
# **7.2 Dendrites, Oscillations, and Cognition**
Transmembrane ionic currents contribute to the extracellular field. Synaptic activity is often the most important physiological source of extracellular current flow. The dendrites and soma of a neuron are treelike and have an electrically conducting interior surrounded by a permeable but insulating membrane. Transmembrane current flows into the dendrites of neocortical neurons at excitatory synapses due to electromotive forces created by neurotransmitter molecules acting on postsynaptic receptor molecules, or out of the synaptic regions at inhibitory synapses. In either case, current flows down the length of the dendritic shaft, across the dendritic membrane, and completes a current loop through the extracellular space. The extracellular current loops give rise to extracellular potential differences that are detected as the LFP (Freeman, FREQUENCY ANALYSIS OF THE MONKEY 133
1975; Buzsaki et al., 2012). The MEG is thought to arise from those same currents passing through the dendritic shafts of the same neurons (Murakami & Okada, 2006). Oscillatory activity is a prominent feature of both electric and magnetic signals, higher frequency oscillations likely reflecting interactions of excitatory and inhibitory neurons (Kopell, 2000).
There is growing recognition that the dendrites of neocortical neurons are thus essential for the genesis of neocortical oscillations, and there is speculation that the dynamics of cognitive processing, including working memory (Voytek & Knight, 2015), depends on oscillations. However, the recording and characterization of dendritic activity is problematic. It is usually not possible to record from single dendrites of neurons in the brain due to their thinness, or from the dendritic trees of single neurons due to the lack of extracellular potentials from single-neuron dendrites. Also, neither the singleneuron dendritic branch response nor the single-neuron dendritic tree response can be extracted from the compound dendritic response. For these reasons, much of neurophysiology has focused on the action potential (spike) as the essential neuronal signal. This focus is not because of the neuron doctrine, which, holding only that the neuron is the central signaling cell in the nervous system, is neutral with respect to the parts of the neuron that carry out particular aspects of that signaling.
Dendritic activity, and hence oscillatory activity, is typically recorded at the population level—from groups of neurons rather than from single neurons. In most neurons, the resultant sum of synaptic actions from an entire dendritic tree, contributed to by thousands of synaptic potentials, is delivered to the initial segment of the axon, where it causes the resultant axonal membrane potential to be graded in intensity. The membrane potential of the initial segment has a low threshold for generating a spike because voltage-sensitive Na + membrane channels are concentrated there. The recorded axonal membrane potential may be supra-threshold if the membrane potential is above the threshold, in which case spike trains are generated and travel down the axon, or subthreshold, in which case the axon may be affected but no spike trains are generated. The spike trains may contribute to the neuronal synchronization underlying the LFP (Murthy & Fetz, 1996).
The EEG, electrocorticogram (ECoG), intracranial EEG (iEEG), magnetoencephalogram (MEG), and LFP signals all are generated by the dendritic activity of neuronal populations, and all display oscillations. Except for the MEG, which is magnetic, all these signals are electric and are recorded with respect to a reference potential. The EEG and MEG are usually recorded from outside the cranium, whereas the ECoG, iEEG, and LFP are recorded from inside the cranium. The ECoG is recorded from outside the cortical tissue, whereas the iEEG and LFP are recorded from inside the cortex. The iEEG is recorded from macroscopic electrodes and the LFP is usually recorded with indwelling microelectrodes. The LFP recording may be monopolar, in which case a single microelectrode records the LFP, or it may be bipolar, in which case the LFP is the difference in potential between two nearby microelectrodes. In fact, the LFP is often recorded from the same microelectrodes used to record neuronal spikes, 134 STEVEN L. BRESSLER
and at the same time (Perelman & Ginosar, 2007; Salazar et al., 2012). However, the LFP typically shows oscillations whereas they are usually not obvious in spike activity.
Since these signal types all reveal oscillatory activity, which is considered by many to be essential for cognition in the brain (Voytek & Knight, 2015), and are typically present when humans perform cognitive tasks, the dendritic activity of neurons in the brain should not be overlooked in the search for neural correlates of cognition, even though it cannot currently be studied in the single neuron. Oscillations in the summed dendritic activity of neuronal populations are strongly related to cognitive function in the neocortex (Donner & Siegel, 2011).
# **7.3 Phase Coupling and Causality in Sensorimotor Systems**
The somatosensory-motor system provides a useful example of neocortical coordination during a cognitive task performed by the macaque monkey. LFP oscillations recorded from somatosensory and motor sites in the macaque monkey neocortex are phase coupled in the beta frequency band during the time in the task that a selfgenerated hand press cues the monkey by somatosensation that a visual stimulus (0 msec) is soon to appear on a visual display screen. The stimulus is subsequently perceptually discriminated as part of a visual pattern discrimination task requiring hand musculature control (Brovelli et al., 2004). LFPs from specific site pairs in primary and secondary somatosensory cortices, and primary and secondary motor cortex, become beta-phase-coupled (phase synchronized) when the hand press cue is active (Figure 7.1). The presence of beta oscillations in sensorimotor cortex is consistent with the theory that beta oscillations signal maintenance of the current sensorimotor state (Engel & Fries, 2010) since sensorimotor coordination (LFP phase coupling) is likely present throughout this time. The pattern of somatosensory-motor site-pair coupling is consistent with execution of the hand press cue: somatosensory input is fed to the primary somatosensory cortex and motor output is transmitted from the primary motor cortex to the motor spinal cord to execute the hand press. In addition to phase coupling, conditional spectral Wiener–Granger (WG) causality (Ding et al., 2006) was also measured on the same set of sensorimotor LFP recordings. The resulting pattern of sensorimotor neocortical site-pair neural causality also supports a sensorimotor feedback loop for execution of the hand press cue, with influences that are directed to the primary somatosensory cortex from somatosensory inputs, and from there to the primary motor cortex, with feedback loops between primary and secondary somatosensory cortices, and between primary and secondary motor cortices, signaling modulatory influences (Figure 7.1).
The fact that the observed oscillations are in the beta frequency band suggests that sensorimotor neocortical neurons are coordinated in anticipation of making a
FREQUENCY ANALYSIS OF THE MONKEY 135

**Figure 7.1** Prestimulus beta-frequency coherence and (conditional spectral Wiener-) Granger causality graphs derived from the sensorimotor cortices of two monkeys (M1, left hemisphere; M2, right hemisphere). A self-generated hand press cues the monkey that a visual stimulus is soon to appear on a visual display screen. The stimulus is subsequently perceptually discriminated as part of a visual pattern discrimination task (Brovelli et al., 2004). In each case, the pattern of synchronization (coherence) and Granger causality of beta-band oscillations from primary and secondary somatosensory and motor cortices is consistent with execution of the hand press cue: somatosensory input is fed to the primary somatosensory cortex and motor output is transmitted from the primary motor cortex to the motor spinal cord to execute the hand press.
sensorimotor decision in similar manner to the coordination of motor neocortical neurons during steady muscle contractions and steady holding periods following phasic movements as reported by numerous literature studies (e.g., Engel & Fries, 2010). Thus, when the monkey makes a hand press on the lever, sensorimotor neocortical neurons are coordinated in anticipation of the monkey making the subsequent sensorimotor decision. The observation of conditional spectral WG causality from neurons at one sensorimotor neocortical site to those at another site appears to indicate more than the observation of phase coupling alone by suggesting that sensorimotor neocortical neurons causally influence each other as part of that decision. Finally, the reported results are consistent with accumulating evidence that oscillations in the beta frequency band have a distinct physiological role and that they provide an effective means of controlling spike timing, thereby coordinating information transfer across brain regions and supporting spike-timing dependent plasticity (Engel & Fries, 2010).
136 STEVEN L. BRESSLER
# **7.4 Phase Coupling and Causality in Visual Neocortex**
LFPs, simultaneously recorded from the striate and extrastriate (V4—visual area 4 and TEO—temporal-occipital area) visual cortices prior to appearance of the visual stimulus in the same visual pattern discrimination task (Bressler & Richter, 2015), also show oscillatory activity in the beta frequency range. The same phase-coupling and neural causality metrics have been computed from the visual LFPs as from somatosensory-motor LFPs. The main finding is that extrastriate–striate site pairs are beta-frequency phase coupled and carried by strong top-down (extrastriate-to-striate) beta influences, in anticipation of visual processing (Figures 7.2 and 7.3). Furthermore, behavioral context is conveyed to primary visual cortex prior to appearance of the visual stimulus (Richter et al., 2018). Thus, information about the visual stimulus appears in the visual cortex

**Figure 7.2** Prestimulus beta-frequency power, coherence, and (conditional spectral Wiener-Granger causality spectra of V1/V2 and V4/TEO LFPs. (A) Average striate power spectrum over sites (black line ± s.e.m.), and the residual power spectrum after 1/f removal (red line ± s.e.m.) for V1 sites. (B) Average extrastriate power spectrum over sites and monkeys (black line ± s.e.m.), and the residual power spectrum after 1/f removal (red line ± s.e.m.) for the V4/TEO sites. (C) Average coherence spectrum over V1/V2-extrastriate site pairs ± s.e.m. for V1/V2-extrastriate pairs. (D) Average top-down (red line ± s.e.m.), and bottom-up (blue line ± s.e.m.) GC spectra for V1-extrastriate pairs. Shaded grey rectangular region denotes the frequencies (8–23 Hz) where top-down and bottom-up sGC were significantly different (p<0.001).
FREQUENCY ANALYSIS OF THE MONKEY 137

**Figure 7.3** Prestimulus beta-frequency coherence and top-down (conditional spectral Wiener- )Granger causality maps. Top: Maps of the recording sites for M1 and M2. V1/V2 electrode locations are marked by yellow circles, and extrastriate (V4 and TEO) locations by gray circles. Middle: enlarged maps of visual cortex showing top-down sGC at 16 Hz as arrows for V1/V2 extrastriate pairs. Bottom: corresponding maps of coherence for the same site pairs. Thickness of the top-down sGC arrows and coherence bars is proportional to the magnitude of sGC or coherence at 16 Hz.
before the actual onset of the visual stimulus. This result validates previous proposals that top-down visual processing depends on interareal synchronization in visual neocortex (von Stein et al., 2000), and suggests that it acts to "prime" visual cortex to prepare it for receiving the visual stimulus.
The same basic methodology, namely conditional spectral WG causality analysis, has subsequently been applied to visual neocortical LFPs in macaque monkeys performing a visuospatial attention task (Bastos et al., 2015). In the visual system, neocortical areas are seen to interact in both bottom-up and top-down directions, with bottom-up gamma-band influences conveying sensory signals, and top-down beta-band influences modulating those bottom-up influences according to behavioral context. In the macaque monkey visual neocortex, bottom-up influences are carried by theta-band (~4 Hz) and gamma-band (~60–80 Hz) synchronization, and top-down influences by beta-band (~14–18 Hz) synchronization (Bastos et al. 2015). Furthermore, neocortical hierarchies (Felleman & Van Essen, 1991; Hilgetag et al., 1996) created based on 138 STEVEN L. BRESSLER
asymmetries in these directional influences are similar to those based on asymmetries in neuroanatomical connections (Markov et al., 2014).
Effective interareal interaction in the visual system depends on local (within-area) synchronization of oscillations that are layer specific. Supragranular layers show local gamma-band synchronization, whereas infragranular layers show local alpha-/ beta-band synchronization (Buffalo et al., 2011; Xing et al., 2012; Roberts et al., 2013). Since supragranular layers primarily send bottom-up projections, and infragranular layers primarily send top-down projections, it is proposed that interareal synchronization in the gamma band mediates bottom-up influences and that the beta band mediates top-down influences (Wang, 2010; Bastos et al., 2012; van Kerkoerle et al., 2014).
Metrics of the bottom-up or top-down character of interareal connections have been used to create neocortical hierarchies. A functional metric of directed influence is computed as the *d*irected influence *a*symmetry *i*ndex (DAI), based on the conditional spectral WG causality in bottom-up and top-down directions. A neuroanatomical metric of directional influence is computed as the proportion of supragranular labeled neurons to the sum of supragranular and infragranular labeled neurons (SLN). The DAI and SLN metrics quantify the degree to which an interareal projection is top-down or bottom-up. These hierarchies are generally similar whether created from conditional spectral WG causality or from neuroanatomical metrics. The functional hierarchies further demonstrate that bottom-up influences utilize theta and gamma bands, whereas top-down influences utilize the beta band. If directional influences represent interareal communication, and, as has been speculated (Bastos et al., 2015), increasing oscillation frequency entails increasing communication throughput, then gamma-band communication might be expected for bottom-up influences, since they are expected to require higher-throughput communication.
The finding of top-down beta influences in the visual system (Bastos et al., 2015) is consistent with Richter and colleagues' (2018) results that top-down beta signaling conveys behavioral context to the visual cortex, and with the general conclusion that beta-band synchrony signals the "status-quo" in neocortex (Engel & Fries, 2010). In fact, a distributed network of phase-coupled beta-band oscillations might easily signal predicted sensory and motor events (Bastos et al., 2012; Bressler & Richter, 2015).
# **7.5 Oscillations in Prefrontal Neocortex**
Monkey LFP oscillations have been reported during working memory in the theta, alpha, beta, and gamma bands. The gamma band is associated with sensory information, FREQUENCY ANALYSIS OF THE MONKEY 139
and gamma-band power correlates with the number of objects held in working memory, whereas the beta band is associated with top-down information, and betaband synchrony correlates with task rules (Liang et al., 2002; Miller et al., 2018; Richter et al., 2018). Gamma bursting is anti-correlated with alpha-beta bursting (Lundqvist et al., 2016).
Information in prefrontal neuronal spiking has been linked to brief bursts in the gamma band in monkeys performing a working memory task (Lundqvist et al., 2016). Prefrontal laminar LFP data has been obtained from monkeys using prefrontal laminar probes (Bastos et al., 2018). Gamma-band activity is strongest in the superficial layers, and beta and alpha LFP power is strongest in the deep layers. In keeping with previous studies (Lundqvist et al., 2016), gamma-band bursting is most informative about working memory in the superficial layers.
Gamma-band bursts, varying in time and frequency, were reported to accompany both the encoding and re-activation of sensory information (Bastos et al., 2015). The conclusion is that gamma bursts could gate access to, and prevent sensory interference with, working memory, since only the neuronal activity that was associated with working memory encoding and decoding was correlated with gamma-band burst rate changes. Bursts in the beta band were also brief and variable, but they reflected a "default state" that was interrupted by encoding and decoding.
# **7.6 Phase Coupling and Causality in the Fronto-Parietal Network**
The prefrontal cortex is not the only region of neocortex involved in working memory. To test the involvement of posterior parietal cortex in working memory, LFPs were recorded from distributed sites in the prefrontal cortex and in the posterior parietal cortex of macaque monkeys performing a working memory delayedmatch-to-sample visual identity task (Salazar et al., 2012). Phase coupling between prefrontal and posterior parietal cortices, examined by computing spectral coherence between prefrontal-posterior parietal LFP pairs, was found in the beta frequency band. Analysis of prefrontal-posterior parietal interactions in working memory by conditional spectral WG causality applied to the delay period of the delayed matchto-sample visual identity task showed that the beta frequency band was dominant. Causal influences in the beta band were roughly balanced between the two directions, that is, beta causal influences in the prefrontal-to-posterior parietal and posterior parietal-to-prefrontal directions were roughly the same (slightly greater from posterior parietal cortex to prefrontal cortex). This finding indicates that prefrontal and posterior parietal cortices are roughly in balance during working memory task performance.
140 STEVEN L. BRESSLER
## **7.7 Conclusions**
This chapter focused on neocortical oscillations in the macaque monkey related to cognitive processes in visual pattern discrimination, visuospatial attention, and visual working memory tasks. In visual processing, beta-frequency oscillatory influences predominate in the top-down direction prior to arrival of the visual stimulus, suggesting that beta-frequency oscillations convey task rule-related information from higher to lower areas of visual neocortex for visual processing during vision.
In visual working memory, the prefrontal cortex and posterior parietal cortex in both monkeys and humans are expected to be linked together as parts of the fronto-parietal network (Salazar et al., 2012; Alekseichuk et al., 2016). Beta-frequency oscillations are found to link posterior parietal and prefrontal cortex, with slightly greater causal influence from the posterior parietal cortex to the prefrontal cortex. Oscillations in the gamma and theta frequency bands are also prominent in neocortex in working memory. The gamma band is associated with sensory information in monkey working memory. The theta band is associated with human working memory (Raghavachari et al., 2001). Potential topics for future investigation are the presence of gamma oscillations in the human prefrontal cortex during working memory (Howard et al., 2003), and their relation to theta oscillations (Jokisch & Jensen, 2007).
Oscillations in different frequency bands are exhibited in the monkey neocortex in relation to cognitive function. These oscillations are similar to those in humans, and therefore should be considered when trying to understand the role of oscillations in human cognition. Prominent among the frequency bands at play in cognition involving visual and prefrontal systems are theta, alpha-beta, and gamma. These bands are foremost among those found in visual cortex, prefrontal cortex, and posterior parietal cortex in relation to visual pattern discrimination and visual working memory.
#### **References**
Alekseichuk, I., Turi, Z., Amador de Lara, G., Antal, A., & Paulus, W. (2016). Spatial working memory in humans depends on theta and high gamma synchronization in the prefrontal cortex. *Current Biology, 26*, 1513–1521.
Antzoulatos, E. & Miller, E. (2016). Synchronous beta rhythms of frontoparietal networks support only behaviorally relevant representations. *eLife,5*, e17822.doi: 10.7554/eLife.17822
Bastos, A., Litvak, V., Moran, R., Bosman, C., Fries, P., & Friston, K. (2015). A DCM study of spectral asymmetries in feedforward and feedback connections between visual areas V1 and V4 in the monkey. *Neuroimage*, *108*, 460–475.
Bastos, A., Loonis, R., Kornblith, S., Lundqvist, M., & Miller, E. (2018). Laminar recordings in frontal cortex suggest distinct layers for maintenance and control of working memory. *Proceedings of the National Academy of Sciences of the United States of America,115*, 1117–1122.
Bastos, A., Usrey, W., Adams, R., Mangun, G., Fries, P., & Friston, K. (2012). Canonical microcircuits for predictive coding. *Neuron, 76*, 695–711.
FREQUENCY ANALYSIS OF THE MONKEY 141
- Bressler, S., Coppola, R., & Nakamura, R. (1993). Episodic multiregional cortical coherence at multiple frequencies during visual task performance. *Nature,366*, 153–156.
- Bressler, S., Richter, C., Chen, Y., & Ding, M. (2007). Cortical functional network organization from autoregressive modeling of local field potential oscillations. *Statistics in Medicine, 26*, 3875–3885.
- Bressler, S. & Richter, C. (2015). Interareal oscillatory synchronization in top-down neocortical processing. *Current Opinion in Neurobiology,31C*, 62–66.
- Brovelli, A., Ding, M., Ledberg, A., Chen, Y., Nakamura, R., & Bressler, S. (2004). Beta oscillations in a large-scale cortical network: Directional influences revealed by Granger causality. *Proceedings of the National Academy of Sciences of the United States of America, 101*, 9849–9854.
- Buffalo, E., Fries, P., Landman, R., Buschman, T., & Desimone, R. (2011). Laminar differences in gamma and alpha coherence in the ventral stream. *Proceedings of the National Academy of Sciences of the United States of America,108*, 11262–11267.
- Buzsaki, G., Anastassiou, C., & Koch, C. (2012). The origin of extracellular fields and currents— EEG, ECoG, LFP and spikes. *Nature Reviews Neuroscience, 13*, 407–420.
- Crone, N., Sinai, A., & Korzeniewska, A. (2006). High-frequency gamma oscillations and human brain mapping with electrocorticography. *Progress in Brain Research, 159*, 275–295.
- D'Esposito M, Detre J, Alsop D, Shin R, Atlas S, Grossman M (1995) The neural basis of the central executive system in working memory. *Nature,378*, 279–281.
- Ding, M., Chen, Y., & Bressler, S. (2006). Granger causality: Basic theory and application to neuroscience. In B. Schelter, M. Winterhalder, & J. Timmer (Eds.), *Handbook of time series analysis: Recent theoretical developments and applications*, (pp. 437–460). Wiley.
- Donner, T. & Siegal, M. (2011). A framework for local cortical oscillation patterns. *Trends in Cognitive Science, 15*, 191–199.
- Engel, A. & Fries, P. (2010). Beta-band oscillations signaling the status quo? *Current Opinion in Neurobiology, 20*, 156–165.
- Felleman, D. & Van Essen, D. (1991). Distributed hierarchical processing in the primate cerebral cortex. *Cerebral Cortex, 1*, 1–47.
- Freeman, W. (1975). *Mass action in the nervous system*. Academic.
- Hilgetag, C., O'Neill, M., & Young, M. (1996). Indeterminate organization of the visual system. *Science, 271*, 776–777.
- Howard, M., Rizzuto, D., Caplan, J., Madsen, J., Lisman, J., Aschenbrenner-Scheibe, R., Schulze-Bonhage, A., & Kahana, M. (2003). Gamma oscillations correlate with working memory load in humans. *Cerebral Cortex, 13*, 1369–1374.
- Jensen, O., Kaiser, J., & Lachaux, J. (2007). Human gamma-frequency oscillations associated with attention and memory. *Trends in Neuroscience,30*, 317–324.
- Jokisch, D. & Jensen, O. (2007). Modulation of gamma and alpha activity during a working memory task engaging the dorsal or ventral stream. *Journal of Neuroscience, 27*, 3244–3251.
- Kopell, N. (2000). We got rhythm: Dynamical systems of the nervous system. *Notices of the American Mathematical Society, 47*, 6–16.
- Liang, H., Bressler, S., Ding, M., Truccolo, W., & Nakamura, R. (2002). Synchronized activity in prefrontal cortex during anticipation of visuomotor processing. *Neuroreports, 13*, 2011–2015.
- Lundqvist, M., Rose, J., Herman, P., Brincat, S., Buschman, T., & Miller, E. (2016). Gamma and beta bursts underlie working memory. *Neuron, 90*, 152–164.
- Lundqvist, M., Herman, P., Warden, M., Brincat, S., & Miller, E. (2018). Gamma and beta bursts during working memory readout suggest roles in its volitional control. *Nature Communications, 9*, 394.
142 STEVEN L. BRESSLER
- Markov, N., Ercsey-Ravasz, M., Van Essen, D., Knoblauch, K., Toroczkai, Z., & Kennedy, H. (2013). Cortical high-density counterstream architectures. *Science,342*, 1238406.
- Markov, N., Vezoli, J., Chameau, P., Falchier, A., Quilodran, R., Huissod, C., Lamy, C., Misery, P., . . . Kennedy, H. (2014). Anatomy of hierarchy: Feedforward and feedback pathways in macaque visual cortex. *Journal of Comparative Neurology,522*, 225–229.
- Michalareas, G., Vezoli, J., Van Pelt, S., Schoffelen, J-M., Kennedy, H., & Fries, P. (2016). Alphabeta and gamma rhythms subserve feedback and feedforward influences among human visual cortical areas. *Neuron, 46*, 60528.
- Miller, E., Lundqvist, M., & Bastos, A. (2018). Working memory 2.0. *Neuron, 100*, 463–475.
- Murakami, S. & Okada, Y. (2006). Contributions of principal neocortical neurons to magnetoencephalography and electroencephalography signals. *Journal of Physiology, 575*, 925–936.
- Murthy, V. & Fetz, E. (1996). Synchronization of neurons during local field potential oscillations in sensorimotor cortex of awake monkeys. *Journal of Neurophysiology, 76*, 3968–3982.
- Perelman, Y. & Ginosar, R. (2007). An integrated system for multichannel recording with spike/ LFP separation, integrated A/D conversion, and threshold detection. *IEEE Transactions on Biomedical Engineering,54*, 130–137.
- Pesaran, B., Pezaris, J., Sahani, M., Mitra, P., & Anderson, R. (2002). Temporal structure in neuronal activity during working memory in macaque parietal cortex. *Nature Neuroscience,5*, 805–81.
- Raghavachari, S., Kahana, M., Rizzuto, D., Caplan, J., Kirschen, M., Bourgeois, B., Madsen, J., & Lisman, J. (2001). Gating of human theta oscillations by a working memory task. *Journal of Neuroscience, 21*, 3175–3183.
- Richter, C., Copolla, R., & Bressler, S. (2018). Top-down beta oscillatory signaling conveys behavioral context in early visual cortex. *Scientific Reports, 8*, 6991.
- Roberts, M., Lowet, E., Brunet, N., Ter Wal, M., Tiesinga, P., Fries, P., & De Weerd, P. (2013). Robust gamma coherence between macaque V1 and V2 by dynamic frequency matching. *Neuron, 78*, 523–536
- Salazar, R., Dotson, N., Bressler, S., & Gray, C. (2012). Content-specific fronto-parietal synchronization during visual working memory. *Science,338*, 1097–1100
- Siegel, M., Warden, M., & Miller, E. (2009). Phase-dependent neuronal coding of objects in short-term memory. *Proceedings of the National Academy of Sciences of the United States of America, 106*, 21341–21346
- Van Kerkoerle, T., Self, M., Dagnino, B., Gariel-Mathis, M-A., Poort, J., van der Togt, C., & Roelfsema, P. (2014). Alpha and gamma oscillations characterize feedback and feedforward processing in monkey visual cortex. *Proceedings of the National Academy of Sciences of the United States of America, 111*, 14332–14341.
- von Stein, A., Chiang, C., & Konig, P. (2000). Top-down processing mediated by interareal synchronization. *Proceedings of the National Academy of Sciences of the United States of America, 97*, 14748–14753.
- Voytek, B. & Knight, R. (2015). Dynamic network communication as a unifying neural basis for cognition, development, aging, and disease. *Biol Psych 77*, 1089–1097.
- Wang, X-J. (2010). Neurophysiological and computational principles of cortical rhythms in cognition. *Physiological Reviews, 90*, 1195–1268.
- Xing, B., Guo, J., Meng, X., Wei, S-G., & Li, S-B. (2012). The dopamine D1 but not D3 receptor plays a fundamental role in spatial working memory and BDNF expression in prefrontal cortex of mice. *Behavioral Brain Research, 235*, 36–41.
# Part II
## [CHAPTER 8](#page-6-0)
# [GAMMA ACTIVIT Y IN](#page-6-0) [SENSORY AND CO GNITIVE](#page-6-0) [PROCESSING](#page-6-0)
DANIEL STRÜBER AND CHRISTOPH S. HERRMANN
# **8.1 Introduction and history of research on gamma oscillations**
When the German psychiatrist Hans Berger reported his discovery of the human EEG in 1929, he described two types of waves with the larger ones oscillating at 10–11 Hz and the smaller ones at 20–30 Hz (Berger, 1929)—the well-known alpha- and beta-waves, respectively. However, in view of the results from the first Fourier analysis carried out on the human EEG by his physicist co-worker Dietsch (1932), Berger had to acknowledge that his beta-waves contained a lot more components than originally thought with frequencies up to 125 Hz (Berger, 1934;1936). By comparing spontaneous EEG recordings with recordings during mental calculation, Berger (1937) observed effects predominantly in the 40–90 Hz range which led him to conclude that beta-waves of this specific (high-)frequency band "are the physical effects that accompany mental processes". One year later, the term "gamma waves" was proposed for higher frequencies at 35–45 Hz, that is, beyond the traditional beta-band (Jasper & Andrews, 1938). However, this firsttime labeling went mostly unnoticed at that time and "gamma" was later reintroduced by other authors (e.g., Başar & Özesmi, 1972; Bressler & Freeman, 1980). Instead of "gamma", the term "40-Hz oscillation" is also widely used.
The first experimental evidence for a possible role of gamma oscillations in early sensory processing in the mammalian brain was provided by Adrian (1942; 1950), who recorded oscillatory responses of the olfactory bulb of hedgehogs, cats, and rabbits to odorous substances. He obtained oscillatory responses in the 30–60 Hz frequency range which he termed "induced waves" to differentiate these events from "intrinsic 146 DANIEL STRÜBER and CHRISTOPH S. HERRMANN
waves", signaling spontaneous activity (Adrian, 1950). Inspired by Adrian's suggestion that neurons responding preferentially to certain odors might be spatially organized, Freeman collected multi-channel EEG recordings from the surface of the olfactory bulb of rabbits trained to respond to different odorants (Freeman & Skarda, 1985; Freeman, 1975). These analyses revealed odor-specific spatial amplitude patterns of transient gamma bursts at 40–80 Hz occurring between inhalation and response, reflecting a spatial code of Adrian's induced waves that seemed to underlie the discrimination of odors.
In addition to the pioneering studies of Freeman on the olfactory bulb of the rabbit, Başar and colleagues observed "gamma resonance" phenomena in the hippocampus and other structures of the cat brain in response to auditory stimulation (Başar et al., 1975; Başar et al., 1976; Başar & Özesmi, 1972), that is, an amplification of the gamma frequency component of the evoked potential in relation to the spontaneous gamma activity just before stimulation. Resonance phenomena have also been studied by recording the evoked potential in response to repetitive stimulation at different frequencies (so-called steady-state evoked potentials, Regan & Spekreijse, 1986). If the amplitude of the steadystate response peaks at a certain frequency, this component is interpreted as the resonance frequency of the underlying oscillator. For gamma oscillations in the human visual cortex, Regan (1968) first demonstrated a peak frequency of 45–55 Hz by using photic stimulation flickering between 5 and 60 Hz. Later on, Herrmann (2001) applied flickering light at frequencies from 1 to 100 Hz and found clear resonance phenomena in the gamma range. For the auditory modality, Galambos and colleagues (1981) reported a comparable phenomenon at 40 Hz in response to tone bursts at different rates, which the authors termed the auditory "40-Hz event-related potential".
Whereas most of the early studies on gamma activity were concerned with its role in sensory processing, the first attempts to relate gamma to more cognitive processes lacking a strict relation to stimulation were in the late 1970's and early 1980's. One prominent example is the work of Sheer (1984), who used 40 Hz EEG as a measure for changing states of focused arousal during cognitive tasks in humans (e.g., Spydell et al., 1979). Similarly in the cat neocortex, fronto-parietal gamma band coherence was shown to increase during states of expectancy and focused attention (Bouyer et al., 1981). These studies pioneered the current notion of a role for gamma oscillations in top-down attentional networks (Engel et al., 2001).
In the late 1980's, Gray & Singer (1989) revolutionized the research on gamma activity by observing synchronous gamma oscillations in spiking activity of the cat visual cortex in response to light stimuli. Gray and collaborators (1989) extended their initial finding of short-range gamma synchronization to spatially more segregated cells. They demonstrated that neurons from distant parts of the visual cortex oscillate synchronously if presented with a coherent stimulus like a single long bar (or two shorter bars moving in the same direction), but not in case of two independent stimuli like two bars moving in opposite directions. This finding was highly influential because it suggested that gamma synchrony could serve as a mechanism for binding together different features to form a coherent object (see, for reviews, Engel et al., 1997; Singer & Gray, 1995).
GAMMA ACTIVITY IN SENSORY AND COGNITIVE PROCESSING 147
Such binding-related synchronization of oscillatory gamma responses between neural assemblies has not only been observed in the visual cortex of the anaesthetized cats (Eckhorn et al., 1988; Engel et al., 1991; Gray et al., 1989), but also in awake monkeys (Frien et al., 1994; Kreiter & Singer, 1996). This work stimulated a wealth of human EEG studies on gamma oscillations and their possible role in visual feature-binding and object representation (see, for review, Tallon-Baudry & Bertrand, 1999). However, it soon turned out that gamma oscillations are not related to a single function like visual grouping but that they subserve a multiplicity of cognitive functions, including attention, learning, memory, and language processing, to name just a few (for reviews, see Herrmann et al., 2010; Jensen et al., 2007; Pulvermüller et al., 1997; Tallon-Baudry, 2009).
Given this large variety of cognitive gamma correlates, the question arose whether there might be a common fundamental process to which the many functions can be reduced to. In this context, it has been proposed that basic memory mechanisms could underlie functions like attention, object representation, and language (Herrmann et al., 2004). Going further by including "non-cognitive" functions of gamma oscillations recorded from subcortical areas of the mammalian brain and even from invertebrate ganglia, it has been argued that gamma oscillations represent a universal operator acting in concert with other oscillatory systems to control the integrative brain functions at all sensory and cognitive levels (Başar, 2013; Başar-Eroǧlu, Strüber, Schürmann et al. 1996).
However, Whitham and colleagues (2007) challenged research on EEG gamma activity by demonstrating that most of the EEG gamma activity disappeared from the spectrum as a result of total neuromuscular blockade. In the following year, Yuval-Greenberg and colleagues' (2008) work questioned the widely held assumption that scalp-recorded induced gamma activity is of cortical origin. They demonstrated that this type of gamma activity coincides with the occurrence of miniature eye movement. The possibility that large parts of the EEG gamma activity were artefactual rather than neural activity had presented a major challenge to the EEG gamma community, and it is likely that many earlier reports on the role of induced gamma activity are heavily contaminated by muscular activity. Nevertheless, this does not mean that all previous research is invalidated because there are several methodological issues that need to be considered when evaluating how severe specific data sets are affected. There is clear evidence in the literature that neural gamma activity can, and has been, detected by means of EEG (Schwartzman & Kranczioch, 2011). Since then, research aims to develop artefact removal techniques in order to regain confidence into the functional role of EEG gamma activity (see Sections 8.8, 8.9).
## **8.2 Types of gamma activity**
Gamma oscillations are part of the total EEG energy to a varying degree at any moment in time. Such spontaneous or ongoing activity occurs independently of any external 148 DANIEL STRÜBER and CHRISTOPH S. HERRMANN
stimulation and may signal alterations of internal states like arousal or alertness (Strüber et al., 2001). If gamma oscillations are related to the processing of external stimuli, a distinction is made between "evoked" and "induced" activity (Başar-Eroǧlu, Strüber, Schürmann, et al., 1996). Evoked gamma responses are strictly time- and phase-locked to stimulus onset, that is, each single trial occurs at the same latency with zero phase lag across trials, therefore summing up after averaging. Thus, evoked activity can be analyzed by transforming the averaged single-trials (i.e., the averaged evoked potential, ERP) into the frequency domain (see Figure 8.1, left panel). This type of gamma activity is typically observed within an early time window of ~50–150 ms following stimulation onset. In contrast, induced activity occurs later, following stimulation by at least 200–300 ms, and it cancels out almost completely if averaged due to its inter-trial variation of phase and latency. Therefore, to detect induced gamma oscillations, each single trial needs to be subjected to a wavelet transform, and then the resulting absolute power

**Figure 8.1** Analysis of evoked and induced gamma activity. Left: Averaging all single trials containing evoked and induced gamma oscillations yields the ERP. Transforming the ERP into the time-frequency domain (wavelet transform) leaves only the evoked gamma activity, because the induced gamma activity cancels out in the ERP due to phase jitter. Right: Averaging the absolute values of each single trial's wavelet transform yields both evoked and induced activity (i.e., the total activity). Thus, evoked activity is obtained with both types of analyses, whereas induced gamma activity appears only in the average of the single trial wavelet transforms.
Adapted from Herrmann et al., 2014.
NB: The latency jitter of the induced activity induces temporal smearing in the total activity. a.u., arbitrary units.
GAMMA ACTIVITY IN SENSORY AND COGNITIVE PROCESSING 149
values are averaged across trials without cancellation (see Figure 8.1, right panel). Note, however, that this average contains not only the induced but also the evoked activity and has, therefore, been termed "total activity" (Herrmann et al., 2014). Within this plot of total activity, all activity that is not also present in the evoked plot, can be referred to as induced activity. While Figure 8.1 depicts the differences between the different types of gamma activity in principle, Figure 8.2 represents real data from human experiments.
In traditional EEG research, the range of gamma frequencies is given as 30–80 Hz with evoked activity often oscillating nearby 40 Hz, whereas induced responses can also reach higher frequencies (Herrmann, Munk, et al., 2004). However, in the context of subdural electrocorticography (ECoG) in epilepsy patients, a broad range of very high gamma frequencies (around 80–200 Hz) was discovered unexpectedly and called "high gamma" to distinguish this broadband response from the traditional "low gamma" oscillations in narrower bands (for a review, see Crone et al., 2011). Although

**Figure 8.2** Time-frequency plots and topographies of evoked and induced gamma activity. White box: Evoked gamma activity for pattern reversal (A) and motion (B). Yellow box: Induced gamma activity for pattern reversal (A) and motion (B) within the plot of total activity. Red box: Steady-state visual evoked potential (SSVEP) in the motion condition as a response to the single images representing the motion of the gratings. The green line represent stimulus onset. C: Topographic maps of evoked (left) and induced (right) gamma activity during an object recognition task. a.u.: arbitrary units.
(A, B) Adapted from Naue et al., 2011; (C) Adapted from Busch, Herrmann, et al., 2006.
150 DANIEL STRÜBER and CHRISTOPH S. HERRMANN
this broadband activity often overlaps with the band-limited (low) gamma oscillations, it is possible that such broadband responses reflect mere increases of (non-oscillatory) gamma power and/or spiking activity rather than a true oscillation (Buzsáki & Wang, 2012; Ray & Maunsell, 2011), since the latter would be indicated as a clear peak in the power spectrum. There is a recent debate about how to assess and interpret high gamma activity in the absence of a spectral peak (Brunet et al., 2014; Hermes et al., 2015). Further research is needed to elucidate the distinction between "low and high" or "narrow- and broadband" gamma activity in terms of their neurophysiological underpinnings and functional roles. In this context, note that the observation of high gamma responses is not bound by its superior signal-to-noise ratio to invasive depth recordings and ECoG in patients, as gamma responses in the 90-250 Hz range have also been recorded from conventional scalp EEGs of healthy volunteers (Darvas et al., 2010; Lenz, Jeschke, et al., 2008).
## **8.3 Evoked gamma activity**
In light of the latency difference between evoked (~50–150 ms) and induced gamma activity (~200–300 ms), it has been suggested that evoked activity reflects an early processing stage at the level of primary visual cortices (Zaehle et al., 2009), whereas induced activities occur at later stages (Herrmann et al., 2010). Findings of evoked gamma activity modulated by low-level physical features of visual stimuli support this view (for the sake of brevity, we focus on the visual domain in the remainder of this chapter). However, there is a remarkable overlap between evoked and induced gamma activity in reflecting sensory vs. cognitive effects, as demonstrated in the sequel.
Regarding stimulus-driven effects, early evoked gamma activity has been observed to increase with stimulus size and with central as compared to peripheral stimulation (Busch et al., 2004). Also high visual contrast (Schadow et al., 2007) and low spatial frequencies (Fründ et al., 2007) of simple grating stimuli increased the power of evoked gamma activity. With regard to motion, evoked gamma power did not differ between stationary and moving gratings (Naue et al., 2011; Swettenham et al., 2009). However, inverting the black and white stripes of a stationary grating (pattern reversal) led to a threefold increase of the evoked gamma amplitude compared to stationary and moving gratings, probably due to related contrast effects (Naue et al., 2011, see Figure 8.2).
These exemplary findings not only indicate an early processing stage of evoked gamma responses but also implicate that finding evoked gamma activity requires a corresponding design of physical stimulus parameters. Relatedly, before a cognitive effect on evoked gamma activity can be inferred from two experimental conditions, care must be taken that physically identical stimuli were used. Otherwise, differences of the evoked gamma response cannot unequivocally be attributed to the cognitive process under study.
GAMMA ACTIVITY IN SENSORY AND COGNITIVE PROCESSING 151
Cognitive effects on the evoked gamma activity have been observed in visual discrimination tasks where participants had to attend to a target and to ignore distractor stimuli that were physically more or less similar to the target (Herrmann & Mecklinger, 2001; Herrmann et al., 1999). The results not only demonstrated a target-effect (i.e., higher evoked gamma activity to attended stimuli), but also a graded effect of similarity between target and distractor stimuli (i.e., the more features a distractor shared with the target the stronger was the evoked gamma activity). This led to the suggestion that each stimulus is compared to a short-term memory template of the target and that the degree of matching between stimulus and template determines the strength of the evoked gamma activity. Similarly for long-term memory (LTM), a match between line drawings of real-world objects and their well-consolidated memory representation evoked stronger gamma responses than the perception of unfamiliar (non-)objects without an LTM representation (Herrmann et al., 2004).
Modulations of evoked gamma activity have also been reported in the context of visual semantic memory (Oppermann et al., 2012). Simultaneously presented pairs of conceptually coherent scenes (e.g., mouse–cheese) evoked stronger gamma-band responses than semantically unrelated object pairs (e.g., camel–magnet). This effect occurred within a widespread network of bilateral occipital as well as right temporal and frontal regions in a time window between 70–130 ms after stimulus onset, indicating a role of early gamma activity for a rapid memory-based extraction of the gist of a scene.
Together, studies on early evoked gamma oscillations demonstrate not only their sensitivity to low-level stimulus features but also an influence of cognitive effects occurring as early as 50–150 ms after stimulus onset, thereby revealing an early interaction between bottom-up and top-down processes in the gamma band (Busch et al., 2006).
## **8.4 Induced (total) gamma activity**
Especially the induced type of gamma activity has been consistently related to higher cognitive processes (Kaiser & Lutzenberger, 2005), motivated by the initial findings in animals suggesting a possible role of induced synchronous neural discharges in bottom-up feature binding (see Section 8.1; Eckhorn et al., 1988; Gray et al., 1989). By using protocols very similar to these animal studies, their main finding of an increase in the strength of induced gamma synchrony during passive viewing of coherent moving bars could be replicated in the human scalp EEG (Lutzenberger et al., 1995; Müller et al., 1996). Increases of induced gamma activity have also been reported in response to coherent versus incoherent static stimuli during a visual discrimination task. In a classical study, presenting an illusory Kanizsa triangle, a real triangle, and a no-triangle stimulus with the black inducer disks rotated outwards, resulted in specific enhancements of the induced gamma activity for the coherent triangles (illusory and real) as compared to the no-triangle stimuli (Tallon-Baudry et al., 1996).
152 DANIEL STRÜBER and CHRISTOPH S. HERRMANN
In addition to these relatively low-level feature binding processes originating from visual cortices, induced gamma activity has been observed also in higher stages of perceptual processing. For instance, at occipito-temporal and frontal areas during rehearsal of an object representation in short-term memory (Tallon-Baudry et al., 1998), and at occipito-parietal areas during the top-down activation of internal object representations (Tallon-Baudry et al., 1997), as well as during selective spatial attention to moving stimuli (Gruber et al., 1999). Together, those findings are in line with the interpretation of induced gamma activity as a signature of both bottom-up and topdown related binding processes involved in object representation (Tallon-Baudry & Bertrand, 1999).
Consistent with this "representational hypothesis" of induced gamma activity are studies demonstrating augmented gamma power and phase coupling during retrieval from LTM for familiar objects compared to unfamiliar ones (e.g., Busch et al., 2006; Gruber et al., 2006). Furthermore, in a recognition memory task, Gruber and colleagues (2004) showed that induced gamma activity during the encoding phase was higher for subsequently recognized words as compared to forgotten words.
Summerfield and Mangels (2006) describe similar enhancements of induced gamma activity during successful encoding, although they compared later memory performance between predictable items that were encoded under top-down attentional control and unpredictable items to which attention could not be oriented in a top-down manner during encoding. Enhanced gamma activity over frontal regions predicted successful memory formation for the predictable items only, indicating a role of frontal gamma activity in attentional top-down mechanisms facilitating memory formation (Summerfield & Mangels, 2006).
Interestingly, a frontal gamma-band enhancement was also reported during multistable visual perception (Başar-Eroǧlu, Strüber, Kruse, et al., 1996), that is, spontaneously switching between different interpretations of an invariant stimulus pattern like the famous Necker cube. This frontal gamma activity was stronger for observers experiencing more figure reversals compared to those with a lower reversal rate (Strüber et al., 2000; Strüber et al., 2001), and when observers were required to control their reversal rate intentionally (Mathes et al., 2006). Together, these findings might indicate that frontal gamma band activity represents top-down influences of attentional selection on feature binding of relevant object representations during perceptual reversals (Engel et al., 2001).
Overall, these example studies on induced gamma activity demonstrate a variety of gamma-related functions ranging from basic perceptual to high-level cognitive processes like learning, memory, and attention. On the one hand, such a diversity of functional correlates speaks against a role of induced gamma activity for a single specific cognitive function. On the other hand, the processes of perception, recognition, and attention are closely intertwined and, therefore, might rely on the same neurophysiological mechanisms inherent in gamma oscillations that subserve these functions in a dynamic task-dependent manner (Fries, 2009; Tallon-Baudry, 2009; Varela et al., 2001).
GAMMA ACTIVITY IN SENSORY AND COGNITIVE PROCESSING 153
## **8.5 Neurophysiological mechanisms**
How do gamma oscillations exert their functions in basic sensory and higher cognitive functions and what are the neurophysiological mechanisms underlying oscillatory gamma activity?
The central concept which is thought to underlie the functional relevance of gamma activity is referred to as "oscillatory synchrony", that is, the periodic co-occurrence of electrical impulses from a group of neurons on a fine temporal scale. In the context of EEG scalp recordings, the obtained electrophysiological data inevitably reflect synchronized activity from large neuronal populations, because otherwise the weak synaptic currents would not be measurable at the scalp level. Local oscillatory synchrony resulting from within-area interactions would then appear as increased power at individual electrodes, whereas oscillatory synchrony related to large-scale integration is best characterized by phase coherence between two distant sources (Siegel et al., 2012; Varela et al., 2001).
Oscillatory synchrony is thought to temporally structure the occurrence of spike trains without changing the mean firing rates of neurons and, thereby, to have a functional role in the processing of incoming inputs and the emergence of functional networks by gating the information flow (Salinas & Sejnowski, 2001). Converging evidence from experimental work in animals (in vivo and in vitro) and modeling approaches suggests that cortical gamma oscillations and their local synchronization result from interactions of reciprocally connected excitatory pyramidal cells and inhibitory gamma-aminobutyric acid (GABA)-ergic interneurons (Bartos et al., 2007; Buzsáki & Wang, 2012; Wang, 2010; Whittington et al., 2011; Whittington et al., 2000).
In such a network, the pyramidal cells activate the interneurons, which selfgenerate synchronized gamma oscillations. This gamma-synchronized activity of the interneurons is then imposed onto the pyramidal cells, resulting in rhythmic inhibition of the pyramidal cells, which in turn leads to a rhythmic synchronization of their discharges. Thus, during each cycle of these excitatory-inhibitory feedback loops, the time window during which the pyramidal cells are able to discharge is restricted by the decay time of their inhibitory input from the fast-spiking interneurons, introducing a phase delay of a few milliseconds between pyramidal and interneuron discharges (Fries et al, 2007). From this basic mechanism of gamma synchronization several mechanistic consequences arise that are thought to be instrumental for the formation of neuronal cell assemblies, cortical signal transmission, and, thereby, the implementation of cognitive functions (Bosman et al., 2014; Cannon et al., 2014; Vinck & Bosman, 2016).
One consequence of gamma synchronization that relates to assembly formation is its involvement in the regulation of synaptic plasticity. The precise timing of pre- and post-synaptic processes emerging from gamma synchronization acts on a time scale of a few tens of milliseconds, which is relevant for spike-timing-dependent plasticity and, thus, for the induction of long-term potentiation or depression (Fell & Axmacher, 154 DANIEL STRÜBER and CHRISTOPH S. HERRMANN
2011; Paulsen & Sejnowski, 2000; Sejnowski & Paulsen, 2006) and associative learning (Miltner et al., 1999). It has been proposed that the period of gamma oscillations (~25 msec) is "designed" to match the time course of calcium fluctuations in dendrites and, therefore, to facilitate learning (Bibbig et al., 2001).
With regard to local within-area interactions, synchronization in the gamma-band with its high temporal precision in the millisecond range is hypothesized to increase the impact of presynaptic neurons on their target cells because the gamma-synchronized spike packages arrive close together, thus summing up more effectively to initiate postsynaptic discharges. This effect of precise spike timing is referred to as feedforward coincidence detection (Fries, 2009; Salinas & Sejnowski, 2001), which has been linked to the integration (binding) of different stimulus features during object recognition (Bosman et al., 2014).
This concept has also been transferred to inter-areal communication between multiple groups of neurons, each oscillating in the gamma frequency range. In this context, the "communication through coherence" (CTC) hypothesis (Fries, 2005; 2015) claims that the communication between two groups of neurons can be facilitated by gamma synchronization in the two groups, if the spikes from the presynaptic group (sender) arrive at the postsynaptic group (receiver) at the appropriate phase, that is, during a minimal amount of GABAergic inhibition. This phase-coupling of oscillations constitutes a window of "opportunity" in which neural networks jointly involved in signal processing can communicate. This mechanism allows for gain modulation of pre-synaptic inputs that compete for activating higher-level post-synaptic targets as is the case with selective attention. In this scenario, visual attention might selectively increase the effective strength of those synaptic inputs from lower level neurons that process attended stimuli at the expense of inputs from the non-attended stimuli (Bosman et al., 2014; Fries, 2015). In this way, gamma synchronization might dynamically route the information flow between higher and lower level areas within the visual hierarchy as has been observed locally between multiple visual areas (see, for review, Bosman et al., 2014).
However, it is less clear whether gamma synchronization also serves as a mechanism for large-scale integration across distant brain regions that also include, for example, frontal or parietal areas. It has been suggested that the spatial distance between interacting brain areas and, hence, the conduction delay may define the communication frequency, with gamma oscillations acting more locally and lower frequencies more globally (Kopell et al., 2000; von Stein & Sarnthein, 2000). A reason for this may be that, in contrast to the millisecond precision of gamma oscillations, lower-frequency bands are more robust to spike timing delays (Buschman & Miller, 2007). Indeed, several findings in monkeys have shown that long-distance top-down processes are carried by interareal synchrony in the alpha and low-beta frequency range, whereas gamma oscillations index a local encoding of information and the bottom-up transfer of low-level sensory information to higher-level areas (for reviews, see, Bressler & Richter, 2015; Gregoriou et al., 2015; Siegel et al., 2012; Wang, 2010).
On the other hand, there is also increasing evidence for a role of gamma synchrony in large-scale interaction during various perceptual and attentional processes (see GAMMA ACTIVITY IN SENSORY AND COGNITIVE PROCESSING 155
for a review, Gregoriou et al., 2015), indicating that physical distance might not be the only factor that determines the frequency band used for inter-areal synchronization. Moreover, gamma-synchronized long-range signal transmission seems to work both upstream (i.e., bottom-up) and downstream (i.e., top-down) within the cortical hierarchy. For example, long-range gamma coupling between prefrontal and visual areas during directed attention was found to be initiated frontally, thereby signaling topdown attentional influences on the visual cortex (Gregoriou et al., 2009). Another study reported long-range bottom-up directed gamma synchrony between posterior parietal and prefrontal regions during automatic attention driven by salient stimuli (Buschman & Miller, 2007). Intriguingly, the same areas synchronized in top-down direction if attention was focused volitionally, but in this case in the beta-range (Buschman & Miller, 2007), indicating that different frequencies are used for feedforward and feedback signaling.
Such frequency-specific differences in the direction of inter-areal interaction (i.e., bottom-up vs. top-down) have been related to the different directions of information flow in the cortical layers with feedforward and feedback connections originating primarily in superficial and deep layers, respectively (Felleman & Van Essen, 1991; Markov et al., 2014). Accumulating evidence suggests that alpha/beta oscillations originate in deeper layers of the visual cortex and support feedback signaling, whereas gamma synchrony emerges from superficial layers and signals feedforward information flow (Buffalo et al., 2011; Michalareas et al., 2016; van Kerkoerle et al., 2014; von Stein et al., 2000). Together, these findings clearly suggest a role for gamma synchrony in local bottom-up interaction between visual cortices (Siegel et al., 2012). However, it remains an open question how this function can be reconciled with the documented long-range gamma synchrony during top-down attention (Gregoriou et al., 2015).
Overall, the recurrent excitatory-inhibitory network interactions underlying local gamma synchronization are thought to establish low-level circuit functions (e.g., synaptic plasticity, coincidence detection, gain modulation, phase coding, dynamic routing) that may act as elementary building blocks of cognitive functions (e.g., visual feature integration, selective attention, learning, and memory) in a task-specific combination (Bosman et al., 2014; Siegel et al., 2012). Nevertheless, there are multiple methodological concerns that need to be considered to reliably assess EEG gamma activity as outlined in the next section.
# **8.6 Methodological aspects**
Scalp recorded gamma activity is subject to a variety of high-frequency artefacts which might seriously affect recording, analysis, and interpretation of the data. Therefore, these artefacts need to be either prevented by appropriate recording conditions or to be removed by post hoc analysis techniques. There are two main sources of artefacts. First, technical artefacts like power line noise, the screen refresh rate, or the rate at which 156 DANIEL STRÜBER and CHRISTOPH S. HERRMANN
single images are presented in order to show a movie (cf. Figure 8.2 right panel, SSVEP). Second, physiological artefacts like eye movements and electromyogenic (EMG) activity generated by muscles from the scalp, face, and neck (see, for review, Nottage & Horder, 2016).
## **8.7 Technical artefacts**
Power line noise occurs at a frequency of 50 Hz in Europe and 60 Hz in the US; both frequencies are in the gamma range. Therefore, any power supply like electric cables, wall sockets, or electrically operated equipment inside the recording cabin (lamps) results in a 50-or 60-Hz peak in the EEG power spectrum. To effectively avoid frequency interference, experiments should be conducted in an electrically shielded room with all devices inside the cabin operated on batteries. The stimulation monitor can be placed outside the cabin behind an electrically shielded window and a fiberoptic cable can be used to transfer the EEG data to a computer outside the recording cabin. If it is not possible to prevent power line noise from being recorded, a low-pass or "notch" filter at 50 or 60 Hz might be applied to the data. However, the use of such filters is problematic because they might induce "ringing" (i.e., the induction of spurious oscillations by transients in the EEG) and distort the phase of neural oscillations. Alternative strategies have been developed on the basis of noise cancellation (see Nottage, 2010 for details).
In addition to power line noise, every screen refresh generates an electromagnetic signal which might be seen as a narrow band in the EEG gamma range, typically at anterior electrodes. The exact frequency depends on the primary refresh rate and its harmonics. Nottage & Horder (2016) explore possible ways to remove this type of artefact.
## **8.8 Physiological artefacts**
The difficulty of properly removing EMG artifacts is particularly important for studies on gamma activity, given the fact that the broad frequency spectrum of EMG activity substantially overlaps with the gamma frequency range. An amplitude maximum of EMG contamination in the gamma range (40–80 Hz) was found at temporal sites during phasic contraction of facial muscles (Goncharova et al., 2003). Because of their high amplitude, occasionally occurring phasic muscle contractions (e.g., chewing or jaw clenching) can be detected relatively easily by visual inspection or mathematical algorithms and then be omitted from further analysis (e.g., Fitzgibbon et al., 2015). However, in addition to large phasic contractions, the head and neck muscles are constantly active to maintain posture, which might result in tonic EMG activity throughout an EEG session.
GAMMA ACTIVITY IN SENSORY AND COGNITIVE PROCESSING 157
Critically, low-amplitude tonic muscle activity occurs even in "relaxed" states and is, thus, difficult to detect in scalp recordings but still contributes significantly to EMG contamination in the gamma range, as has been shown in pharmacologically paralyzed human volunteers (Whitham et al., 2007). Paralysis compared to pre-paralyzed states of the same participants was found to result in a marked reduction of spectral power in the gamma range, with 84% of the power derived from EMG, mostly over peripheral scalp regions. Moreover, the execution of different cognitive tasks induced a broadband increase in the gamma frequency range in unparalyzed but not paralyzed participants, indicating that EMG activity was responsible for the task-related spectral power increases (Whitham et al., 2008). However, when employing a standard oddball task that allows for stimulus-locked data analysis, significant gamma activity was identified in both the pre-paralyzed and the paralyzed condition, with stronger activity for rare target than for more frequent standard stimuli (Pope et al., 2009).
While these studies clearly demonstrate a large contribution of EMG activity to the overall EEG spectral power, they also show that (at least under experimental conditions where time- and stimulus-locked analysis is possible, and in contrast to, for example, analyzing states of varying cognitive load during mental arithmetic) neuronal gamma activity can still be measured at the scalp EEG. Thus, it seems possible to extract neural gamma activity from EMG noise if it is analyzed in response to discrete stimuli (e.g., coherent stimuli vs. incoherent visual objects). For this, however, methods for the effective removal of EMG artefacts are required.
There is a multitude of methods for dealing with scalp EMG (see, for review, Nottage & Horder, 2016). One novel approach that specifically addresses the tonic nature of scalp and neck muscle artefacts uses mathematical modeling to fit individual muscle spikes and subtract these from the signal, resulting in an effective correction of the gamma activity associated with a self-paced motor task (Nottage et al., 2013). Recently, Janani and colleagues (2018) used datasets that are free of muscle activity due to paralysis (taken from Whitham et al., 2007, 2008) to identify limitations of traditional approaches and, then, to evaluate the improvements of a newly developed algorithm for tonic muscle artefact removal. With this method, high-frequency EMG artefacts were reduced considerably, although a residual artefact still remains (compared to paralysis). Given the variety of techniques that are based on different mathematical concepts, the authors suggested using a combination of complementary algorithms for a further improvement of EMG artefact removal (Janani et al., 2018).
Ocular activity also generates muscle-related artefacts. The main sources of eye movement artefacts are blinks and saccades. It is standard practice to measure the electro-oculogram (EOG) from two channels of the left and right eye. For rejecting eye blinks and large saccades, an amplitude threshold is usually set (e.g., 50 µV), which is then used by an algorithm to exclude contaminated EEG trials in any channel from further analysis. This automatic amplitude threshold procedure is then complemented by visual inspection of all epochs. For algorithms based on eye tracking data that detect and correct eye blinks and other ocular artifacts in a fully automated fashion, see Plöchl et al., 2012.
158 DANIEL STRÜBER and CHRISTOPH S. HERRMANN
Blink artefacts elicit a large potential with a predominantly frontal topography and are easy to identify in the vertical electro-oculogram (VEOG). Saccades are generated by a pair of extra-ocular muscles which contract to move the eyeball, thereby inducing a saccadic spike potential in the EEG at the onset of each saccade (Thickbroom & Mastaglia, 1985). Saccadic spike potentials are too small to be detected by standard amplitude thresholds for automatic EOG-artefact removal, especially in case of microsaccades which are produced during attempted fixation (Martinez-Conde et al., 2013). In their seminal paper, Yuval-Greenberg and colleagues (2008) suspected that high-frequency EEG activity that had been regarded as induced gamma activity in fact reflects microsaccade-induced muscle artefacts. Naturally, this report triggered an intense debate within the field of induced gamma activity research (Schwartzman & Kranczioch, 2011). Section 8.9 summarizes the main points.
# **8.9 Microsaccades and induced gamma activity**
Microsaccades are small (up to 1 degree), jerk-like saccades with a duration of about 25 ms and an average rate of 1–2 per second (Martinez-Conde et al., 2013). There are at least three important similarities between microsaccades and induced gamma activity that need to be considered. First, in response to a sudden change in stimulus input, the microsaccade rate shows a characteristic biphasic time course, with an early inhibition phase peaking at 100–150 ms after stimulus onset, followed by a rebound phase peaking between 200 and 400 ms after stimulus onset (Engbert, 2006). Thus, the rebound phase of microsaccades corresponds to the time window where induced gamma activity typically appears.
Second, the rate of microsaccades is modulated by perceptual and cognitive factors that have also been linked to induced gamma activity, including attention and memoryrelated processes (Engbert & Kliegl, 2003; Valsecchi et al., 2007; Valsecchi et al., 2009), physical stimulus features like color and luminance contrast (Rolfs et al., 2008), and the coherence of objects (Yuval-Greenberg et al., 2008). Thus, microsaccade rate represents a true confound in experiments on gamma activity since modulations of microsaccade rate and gamma activity might generate an identical pattern of results across experimental conditions. For example, both microsaccade rate and induced gamma power show increased responses to a coherent object in comparison to an incoherent object.
Third, depending on the location of the reference electrode, the frontally occurring microsaccade-induced saccadic spike potential translates into a broadband (~20–90 Hz) gamma power increase with a maximum at centro-parietal and occipital electrodes, that is, regions where it strongly coincides with induced gamma activity (Reva & Aftanas, 2004; Yuval-Greenberg et al., 2008). Thus, saccadic spike potentials mimic not only the frequency content of induced gamma activity but also its typical topography. GAMMA ACTIVITY IN SENSORY AND COGNITIVE PROCESSING 159
Notably, this can be avoided by using MEG, since it does not require a reference (Gruber et al., 2008).
These similarities between microsaccades and induced gamma activity regarding their sensitivity to cognitive effects as well as their temporal, topographical and spectral properties have been convincingly demonstrated and have led to the suggestion that—at least in some cases—induced gamma activity reflect saccadic spike potentials rather than a neural response (Yuval-Greenberg et al., 2008). This also concerns earlier EEG findings that might have been erroneously interpreted as neuronal gamma activity, when in fact they reflected microsaccade-induced spike potential artefacts (Keren et al., 2010). How strong previous EEG findings might be affected by microsaccades depends on several aspects, for example, the exact time window of the effects (in relation to the saccadic rebound), the broadness of the gamma response (in relation to the 20–90 Hz spike potential), and the choice of the reference electrode, given its influence on the topography, to name but a few ( for further details, see Schwartzman & Kranczioch, 2011).
Notably, evoked gamma activity is not affected by microsaccade-induced spike potential artefacts. One reason is that evoked gamma activity occurs much earlier than the microsaccade rebound after sensory stimulation. Another reason is that spike potentials, in contrast to the evoked gamma activity, are not tightly time-locked to the stimulus and, thus, cancel out during averaging of the evoked potential (Yuval-Greenberg & Deouell, 2009).
Although Yuval-Greenberg and colleagues (2008) did not deny the existence of induced gamma activity and its role in perception and cognition in general, their findings posed a challenge to develop methods for separating the effects of microsaccades and induced gamma responses in EEG scalp recordings. One immediate consequence of this study was the necessity to use eye tracking with sufficient spatial and temporal resolution for detecting microsaccades as small as 0.15° visual angle, given that even precise fixation of a continuously present fixation point does not preclude microsaccade-related brain activity (Dimigen et al., 2009). The rationale behind a combined recording of EEG and eye tracking data is to demonstrate that differences of induced gamma activity and microsaccade rate do not covary across conditions and, thus, effects of induced gamma activity cannot easily be explained by microsaccadic muscle potentials. Indeed, such differential modulations of gamma activity and microsaccades time courses have been reported, for example, during object motion (Naue et al., 2011) and memory-based object recognition (Hassler et al., 2013).
However, high-resolution eye trackers are expensive and not always available. Alternatively, there are methods available allowing for offline artefact correction that identify saccadic spike potentials via EOG sensors, that is, without the need of an eye tracker (Hassler et al., 2011; Keren et al., 2010; Nottage, 2010). However, Keren and colleagues (2010) used eye tracking in addition to EOG-based detection of microsaccades to evaluate the hit and false alarm rates of several spatiotemporal filters that were applied to the EOG data to identify the sharp amplitude increase at the onset of saccadic spike potentials. With this method, detection rates of 80% on average could be achieved for microsaccades of at least 0.2°, which were then efficiently attenuated by means of mathematical algorithms. For artifact correction methods based on combined 160 DANIEL STRÜBER and CHRISTOPH S. HERRMANN
EEG and eye tracking recordings, see also Plöchl et al. (2012). Nottage (2010) and Hassler and colleagues (2011) used different mathematical approaches but both have been demonstrated to effectively remove microsaccadic muscle artefacts, resulting in a more sustained and narrow-band gamma signal of the residual activity compared to the frequency plot of the saccadic spike potential (see, for review, Nottage & Horder, 2016).
Although the available methods are relatively easy to apply and effective in reducing saccadic spike potentials, they do not remove the artefact completely and they do not attenuate saccade-related visual brain activity (Dimigen et al., 2009; Plöchl et al., 2012). Also, the fundamental problem of the confounding co-modulation of induced gamma activity and microsaccade rate cannot be solved by artefact correction techniques. Therefore, it has been suggested recently to reduce the occurrence of microsaccades and related confounds in the EEG at the level of experimental design instead of applying offline correction methods (Tal & Yuval-Greenberg, 2018). Considerably reducing the incidence of microsaccades during experimentation would allow rejecting microsaccades rather than just correcting artefactual trials and still leaving enough (then artefact-free) trials for analysis. As a first step, Tal and Yuval-Greenberg (2018) were able to reduce the average number of saccades (including microsaccades) by 10–25% through manipulation of different task characteristics (e.g., by adding a foveal task, whereas the stimulus of interest was parafoveal). However, it remains to be seen how this approach can be applied to the diverse experimental setups covering the full range of induced gamma activity related cognitive processes.
In summary, together with other muscle artefacts, microsaccades impose a serious difficulty on the analysis and interpretation of induced gamma activity in human EEG. To separate activity related to saccadic spike potentials from induced gamma activity, using high-resolution eye tracking is recommended as the most reliable way to identify microsaccades. However, there are also techniques available to use EOG data for saccadic spike potential detection. In a second step, off-line artefact removal methods should be used to correct artefactual trials. Rejecting all artefactual trials is currently not possible due to the high prevalence of microsaccades in typical visual experiments, but there are suggestions how to reduce the number of microsaccades through experimental design. Current evidence from artefact-corrected data confirms the influence of microsaccades on induced gamma activity, but also indicates the existence of induced gamma activity that survived artifact suppression, thereby replicating earlier findings on the functional roles of induced gamma activity in, for instance, object representation (Hassler et al., 2013; 2011). Finally, depending on the research question at hand, a further option to prevent microsaccadic contamination of gamma activity might be to restrict the analyses to the evoked gamma activity, which is not affected (e.g., Lally et al., 2014).
## **8.10 Clinical relevance**
Given its role in multiple cognitive processes and neural information integration, disturbed gamma activity might reflect an important pathophysiological mechanism GAMMA ACTIVITY IN SENSORY AND COGNITIVE PROCESSING 161
underlying the mental deficits of patients suffering from diverse neuropsychiatric disorders (Başar, 2013; Herrmann & Demiralp, 2005; Uhlhaas & Singer, 2006). One of the most extensively studied disorders in relation to gamma activity is schizophrenia (Uhlhaas & Singer, 2010) (see also Chapter 18), which is characterized by positive symptoms like hallucinations, delusions, and thought disorders, as well as negative symptoms like reduced affect, motivation, and behavior. Positive symptoms have been generally linked to increased gamma activity, whereas negative symptoms correlate with a decrease of gamma activity compared to healthy controls (Herrmann & Demiralp, 2005). Moreover, as a group, schizophrenic patients have deficits in both basic sensory and cognitive functions, which have been related to evoked and induced gamma activity.
For instance, early evoked gamma activity in response to auditory stimulation was found to be reduced in schizophrenic patients receiving medication (Leicht et al., 2010; Lenz et al., 2011), but not in unmedicated patients (Gallinat et al., 2004). Başar-Eroǧlu and colleagues (2011) reported that auditorily evoked gamma responses did not differ between schizophrenic patients and healthy controls, but on the single-trial level, gamma responses were higher in patients compared to controls. Modality-specific effects were found for chronic medicated patients, demonstrating reduced early evoked gamma activity for visual but not auditory stimulation (Spencer et al., 2008). Seemingly, more research is needed to get a clearer picture regarding the role of early evoked gamma activity in sensory processing of schizophrenic patients.
With regard to induced gamma activity in schizophrenic patients, most of the evidence points to impaired gamma activity related to higher perceptual and cognitive functions (see, for review, Uhlhaas & Singer, 2010; 2012). This includes, for example, cognitive control in first-episode schizophrenia patients with and without medication (Minzenberg et al., 2010), and working memory (Haenschel et al., 2009), although one study found working memory-related gamma amplitudes to be preserved in patients but lacking any relation to task difficulty, as present in normal controls (Basar-Eroǧlu et al., 2007). Reduced amplitudes or reduced phase locking of gamma oscillations during working memory and other cognitive tasks have been found predominantly in frontal areas which corresponds to the frequently reported hypo-frontality in schizophrenia (see, for review, Senkowski & Gallinat, 2015).
Interestingly, a recent review on gamma activity in first episode psychosis patients and people at high risk for psychosis found a similar decrease of evoked and induced gamma activity as has been reported for chronic schizophrenia (Reilly et al., 2018), indicating that reduced gamma activity in the early phase of psychosis might serve as a biomarker or endophenotype allowing for an early intervention before the disorder has fully developed. This, however, would require a more standardized procedure regarding the employed experimental paradigms and measures of gamma activity.
Alternatively, spontaneous or resting-state gamma activity might be used as a biomarker of schizophrenia, which would bear the advantage that it can be recorded without engagement in a task (i.e., spontaneous activity) or as pre-stimulus baseline activity (i.e., resting-state). Indeed, there is evidence for altered spontaneous/resting 162 DANIEL STRÜBER and CHRISTOPH S. HERRMANN
gamma activity in schizophrenia. But in contrast to the reported reduction of evoked and induced gamma activity, this type of gamma activity has been found to be predominantly increased in chronic schizophrenic patients (Spencer, 2012; see, for review, White & Siegel, 2016) as well as in first episode patients and high-risk populations (Reilly et al., 2018). While it has been proposed that increased spontaneous/resting gamma activity contributes to positive symptoms like hallucinations (White & Siegel, 2016), its relation to negative symptoms and reduced gamma activity during stimulus processing is less clear. Thus, different computational models have been discussed regarding the neurophysiological mechanisms underlying gamma activity increases during resting state and gamma decreases during stimulus processing in schizophrenia (Jadi et al., 2016). In general, abnormal gamma activity in schizophrenia has been related to dysfunctional circuit mechanisms responsible for generating gamma oscillations, that is, a reduced input from inhibitory GABAergic interneurons to pyramidal cells and/or abnormal glutamatergic input from the pyramidal cells to the interneurons (see, for review, McNally & McCarley, 2016), resulting in a disturbed balance between excitatory and inhibitory mechanisms (E/I balance).
Also in autism spectrum disorders (ASD), abnormal gamma oscillations have been suggested as a potential biomarker for a dysfunctional E/I balance in children with ASD (Stroganova et al., 2015; Uhlhaas & Singer, 2012). Similar to patients with schizophrenia, children with ASD have been consistently characterized by reduced gamma activity during sensory stimulation with overlapping perceptual deficits (see, for review, Uhlhaas & Singer, 2012). Interestingly, children with ASD also show an increase in resting-state gamma activity (van Diessen et al., 2015; Wang et al., 2013) but, unlike schizophrenic patients, do not experience hallucinations. However, despite the substantial overlap between schizophrenia and ASD regarding the dysfunctional E/I balance and the resulting impairments in cognitive integration, there are important differences with regard to the developmental timing of the changing E/I balance, which might explain some of the unique features of each disorder (Uhlhaas & Singer, 2012; White & Siegel, 2016).
Another neurodevelopmental disorder that is predominantly diagnosed in childhood and adolescence is attention-deficit/hyperactivity disorder (ADHD). According to its core symptoms (inattention, hyperactivity, impulsivity), one might expect a reduction of gamma activity due to the attention deficit and/or a gamma increase due to the hyperactivity component. In one of the first studies on evoked gamma activity in ADHD children, Yordanova and colleagues (2001) reported larger and more strongly phaselocked early evoked gamma activity in ADHD children during an auditory detection task involving a motor response. Gamma augmentations did not differentiate between attended and ignored stimuli. This finding was interpreted as reflecting impaired early auditory processing due to deficient motor inhibition in ADHD children (Yordanova et al., 2001).
Enhanced evoked gamma activity in children with ADHD was also found during stimulus encoding of a visual memory task (Lenz, Krauel, et al., 2008). However, in contrast to healthy children, the encoding-related gamma activity was enhanced GAMMA ACTIVITY IN SENSORY AND COGNITIVE PROCESSING 163
unspecifically, that is, it was unrelated to subsequent recognition performance. Similarly, early evoked gamma activity did not reflect the difference in long-term memory representation between familiar and unfamiliar objects in a simple forced-choice reaction task (Lenz et al., 2010).
In a study by Prehn-Kristensen and colleagues (2015), the distractibility of ADHD patients was assessed in a delayed-match-to-sample paradigm by presenting a distractor stimulus during the delay period, which should be ignored. Children with ADHD but not healthy controls exhibited an increase of occipital early evoked gamma activity in response to the distractor, indicating a higher distractibility resulting in disturbed working memory maintenance already on a very early level of interference processing (Prehn-Kristensen et al., 2015).
Together, these findings might indicate that attentional problems in ADHD are related to early sensory processing deficits as reflected by unspecific evoked gamma increases that might be interpreted as an increase of noise. This may be partially caused by the fact that the same genetic variations within the dopaminergic pathway that have been associated with ADHD, also contribute to enhancements of gamma activity in healthy volunteers (Demiralp et al., 2007; Herrmann & Demiralp, 2005). However, this hyperactivity-based interpretation might be restricted to gamma activity during stimulus or cognitive processing since spontaneous gamma activity was shown to be diminished in children (Barry et al., 2010) and adults (Tombor et al., 2019) with ADHD.
Gamma oscillations have also been associated with neurodegenerative diseases like Parkinson's disease (PD) and Alzheimer's dementia (AD) (Nimmrich et al., 2015). For PD, however, oscillations in the beta range are more directly related to the clinical symptoms than gamma activity and might serve as a biomarker, whereas studies on gamma oscillations in AD yielded divergent findings of reduced as well as enhanced amplitudes, indicating the need for further research before clear statements about the usefulness of gamma oscillations as a biomarker for AD can be made (see, for review, Nimmrich et al., 2015). In two recent studies on AD, Başar and colleagues employed a target detection task and simple visual stimulation to analyze gamma activity within three sub-bands over four time windows and found a decreased response to visual stimuli and a delayed gamma response to target stimuli compared to healthy controls (Başar et al., 2016), as well as an abnormal increase of gamma coherence for AD patients in both conditions (Başar et al., 2017).
Overall, AD and many other neuropsychiatric disorders are characterized by aberrant gamma activity pointing to dysfunctional oscillatory network activities that are regulated by inhibitory interneurons (see, for reviews, Palop & Mucke, 2016; Ruden et al., 2021). While such an interneuron impairment might indeed represent a common mechanism of cognitive dysfunction in diverse neuropsychiatric disorders, the use of gamma oscillations as a single oscillatory biomarker is limited due to its lack of specificity (see, however, Lenz et al., 2011 for a study on the specificity of gamma activity in neuropsychiatric disorders). Therefore, it might be important to look for interactions with other frequency bands to create oscillatory biomarkers that are more specific for each disorder (Başar et al., 2013; Başar, Schmiedt-Fehr, et al., 2016; Uhlhaas & Singer, 2012).
164 DANIEL STRÜBER and CHRISTOPH S. HERRMANN
Notably, however, there is recent evidence from a mouse model of AD that impaired gamma oscillations are specifically related to a hallmark of AD, that is, the abnormal aggregation of plaque-forming proteins (amyloid-beta protein) in the brain (Iaccarino et al., 2016). The authors found that inducing gamma oscillations by a 40-Hz flickering light led to a major reduction of plaques in the visual cortex of the exposed mice and to an activation of microglia (i.e., immune cells in the brain) that degrade the plaques (Iaccarino et al., 2016). Crucially, later studies using different forms of sensory gamma stimulation in multiple AD mouse models could not only demonstrate a clear link between gamma activity and cellular metabolism but also improvements of cognitive functions like learning and memory, suggesting a therapeutic role of gamma entrainment in AD (see, for review, Adaikkan & Tsai, 2020). There is emerging evidence that similar cognitive effects can be achieved in humans by employing non-invasive brain stimulation techniques that could, in contrast to rhythmic sensory stimulation, target higher-order cognitive brain areas linked more directly to core symptoms of the disorder than sensory cortices (Benussi et al., 2021; see, for reviews, Bréchet et al., 2021, and Strüber & Herrmann, 2020).
## **8.11 Challenges and future directions**
There are a number of challenges in relation to the ubiquitous role of gamma oscillations for cognitive functions. For instance, it has been criticized that the power of gamma oscillations is low and inconsistent and that its frequency and power depend on lowlevel stimulus features like size or contrast, which seems to be incompatible with the proposed role of gamma synchronization in cortical processing (Ray & Maunsell, 2015). However, there is also recent reconciling evidence in support of a functional role for gamma synchronization (Singer, 2018).
One related issue regarding the functions of gamma activity in sensory and cognitive processing as well as in clinical contexts is that most of the evidence is correlative in nature. Therefore, it remains unclear whether gamma oscillations and their synchronization are truly relevant for information processing in the brain or whether they merely reflect a by-product of brain organization. It has been argued that even gamma oscillations as such may be a functional epiphenomenon arising from network activities supporting the excitatory-inhibitory balance necessary for normal brain functioning (Merker, 2013). Although this argumentation might reflect a "category mistake" since gamma oscillations cannot be functionally separated from the circuit mechanisms that generate them (Bosman et al., 2014), the necessity remains to go beyond correlations and to demonstrate that gamma activity is causally involved in cortical information processing and cognitive functions.
Causal evidence for a role of gamma oscillation in cognitive processes can be provided by demonstrating that modulating gamma power or coherence improves cognitive outcomes. There are several established methods to modulate brain oscillations, GAMMA ACTIVITY IN SENSORY AND COGNITIVE PROCESSING 165
including rhythmic sensory (steady-state) stimulation, EEG neurofeedback, and noninvasive brain stimulation like repetitive transcranial magnetic stimulation (rTMS; see, for a methods overview, Herrmann et al., 2016). Whereas rTMS is not considered safe for stimulation in the gamma frequency range due to its risk of inducing epileptic seizure (Rossi et al., 2009), steady-state visual stimulation has been successful in entraining gamma oscillations (Herrmann, 2001; Regan, 1968) and improving bindingrelated perceptual performance (Elliott et al., 2000). However, whereas most human EEG studies using rhythmic visual stimulation obtained effects restricted to early visual cortex, EEG-based neurofeedback allows for direct neurocognitive modulation of those brain regions that are crucially involved in specific tasks (see, for review, Enriquez-Geppert et al., 2013).
Neurofeedback training to increase EEG gamma oscillations has been shown to improve perceptual processing (Salari et al., 2014), cognitive control and intelligence measures (Keizer et al., 2010; Keizer, Verschoor, et al., 2010), indicating a functional role of gamma activity for these cognitive processes. However, gamma neurofeedback is technically challenging due to its susceptibility to muscle and ocular artefacts (see Section 8.8). Indeed, there are reports that participants of a neurofeedback training were able to control the feedback signal by activating their head and neck muscles, which might serve as a caveat when designing neurofeedback studies, especially if EEG recordings are used (Merkel et al., 2018). Furthermore, neurofeedback is an endogenous technique that needs to be learned and not all participants might be able to do this, especially patients.
A recent method of non-invasive brain stimulation, called transcranial alternating current stimulation (tACS) avoids these problems by applying sinusoidal currents to stimulate the brain exogenously (see Chapter 22). Its effectiveness in modulating gamma oscillations during motor, sensory and a wide range of high-level cognitive processes has been demonstrated recently (see, for a review, Strüber & Herrmann, 2020). Thus, we propose that tACS might be the appropriate method not only to provide causal evidence for a role of gamma oscillations in brain processing but also to improve gamma activityrelated sensory and cognitive functioning in healthy volunteers and clinical populations (Herrmann & Strüber, 2017; Strüber & Herrmann, 2020).
#### **REFERENCES**
Adaikkan, C. & Tsai, L.-H. (2020). Gamma entrainment: Impact on neurocircuits, glia, and therapeutic opportunities. *Trends in Neurosciences, 43*(1), 24–41. [https://doi.org/10.1016/](https://doi.org/10.1016/j.tins.2019.11.001) [j.tins.2019.11.001](https://doi.org/10.1016/j.tins.2019.11.001)
Adrian, E. D. (1942). Olfactory reactions in the brain of the hedgehog. *Journal of Physiology*, *100*(4), 459–473.
Adrian, E. D. (1950). The electrical activity of the mammalian olfactory bulb. *Electroencephalography and Clinical Neurophysiology*, *2*, 377–388.
Barry, R. J., Clarke, A. R., Hajos, M., McCarthy, R., Selikowitz, M., & Dupuy, F. E. (2010). Resting-state EEG gamma activity in children with attention-deficit/hyperactivity disorder. *Clinical Neurophysiology*, *121*(11), 1871–1877.
166 DANIEL STRÜBER and CHRISTOPH S. HERRMANN
- Bartos, M., Vida, I., & Jonas, P. (2007). Synaptic mechanisms of synchronized gamma oscillations in inhibitory interneuron networks. *Nature Reviews Neuroscience*, *8*(1), 45–56.
- Başar, E. (2013). A review of gamma oscillations in healthy subjects and in cognitive impairment. *International Journal of Psychophysiology*, *90*(2), 99–117. [http://doi.org/10.1016/j.ijpsy](http://doi.org/10.1016/j.ijpsycho.2013.07.005) [cho.2013.07.005](http://doi.org/10.1016/j.ijpsycho.2013.07.005)
- Başar, E., Başar-Eroǧlu, C., Güntekin, B., & Yener, G. G. (2013). Brain's alpha, beta, gamma, delta, and theta oscillations in neuropsychiatric diseases: Proposal for biomarker strategies. *Supplements to Clinical Neurophysiology*, *62*, 19–54. [http://doi.org/10.1016/](http://doi.org/10.1016/B978-0-7020-5307-8.00002-8) [B978-0-7020-5307-8.00002-8](http://doi.org/10.1016/B978-0-7020-5307-8.00002-8)
- Başar, E., Emek-Savaş, D. D., Güntekin, B., & Yener, G. G. (2016). Delay of cognitive gamma responses in Alzheimer's disease. *NeuroImage: Clinical*, *11*, 106–115. [http://doi.org/10.1016/](http://doi.org/10.1016/j.nicl.2016.01.015) [j.nicl.2016.01.015](http://doi.org/10.1016/j.nicl.2016.01.015)
- Başar, E., Femir, B., Emek-Savaş, D. D., Güntekin, B., & Yener, G. G. (2017). Increased long distance event-related gamma band connectivity in Alzheimer's disease. *NeuroImage: Clinical*, *14*, 580–590.
- Başar, E., Gönder, A., Özesmi, C., & Ungan, P. (1975). Dynamics of brain rhythmic and evoked potentials. II. Studies in the auditory pathway, reticular formation and hippocampus during the waking stage. *Biological Cybernetics*, *20*(3-4), 145–160.
- Başar, E., Gönder, A., & Ungan, P. (1976). Important relation between EEG and brain evoked potentials. I. Resonance phenomena in subdural structures of the cat. *Biological Cybernetics*, *25*(1), 27–40.
- Başar, E. & Özesmi, C. (1972). The hippocampal EEG-activity and a systems analytical interpretation of averaged evoked potentials of the brain. *Kybernetik*, *12*, 45–54.
- Başar, E., Schmiedt-Fehr, C., Mathes, B., Femir, B., Emek-Savaş, D. D., Tülay, E., Tan, D., Düzgün, A., . . . Başar-Eroǧlu, C. (2016). What does the broken brain say to the neuroscientist? Oscillations and connectivity in schizophrenia, Alzheimer's disease, and bipolar disorder. *International Journal of Psychophysiology*, *103*, 135–148. [http://doi.org/10.1016/j.ijpsy](http://doi.org/10.1016/j.ijpsycho.2015.02.004) [cho.2015.02.004](http://doi.org/10.1016/j.ijpsycho.2015.02.004)
- Başar-Eroǧlu, C., Brand, A., Hildebrandt, H., Karolina Kedzior, K., Mathes, B., & Schmiedt, C. (2007). Working memory related gamma oscillations in schizophrenia patients. *International Journal of Psychophysiology*, *64*(1), 39–45. [http://doi.org/10.1016/j.ijpsy](http://doi.org/10.1016/j.ijpsycho.2006.07.007) [cho.2006.07.007](http://doi.org/10.1016/j.ijpsycho.2006.07.007)
- Başar-Eroǧlu, C., Mathes, B., Brand, A., & Schmiedt-Fehr, C. (2011). Occipital γ response to auditory stimulation in patients with schizophrenia. *International Journal of Psychophysiology*, *79*, 3–8.
- Başar-Eroǧlu, C., Strüber, D., Kruse, P., Başar, E., & Stadler, M. (1996). Frontal gamma-band enhancement during multistable visual perception. *International Journal of Psychophysiology*, *24*(1-2), 113–125. [http://doi.org/10.1016/S0167-8760\(96\)00055-4](http://doi.org/10.1016/S0167-8760(96)00055-4)
- Başar-Eroǧlu, C., Strüber, D., Schürmann, M., Stadler, M., & Başar, E. (1996). Gamma-band responses in the brain: A short review of psychophysiological correlates and functional significance. *International Journal of Psychophysiology*, *24*(1-2), 101–112. [http://doi.org/10.1016/](http://doi.org/10.1016/S0167-8760(96)00051-7) [S0167-8760\(96\)00051-7](http://doi.org/10.1016/S0167-8760(96)00051-7)
- Benussi, A., Cantoni, V, Cotelli, M. S., Cotelli, M., Brattini, C., Datta, A., Thomas, C., Santarnecchi, E., Pascual-Leone, A., & Borroni, B. (2021). Exposure to gamma tACS in Alzheimer's disease: A randomized, double-blind, sham-controlled, crossover, pilot study. *Brain Stimulation*, *14*, 531–540.
GAMMA ACTIVITY IN SENSORY AND COGNITIVE PROCESSING 167
- Berger, H. (1929). Über das Elektrenkephalogramm des Menschen, I. Mitteilung. *Archiv Für Psychiatrie Und Nervenkrankheiten*, *87*(4), 527–570.
- Berger, H. (1934). Über das Elektrenkephalogramm des Menschen, IX. Mitteilung. *Archiv Für Psychiatrie Und Nervenkrankheiten*, *102*, 538–557.
- Berger, H. (1936). Über das Elektrenkephalogramm des Menschen, XI. Mitteilung. *Archiv Für Psychiatrie Und Nervenkrankheiten*, *104*, 678–689.
- Berger, H. (1937). Über das Elektrenkephalogramm des Menschen, XII. Mitteilung. *Archiv Für Psychiatrie Und Nervenkrankheiten*, *106*, 165–187.
- Bibbig, A., Faulkner, H. J., Whittington, M. A., & Traub, R. D. (2001). Self-organized synaptic plasticity contributes to the shaping of gamma and beta oscillations in vitro. *Journal of Neuroscience*, *21*(22), 9053–9067. [pii]
- Bosman, C. A., Lansink, C. S., & Pennartz, C. M. A. (2014). Functions of gamma-band synchronization in cognition: From single circuits to functional diversity across cortical and subcortical systems. *European Journal of Neuroscience*, *39*(11), 1982–1999. [http://doi.org/](http://doi.org/10.1111/ejn.12606) [10.1111/ejn.12606](http://doi.org/10.1111/ejn.12606)
- Bouyer, J. J., Montaron, M. F., & Rougeul, A. (1981). Fast fronto-parietal rhythms during combined focused attentive behaviour and immobility in cat: Cortical and thalamic localizations. *Electroencephalography and Clinical Neurophysiology*, *51*(3), 244–252. [http://](http://doi.org/10.1016/0013-4694(81)90138-3) [doi.org/10.1016/0013-4694\(81\)90138-3](http://doi.org/10.1016/0013-4694(81)90138-3)
- Bréchet, L., Michel, C. M., Schacter, D. L., & Pascual-Leone, A. (2021). Improving autobiographical memory in Alzheimer's disease by transcranial alternating current stimulation. *Current Opinion in Behavioral Sciences*, 40, 64–71. [https://doi.org/10.1016/j.cob](https://doi.org/10.1016/j.cobeha.2021.01.003) [eha.2021.01.003](https://doi.org/10.1016/j.cobeha.2021.01.003)
- Bressler, S. L. & Freeman, W. J. (1980). Frequency analysis of olfactory system EEG in cat, rabbit, and rat. *Electroencephalography and Clinical Neurophysiology*, *50*(1-2), 19–24. [http://](http://doi.org/10.1016/0013-4694(80)90319-3) [doi.org/10.1016/0013-4694\(80\)90319-3](http://doi.org/10.1016/0013-4694(80)90319-3)
- Bressler, S. L. & Richter, C. G. (2015). Interareal oscillatory synchronization in top-down neocortical processing. *Current Opinion in Neurobiology*, *31*, 62–66. [http://doi.org/10.1016/](http://doi.org/10.1016/j.conb.2014.08.010) [j.conb.2014.08.010](http://doi.org/10.1016/j.conb.2014.08.010)
- Brunet, N., Vinck, M., Bosman, C. A., Singer, W., & Fries, P. (2014). Gamma or no gamma, that is the question. *Trends in Cognitive Sciences*, *18*(10), 507–509. [http://doi.org/10.1016/](http://doi.org/10.1016/j.tics.2014.08.006) [j.tics.2014.08.006](http://doi.org/10.1016/j.tics.2014.08.006)
- Buffalo, E. A., Fries, P., Landman, R., Buschman, T. J., & Desimone, R. (2011). Laminar differences in gamma and alpha coherence in the ventral stream. *Proceedings of the National Academy of Sciences of the United States of America*, *108*(27), 11262–11267.
- Busch, N. A., Debener, S., Kranczioch, C., Engel, A. K., & Herrmann, C. S. (2004). Size matters: Effects of stimulus size, duration and eccentricity on the visual gammaband response. *Clinical Neurophysiology*, *115*(8), 1810–1820. [http://doi.org/10.1016/j.cli](http://doi.org/10.1016/j.clinph.2004.03.015) [nph.2004.03.015](http://doi.org/10.1016/j.clinph.2004.03.015)
- Busch, N. A., Herrmann, C. S., Müller, M. M., Lenz, D., & Gruber, T. (2006). A crosslaboratory study of event-related gamma activity in a standard object recognition paradigm. *NeuroImage*, *33*(4), 1169–1177.
- Busch, N. A., Schadow, J., Fründ, I., & Herrmann, C. S. (2006). Time-frequency analysis of target detection reveals an early interface between bottom-up and top-down processes in the gamma-band. *NeuroImage*, *29*(4), 1106–1116. [http://doi.org/10.1016/j.neuroim](http://doi.org/10.1016/j.neuroimage.2005.09.009) [age.2005.09.009](http://doi.org/10.1016/j.neuroimage.2005.09.009)
168 DANIEL STRÜBER and CHRISTOPH S. HERRMANN
- Buschman, T. J. & Miller, E. K. (2007). Top-down versus bottom-up control of attention in the prefrontal and posterior parietal cortices. *Science*, *315*(5820), 1860–1862. [http://doi.org/](http://doi.org/10.1126/science.1138071) [10.1126/science.1138071](http://doi.org/10.1126/science.1138071)
- Buzsáki, G. & Wang, X.-J. (2012). Mechanisms of gamma oscillations. *Annual Review of Neuroscience*, *35*(1), 203–225.
- Cannon, J., McCarthy, M. M., Lee, S., Lee, J., Börgers, C., Whittington, M. A., & Kopell, N. (2014). Neurosystems: Brain rhythms and cognitive processing. *European Journal of Neuroscience*, *39*(5), 705–719.
- Crone, N. E., Korzeniewska, A., & Franaszczuk, P. J. (2011). Cortical gamma responses: Searching high and low. *International Journal of Psychophysiology*, *79*(1), 9–15.
- Darvas, F., Scherer, R., Ojemann, J. G., Rao, R. P., Miller, K. J., & Sorensen, L. B. (2010). High gamma mapping using EEG. *NeuroImage*, *49*(1), 930–938. [http://doi.org/10.1016/j.neuroim](http://doi.org/10.1016/j.neuroimage.2009.08.041) [age.2009.08.041](http://doi.org/10.1016/j.neuroimage.2009.08.041)
- Demiralp, T., Herrmann, C. S., Erdal, M. E., Ergenoglu, T., Keskin, Y. H., Ergen, M., & Beydagi, H. (2007). DRD4 and DAT1 polymorphisms modulate human gamma band responses. *Cerebral Cortex*, *17*(5), 1007–1019.
- Dietsch, G. (1932). Fourier-Analyse von Elektrencephalogrammen des Menschen. *Pflügers Archiv für die gesamte Physiologie des Menschen und der Tiere*, *230*, 106–112. [http://doi.org/](http://doi.org/10.1007/BF01751972) [10.1007/BF01751972](http://doi.org/10.1007/BF01751972)
- Dimigen, O., Valsecchi, M., Sommer, W., & Kliegl, R. (2009). Human microsaccade-related visual brain responses. *Journal of Neuroscience*, *29*(39), 12321–12331. [http://doi.org/10.1523/](http://doi.org/10.1523/JNEUROSCI.0911-09.2009) [JNEUROSCI.0911-09.2009](http://doi.org/10.1523/JNEUROSCI.0911-09.2009)
- Eckhorn, R., Bauer, R., Jordan, W., Brosch, M., Kruse, W., Munk, M., & Reitboeck, H. J. (1988). Coherent oscillations: A mechanism of feature linking in the visual cortex? *Biological Cybernetics*, *60*, 121–130.
- Elliott, M. A., Herrmann, C. S., Mecklinger, A., & Müller, H. J. (2000). The loci of oscillatory visual-object priming: A combined electroencephalographic and reaction-time study. *International Journal of Psychophysiology*, *38*(3), 225–241. [http://doi.org/10.1016/](http://doi.org/10.1016/S0167-8760(00)00167-7) [S0167-8760\(00\)00167-7](http://doi.org/10.1016/S0167-8760(00)00167-7)
- Engbert, R. (2006). Microsaccades: A microcosm for research on oculomotor control, attention, and visual perception. *Progress in Brain Research*, *154*, 177–192. [http://doi.org/](http://doi.org/10.1016/S0079-6123(06)54009-9) [10.1016/S0079-6123\(06\)54009-9](http://doi.org/10.1016/S0079-6123(06)54009-9)
- Engbert, R. & Kliegl, R. (2003). Microsaccades uncover the orientation of covert attention. *Vision Research*, *43*(9), 1035–1045. [http://doi.org/10.1016/S0042-6989\(03\)00084-1](http://doi.org/10.1016/S0042-6989(03)00084-1)
- Engel, A. K., Fries, P., & Singer, W. (2001). Dynamic predictions: oscillations and synchrony in top-down processing. *Nature Reviews Neuroscience*, *2*(10), 704–716. [http://doi.org/10.1038/](http://doi.org/10.1038/35094565) [35094565](http://doi.org/10.1038/35094565)
- Engel, A. K., Roelfsema, P. R., Fries, P., Brecht, M., & Singer, W. (1997). Role of the temporal domain for response selection and perceptual binding. *Cerebral Cortex*, *7*(6), 571–582. [http://](http://doi.org/10.1093/cercor/7.6.571) [doi.org/10.1093/cercor/7.6.571](http://doi.org/10.1093/cercor/7.6.571)
- Engel, A., König, P., Kreiter, A. K., & Singer, W. (1991). Interhemispheric synchronization of oscillatory neuronal responses in cat visual cortex. *Science*, *252*(5009), 1177–1179. [http://doi.](http://doi.org/10.1126/science.252.5009.1177) [org/10.1126/science.252.5009.1177](http://doi.org/10.1126/science.252.5009.1177)
- Enriquez-Geppert, S., Huster, R. J., & Herrmann, C. S. (2013). Boosting brain functions: Improving executive functions with behavioral training, neurostimulation, and
GAMMA ACTIVITY IN SENSORY AND COGNITIVE PROCESSING 169
- neurofeedback. *International Journal of Psychophysiology*, *88*(1), 1–16. [http://doi.org/10.1016/](http://doi.org/10.1016/j.ijpsycho.2013.02.001) [j.ijpsycho.2013.02.001](http://doi.org/10.1016/j.ijpsycho.2013.02.001)
- Fell, J. & Axmacher, N. (2011). The role of phase synchronization in memory processes. *Nature Reviews Neuroscience*, *12*(2), 105–118.
- Felleman, D. J. & Van Essen, D. C. (1991). Distributed hierarchical processing in the primate cerebral cortex. *Cerebral Cortex*, *1*, 1–47.
- Fitzgibbon, S. P., DeLosAngeles, D., Lewis, T. W., Powers, D. M., Whitham, E. M., Willoughby, J. O., & Pope, K. J. (2015). Surface Laplacian of scalp electrical signals and independent component analysis resolve EMG contamination of electroencephalogram. *International Journal of Psychophysiology*, *97*(3), 277–284.
- Freeman, W. J. (1975). *Mass action in the nervous system*. Academic Press.
- Freeman, W. J. & Skarda, C. A. (1985). Spatial EEG patterns, non-linear dynamics and perception: the neo-Sherringtonian view. *Brain Research Reviews*, *10*, 147–175.
- Frien, A., Eckhorn, R., Bauer, R., Woelbern, T., & Kehr, H. (1994). Stimulus-specific fast oscillations at zero phase between visual areas V1 and V2 of awake monkey. *Neuroreport*, *5*(17), 2273–2277.
- Fries, P. (2005). A mechanism for cognitive dynamics: Neuronal communication through neuronal coherence. *Trends in Cognitive Sciences*, *9*(10), 474–480. [http://doi.org/10.1016/](http://doi.org/10.1016/j.tics.2005.08.011) [j.tics.2005.08.011](http://doi.org/10.1016/j.tics.2005.08.011)
- Fries, P. (2009). Neuronal gamma-band synchronization as a fundamental process in cortical computation. *Annual Review of Neuroscience*, *32*(1), 209–224. [http://doi.org/10.1146/annu](http://doi.org/10.1146/annurev.neuro.051508.135603) [rev.neuro.051508.135603](http://doi.org/10.1146/annurev.neuro.051508.135603)
- Fries, P. (2015). Rhythms for cognition: Communication through coherence. *Neuron*, *88*(1), 220–235.
- Fries, P., Nikolić, D., & Singer, W. (2007). The gamma cycle. *Trends in Neurosciences*, *30*(7), 309–316.
- Fründ, I., Busch, N. A., Körner, U., Schadow, J., & Herrmann, C. S. (2007). EEG oscillations in the gamma and alpha range respond differently to spatial frequency. *Vision Research*, *47*(15), 2086–2098.
- Galambos, R., Makeig, S., & Talmachoff, P. J. (1981). A 40-Hz auditory potential recorded from the human scalp. *Proceedings of the National Academy of Sciences of the United States of America*, *78*(4), 2643–2647.
- Gallinat, J., Winterer, G., Herrmann, C. S., & Senkowski, D. (2004). Reduced oscillatory gamma-band responses in unmedicated schizophrenic patients indicate impaired frontal network processing. *Clinical Neurophysiology*, *115*(8), 1863–1874. [http://doi.org/10.1016/j.cli](http://doi.org/10.1016/j.clinph.2004.03.013) [nph.2004.03.013](http://doi.org/10.1016/j.clinph.2004.03.013)
- Goncharova, I. I., McFarland, D. J., Vaughan, T. M., & Wolpaw, J. R. (2003). EMG contamination of EEG: Spectral and topographical characteristics. *Clinical Neurophysiology*, *114*(9), 1580–1593.
- Gray, C. M., König, P., Engel, A. K., & Singer, W. (1989). Oscillatory responses in cat visual cortex exhibit inter-columnar synchronization which reflects global stimulus properties. *Nature*, *338*, 334–337.
- Gray, C. M. & Singer, W. (1989). Stimulus-specific neuronal oscillations in orientation columns of cat visual cortex. *Proceedings of the National Academy of Sciences of the United States of America*, *86*(5), 1698–1702.
- Gregoriou, G. G., Gotts, S. J., Zhou, H., & Desimone, R. (2009). High-frequency, long-range coupling between prefrontal and visual cortex during attention. *Science*, *324*(5931), 1207– 1210.
170 DANIEL STRÜBER and CHRISTOPH S. HERRMANN
- Gregoriou, G. G., Paneri, S., & Sapountzis, P. (2015). Oscillatory synchrony as a mechanism of attentional processing. *Brain Research*, *1626*, 165–182. [http://doi.org/10.1016/j.brain](http://doi.org/10.1016/j.brainres.2015.02.004) [res.2015.02.004](http://doi.org/10.1016/j.brainres.2015.02.004)
- Gruber, T., Maess, B., Trujillo-Barreto, N. J., & Müller, M. M. (2008). Sources of synchronized induced gamma-band responses during a simple object recognition task: A replication study in human MEG. *Brain Research*, *1196*, 74–84. [http://doi.org/10.1016/j.brain](http://doi.org/10.1016/j.brainres.2007.12.037) [res.2007.12.037](http://doi.org/10.1016/j.brainres.2007.12.037)
- Gruber, T., Müller, M. M., Keil, A., & Elbert, T. (1999). Selective visual-spatial attention induced gamma band responses in the human EEG. *Clinical Neurophysiology*, *110*(1999), 2074–2085.
- Gruber, T., Trujillo-Barreto, N. J., Giabbiconi, C. M., Valdés-Sosa, P. A., & Müller, M. M. (2006). Brain electrical tomography (BET) analysis of induced gamma band responses during a simple object recognition task. *NeuroImage*, *29*(3), 888–900. [http://doi.org/10.1016/](http://doi.org/10.1016/j.neuroimage.2005.09.004) [j.neuroimage.2005.09.004](http://doi.org/10.1016/j.neuroimage.2005.09.004)
- Gruber, T., Tsivilis, D., Montaldi, D., & Müller, M. M. (2004). Induced gamma band responses: An early marker of memory encoding and retrieval. *NeuroReport*, *15*(11), 1837– 1841.
- Haenschel, C., Bittner, R. A., Waltz, J., Haertling, F., Wibral, M., Singer, W., . . . Rodriguez, E. (2009). Cortical oscillatory activity is critical for working memory as revealed by deficits in early-onset schizophrenia. *Journal of Neuroscience*, *29*(30), 9481–9489. [http://doi.org/](http://doi.org/10.1523/JNEUROSCI.1428-09.2009) [10.1523/JNEUROSCI.1428-09.2009](http://doi.org/10.1523/JNEUROSCI.1428-09.2009)
- Hassler, U., Friese, U., Martens, U., Trujillo-Barreto, N., & Gruber, T. (2013). Repetition priming effects dissociate between miniature eye movements and induced gamma-band responses in the human electroencephalogram. *European Journal of Neuroscience*, *38*(3), 2425–2433.
- Hassler, U., Trujillo Barreto, N., & Gruber, T. (2011). Induced gamma band responses in human EEG after the control of miniature saccadic artifacts. *NeuroImage*, *57*(4), 1411–1421. [http://](http://doi.org/10.1016/j.neuroimage.2011.05.062) [doi.org/10.1016/j.neuroimage.2011.05.062](http://doi.org/10.1016/j.neuroimage.2011.05.062)
- Hermes, D., Miller, K. J., Wandell, B. A., & Winawer, J. (2015). Gamma oscillations in visual cortex: The stimulus matters. *Trends in Cognitive Sciences*, *19*(2), 57–58. [http://doi.org/](http://doi.org/10.1016/j.tics.2014.12.009) [10.1016/j.tics.2014.12.009](http://doi.org/10.1016/j.tics.2014.12.009)
- Herrmann, C. S. (2001). Human EEG responses to 1-100 Hz flicker: Resonance phenomena in visual cortex and their potential correlation to cognitive phenomena. *Experimental Brain Research*, *137*(3-4), 346–353.
- Herrmann, C. S. & Demiralp, T. (2005). Human EEG gamma oscillations in neuropsychiatric disorders. *Clinical Neurophysiology*, *116*(12), 2719–2733. [http://doi.org/10.1016/j.cli](http://doi.org/10.1016/j.clinph.2005.07.007) [nph.2005.07.007](http://doi.org/10.1016/j.clinph.2005.07.007)
- Herrmann, C. S., Fründ, I., & Lenz, D. (2010). Human gamma-band activity: A review on cognitive and behavioral correlates and network models. *Neuroscience and Biobehavioral Reviews*, *34*(7), 981–992.
- Herrmann, C. S., Lenz, D., Junge, S., Busch, N. A., & Maess, B. (2004). Memory-matches evoke human gamma-responses. *BMC Neuroscience*, *5*, 13.
- Herrmann, C. S. & Mecklinger, A. (2001). Gamma activity in human EEG is related to highspeed memory comparisons during object selective attention. *Visual Cognition*, *8*(3-5), 593–608.
- Herrmann, C. S., Mecklinger, A., & Pfeifer, E. (1999). Gamma responses and ERPs in a visual classification task. *Clinical Neurophysiology*, *110*(4), 636–642. [http://doi.org/10.1016/](http://doi.org/10.1016/S1388-2457(99)00002-4) [S1388-2457\(99\)00002-4](http://doi.org/10.1016/S1388-2457(99)00002-4)
GAMMA ACTIVITY IN SENSORY AND COGNITIVE PROCESSING 171
- Herrmann, C. S., Munk, M. H. J., & Engel, A. K. (2004). Cognitive functions of gamma-band activity: Memory match and utilization. *Trends in Cognitive Sciences*, *8*(8), 347–355. [http://](http://doi.org/10.1016/j.tics.2004.06.006) [doi.org/10.1016/j.tics.2004.06.006](http://doi.org/10.1016/j.tics.2004.06.006)
- Herrmann, C. S., Rach, S., Vosskuhl, J., & Strüber, D. (2014). Time-frequency analysis of eventrelated potentials: A brief tutorial. *Brain Topography*, *27*(4), 438–450. [http://doi.org/10.1007/](http://doi.org/10.1007/s10548-013-0327-5) [s10548-013-0327-5](http://doi.org/10.1007/s10548-013-0327-5)
- Herrmann, C. S. & Strüber, D. (2017). What can transcranial alternating current stimulation tell us about brain oscillations? *Current Behavioral Neuroscience Reports*, *4*(2), 128–137.
- Herrmann, C. S., Strüber, D., Helfrich, R. F., & Engel, A. K. (2016). EEG oscillations: From correlation to causality. *International Journal of Psychophysiology*, *103*, 12–21. [http://doi.org/](http://doi.org/10.1016/j.ijpsycho.2015.02.003) [10.1016/j.ijpsycho.2015.02.003](http://doi.org/10.1016/j.ijpsycho.2015.02.003)
- Iaccarino, H. F., Singer, A. C., Martorell, A. J., Rudenko, A., Gao, F., Gillingham, T. Z., . . . Tsai, L. H. (2016). Gamma frequency entrainment attenuates amyloid load and modifies microglia. *Nature*, *540*(7632), 230–235.
- Jadi, M. P., Behrens, M. M., & Sejnowski, T. J. (2016). Abnormal gamma oscillations in N-Methyl-D-Aspartate receptor hypofunction models of schizophrenia. *Biological Psychiatry*, *79*(9), 716–726.
- Janani, A. S., Grummett, T. S., Lewis, T. W., Fitzgibbon, S. P., Whitham, E. M., DelosAngeles, D., . . . Pope, K. J. (2018). Improved artefact removal from EEG using canonical correlation analysis and spectral slope. *Journal of Neuroscience Methods*, *298*, 1–15. [http://doi.org/](http://doi.org/10.1016/j.jneumeth.2018.01.004) [10.1016/j.jneumeth.2018.01.004](http://doi.org/10.1016/j.jneumeth.2018.01.004)
- Jasper, H. H. & Andrews, H. L. (1938). Electro-encephalography III. Normal differentiation of occipital and precentral regions in man. *Archives of Neurology & Psychiatry*, *39*(1), 96–115.
- Jensen, O., Kaiser, J., & Lachaux, J. P. (2007). Human gamma-frequency oscillations associated with attention and memory. *Trends in Neurosciences*, *30*(7), 317–324. [http://doi.org/10.1016/](http://doi.org/10.1016/j.tins.2007.05.001) [j.tins.2007.05.001](http://doi.org/10.1016/j.tins.2007.05.001)
- Kaiser, J. & Lutzenberger, W. (2005). Human gamma-band activity: A window to cognitive processing. *NeuroReport*, *16*(3), 207–211.
- Keizer, A. W., Verment, R. S., & Hommel, B. (2010). Enhancing cognitive control through neurofeedback: A role of gamma-band activity in managing episodic retrieval. *NeuroImage*, *49*(4), 3404–3413.
- Keizer, A. W., Verschoor, M., Verment, R. S., & Hommel, B. (2010). The effect of gamma enhancing neurofeedback on the control of feature bindings and intelligence measures. *International Journal of Psychophysiology*, *75*(1), 25–32. [http://doi.org/10.1016/j.ijpsy](http://doi.org/10.1016/j.ijpsycho.2009.10.011) [cho.2009.10.011](http://doi.org/10.1016/j.ijpsycho.2009.10.011)
- Keren, A. S., Yuval-Greenberg, S., & Deouell, L. Y. (2010). Saccadic spike potentials in gammaband EEG: Characterization, detection and suppression. *NeuroImage*, *49*(3), 2248–2263.
- Kopell, N., Ermentrout, G. B., Whittington, M. A., & Traub, R. D. (2000). Gamma rhythms and beta rhythms have different synchronization properties. *Proceedings of the National Academy of Sciences of the United States of America*, *97*(4), 1867–1872. [http://doi.org/10.1073/](http://doi.org/10.1073/pnas.97.4.1867) [pnas.97.4.1867](http://doi.org/10.1073/pnas.97.4.1867)
- Kreiter, A. K. & Singer, W. (1996). Stimulus-dependent synchronization of neuronal responses in the visual cortex of the awake macaque monkey. *Journal of Neuroscience*, *16*(7), 2381–2396.
- Lally, N., Mullins, P. G., Roberts, M. V., Price, D., Gruber, T., & Haenschel, C. (2014). Glutamatergic correlates of gamma-band oscillatory activity during cognition: A
172 DANIEL STRÜBER and CHRISTOPH S. HERRMANN
- concurrent ER-MRS and EEG study. *NeuroImage*, *85*, 823–833. [http://doi.org/10.1016/j.neu](http://doi.org/10.1016/j.neuroimage.2013.07.049) [roimage.2013.07.049](http://doi.org/10.1016/j.neuroimage.2013.07.049)
- Leicht, G., Kirsch, V., Giegling, I., Karch, S., Hantschk, I., Möller, H. J., . . . Mulert, C. (2010). Reduced early auditory evoked gamma-band response in patients with schizophrenia. *Biological Psychiatry*, *67*(3), 224–231.
- Lenz, D., Fischer, S., Schadow, J., Bogerts, B., & Herrmann, C. S. (2011). Altered evoked gammaband responses as a neurophysiological marker of schizophrenia? *International Journal of Psychophysiology*, *79*(1), 25–31.
- Lenz, D., Jeschke, M., Schadow, J., Naue, N., Ohl, F. W., & Herrmann, C. S. (2008). Human EEG very high frequency oscillations reflect the number of matches with a template in auditory short-term memory. *Brain Research*, *1220*, 81–92. [http://doi.org/10.1016/j.brain](http://doi.org/10.1016/j.brainres.2007.10.053) [res.2007.10.053](http://doi.org/10.1016/j.brainres.2007.10.053)
- Lenz, D., Krauel, K., Flechtner, H. H., Schadow, J., Hinrichs, H., & Herrmann, C. S. (2010). Altered evoked gamma-band responses reveal impaired early visual processing in ADHD children. *Neuropsychologia*, *48*(7), 1985–1993. [http://doi.org/10.1016/j.neuropsycholo](http://doi.org/10.1016/j.neuropsychologia.2010.03.019) [gia.2010.03.019](http://doi.org/10.1016/j.neuropsychologia.2010.03.019)
- Lenz, D., Krauel, K., Schadow, J., Baving, L., Duzel, E., & Herrmann, C. S. (2008). Enhanced gamma-band activity in ADHD patients lacks correlation with memory performance found in healthy children. *Brain Research*, *1235*, 117–132. [http://doi.org/10.1016/j.brain](http://doi.org/10.1016/j.brainres.2008.06.023) [res.2008.06.023](http://doi.org/10.1016/j.brainres.2008.06.023)
- Lutzenberger, W., Pulvermüller, F., Elbert, T., & Birbaumer, N. (1995). Visual stimulation alters local 40-Hz responses in humans: an EEG-study. *Neuroscience Letters*, *183*(1–2), 39–42. [http://doi.org/10.1016/0304-3940\(94\)11109-V](http://doi.org/10.1016/0304-3940(94)11109-V)
- Markov, N. T., Vezoli, J., Chameau, P., Falchier, A., Quilodran, R., Huissoud, C., . . . Kennedy, H. (2014). Anatomy of hierarchy: Feedforward and feedback pathways in macaque visual cortex. *Journal of Comparative Neurology*, *522*(1), 225–259.
- Martinez-Conde, S., Otero-Millan, J., & Macknik, S. L. (2013). The impact of microsaccades on vision: Towards a unified theory of saccadic function. *Nature Reviews Neuroscience*, *14*(2), 83–96.
- Mathes, B., Strüber, D., Stadler, M. A., & Başar-Eroǧlu, C. (2006). Voluntary control of Necker cube reversals modulates the EEG delta- and gamma-band response. *Neuroscience Letters*, *402*(1-2), 145–149.
- McNally, J. M. & McCarley, R. W. (2016). Gamma band oscillations: A key to understanding schizophrenia symptoms and neural circuit abnormalities. *Current Opinion in Psychiatry*, *29*(3), 202–210.
- Merkel, N., Wibral, M., Bland, G., & Singer, W. (2018). Endogenously generated gamma-band oscillations in early visual cortex: A neurofeedback study. *Human Brain Mapping*, *39*(9), 3487–3502.
- Merker, B. (2013). Cortical gamma oscillations: The functional key is activation, not cognition. *Neuroscience and Biobehavioral Reviews*, *37*(3), 401–417. [http://doi.org/10.1016/j.neubio](http://doi.org/10.1016/j.neubiorev.2013.01.013) [rev.2013.01.013](http://doi.org/10.1016/j.neubiorev.2013.01.013)
- Michalareas, G., Vezoli, J., van Pelt, S., Schoffelen, J. M., Kennedy, H., & Fries, P. (2016). Alphabeta and gamma rhythms subserve feedback and feedforward influences among human visual cortical areas. *Neuron*, *89*(2), 384–397.
- Miltner, W. H. R., Braun, C., Arnold, M., Witte, H., & Taub, E. (1999). Coherence of gammaband EEG activity as a basis for associative learning. *Nature*, *397*(6718), 434–436. [http://doi.](http://doi.org/10.1038/17126) [org/10.1038/17126](http://doi.org/10.1038/17126)
GAMMA ACTIVITY IN SENSORY AND COGNITIVE PROCESSING 173
- Minzenberg, M. J., Firl, A. J., Yoon, J. H., Gomes, G. C., Reinking, C., & Carter, C. S. (2010). Gamma oscillatory power is impaired during cognitive control independent of medication status in first-episode schizophrenia. *Neuropsychopharmacology*, *35*(13), 2590–2599. [http://](http://doi.org/10.1038/npp.2010.150) [doi.org/10.1038/npp.2010.150](http://doi.org/10.1038/npp.2010.150)
- Müller, M. M., Bosch, J., Elbert, T., Kreiter, A., Sosa, M., Sosa, P., & Rockstroh, B. (1996). Visually induced gamma-band responses in human electroencephalographic activity: A link to animal studies. *Experimental Brain Research*, *112*(1), 96–102. [http://doi.org/10.1007/](http://doi.org/10.1007/BF00227182) [BF00227182](http://doi.org/10.1007/BF00227182)
- Naue, N., Strüber, D., Fründ, I., Schadow, J., Lenz, D., Rach, S., Körner, U., & Herrmann, C. S. (2011). Gamma in motion: Pattern reversal elicits stronger gamma-band responses than motion. *NeuroImage*, *55*(2), 808–817.
- Nimmrich, V., Draguhn, A., & Axmacher, N. (2015). Neuronal network oscillations in neurodegenerative diseases. *Neuromolecular Medicine*, *17*(3), 270–284. [http://doi.org/](http://doi.org/10.1007/s12017-015-8355-9) [10.1007/s12017-015-8355-9](http://doi.org/10.1007/s12017-015-8355-9)
- Nottage, J. F. (2010). Uncovering gamma in visual tasks. *Brain Topography*, *23*(1), 58–71. [http://](http://doi.org/10.1007/s10548-009-0129-y) [doi.org/10.1007/s10548-009-0129-y](http://doi.org/10.1007/s10548-009-0129-y)
- Nottage, J. F. & Horder, J. (2016). State-of-the-art analysis of high-frequency (gamma range) electroencephalography in humans. *Neuropsychobiology*, *72*(3-4), 219–228. [http://doi.org/](http://doi.org/10.1159/000382023) [10.1159/000382023](http://doi.org/10.1159/000382023)
- Nottage, J. F., Morrison, P. D., Williams, S. C. R., & Ffytche, D. H. (2013). A novel method for reducing the effect of tonic muscle activity on the gamma band of the scalp EEG. *Brain Topography*, *26*(1), 50–61.
- Oppermann, F., Hassler, U., Jescheniak, J. D., & Gruber, T. (2012). The rapid extraction of gist early neural correlates of high-level visual processing. *Journal of Cognitive Neuroscience*, *24*(2), 521–529.
- Palop, J. J. & Mucke, L. (2016). Network abnormalities and interneuron dysfunction in Alzheimer disease. *Nature Reviews Neuroscience*, *17*(12), 777–792. [http://doi.org/10.1038/](http://doi.org/10.1038/nrn.2016.141) [nrn.2016.141](http://doi.org/10.1038/nrn.2016.141)
- Paulsen, O. & Sejnowski, T. J. (2000). Natural patterns of activity and long-term synaptic plasticity. *Current Opinion in Neurobiology*, *10*(2), 172–179. [http://doi.org/10.1016/](http://doi.org/10.1016/S0959-4388(00)00076-3) [S0959-4388\(00\)00076-3](http://doi.org/10.1016/S0959-4388(00)00076-3)
- Plöchl, M., Ossandón, J. P., & König, P. (2012). Combining EEG and eye tracking: Identification, characterization, and correction of eye movement artifacts in electroencephalographic data. *Frontiers in Human Neuroscience*, *6*, 278. [http://doi.org/](http://doi.org/10.3389/fnhum.2012.00278) [10.3389/fnhum.2012.00278](http://doi.org/10.3389/fnhum.2012.00278)
- Pope, K. J., Fitzgibbon, S. P., Lewis, T. W., Whitham, E. M., & Willoughby, J. O. (2009). Relation of gamma oscillations in scalp recordings to muscular activity. *Brain Topography*, *22*(1), 13– 17.
- Prehn-Kristensen, A., Wiesner, C. D., & Baving, L. (2015). Early gamma-band activity during interference predicts working memory distractibility in ADHD. *Journal of Attention Disorders*, *19*(11), 971–976.
- Pulvermüller, F., Birbaumer, N., Lutzenberger, W., & Mohr, B. (1997). High-frequency brain activity: Its possible role in attention, perception and language processing. *Progress in Neurobiology*, *52*(5), 427–445.
- Ray, S. & Maunsell, J. H. R. (2011). Different origins of gamma rhythm and high-gamma activity in macaque visual cortex. *PLoS Biology*, *9*(4), e1000610. [http://doi.org/10.1371/journal.](http://doi.org/10.1371/journal.pbio.1000610) [pbio.1000610](http://doi.org/10.1371/journal.pbio.1000610)
174 DANIEL STRÜBER and CHRISTOPH S. HERRMANN
- Ray, S. & Maunsell, J. H. R. (2015). Do gamma oscillations play a role in cerebral cortex? *Trends in Cognitive Sciences*, *19*(2), 78–85.
- Regan, D. (1968). A high frequency mechanism which underlies visual evoked potentials. *Electroencephalography and Clinical Neurophysiology*, *25*, 231–237.
- Regan, D. & Spekreijse, H. (1986). Evoked potentials in vision research 1961–86. *Vision Research*, *26*(9), 1461–1480.
- Reilly, T. J., Nottage, J. F., Studerus, E., Rutigliano, G., De Micheli, A. I., Fusar-Poli, P., & McGuire, P. (2018). Gamma band oscillations in the early phase of psychosis: A systematic review. *Neuroscience & Biobehavioral Reviews*, *90*, 381–399. [http://doi.org/10.1016/j.neubio](http://doi.org/10.1016/j.neubiorev.2018.04.006) [rev.2018.04.006](http://doi.org/10.1016/j.neubiorev.2018.04.006)
- Reva, N. V. & Aftanas, L. I. (2004). The coincidence between late non-phase-locked gamma synchronization response and saccadic eye movements. *International Journal of Psychophysiology*, *51*(3), 215–222.
- Rolfs, M., Kliegl, R., & Engbert, R. (2008). Toward a model of microsaccade generation: The case of microsaccadic inhibition. *Journal of Vision*, *8*(5), 1–23.
- Rossi, S., Hallett, M., Rossini, P. M., Pascual-Leone, A., Avanzini, G., Bestmann, S., . . . Ziemann, U. (2009). Safety, ethical considerations, and application guidelines for the use of transcranial magnetic stimulation in clinical practice and research. *Clinical Neurophysiology*, *120*(12), 2008–2039.
- Ruden, J. B., Dugan, L. L., Konradi, C. (2021). Parvalbumin interneuron vulnerability and brain disorders. *Neuropsychopharmacology*, 46, 279–287. [https://doi.org/10.1038/s41](https://doi.org/10.1038/s41386-020-0778-9) [386-020-0778-9](https://doi.org/10.1038/s41386-020-0778-9)
- Salari, N., Büchel, C., & Rose, M. (2014). Neurofeedback training of gamma band oscillations improves perceptual processing. *Experimental Brain Research*, *232*(10), 3353–3361. [http://doi.](http://doi.org/10.1007/s00221-014-4023-9) [org/10.1007/s00221-014-4023-9](http://doi.org/10.1007/s00221-014-4023-9)
- Salinas, E. & Sejnowski, T. J. (2001). Correlated neuronal activity and the flow of neural information. *Nature Reviews Neuroscience*, *2*, 539–550.
- Schadow, J., Lenz, D., Thaerig, S., Busch, N. A., Fründ, I., Rieger, J. W., & Herrmann, C. S. (2007). Stimulus intensity affects early sensory processing: Visual contrast modulates evoked gamma-band activity in human EEG. *International Journal of Psychophysiology*, *66*(1), 28–36.
- Schwartzman, D. J. & Kranczioch, C. (2011). In the blink of an eye: The contribution of microsaccadic activity to the induced gamma band response. *International Journal of Psychophysiology*, *79*(1), 73–82.
- Sejnowski, T. J. & Paulsen, O. (2006). Network oscillations: Emerging computational principles. *Journal of Neuroscience*, *26*(6), 1673–1676. [http://doi.org/10.1523/JNEURO](http://doi.org/10.1523/JNEUROSCI.3737-05d.2006) [SCI.3737-05d.2006](http://doi.org/10.1523/JNEUROSCI.3737-05d.2006)
- Senkowski, D. & Gallinat, J. (2015). Dysfunctional prefrontal gamma-band oscillations reflect working memory and other cognitive deficits in schizophrenia. *Biological Psychiatry*, *77*(12), 1010–1019.
- Sheer, D. E. (1984). Focused arousal, 40-Hz EEG, and dysfunction. In T. Elbert, B. Rockstroh, W. Lutzenberger, & N. Birbaumer (Eds.), *Self-regulation of the brain and behavior* (pp. 64– 84). Springer.
- Siegel, M., Donner, T. H., & Engel, A. K. (2012). Spectral fingerprints of large-scale neuronal interactions. *Nature Reviews Neuroscience*, *13*(2), 121–134.
- Singer, W. (2018). Neuronal oscillations: Unavoidable and useful? *European Journal of Neuroscience*, *48*(7), 2389–2398.
GAMMA ACTIVITY IN SENSORY AND COGNITIVE PROCESSING 175
- Singer, W. & Gray, C. M. (1995). Visual feature integration and the temporal correlation hypothesis. *Annual Review of Neuroscience*, *18*, 555–586. [http://doi.org/10.1146/annurev.](http://doi.org/10.1146/annurev.ne.18.030195.003011) [ne.18.030195.003011](http://doi.org/10.1146/annurev.ne.18.030195.003011)
- Spencer, K. M. (2012). Baseline gamma power during auditory steady-state stimulation in schizophrenia. *Frontiers in Human Neuroscience*, *5*, 190. [http://doi.org/10.3389/](http://doi.org/10.3389/fnhum.2011.00190) [fnhum.2011.00190](http://doi.org/10.3389/fnhum.2011.00190)
- Spencer, K. M., Niznikiewicz, M. A., Shenton, M. E., & McCarley, R. W. (2008). Sensoryevoked gamma oscillations in chronic schizophrenia. *Biological Psychiatry*, *63*(8), 744–747.
- Spydell, J. D., Ford, J. D., & Sheer, D. E. (1979). Task dependent cerebral lateralization of the 40 Hertz EEG rhythm. *Psychophysiology*, *16*(4), 347–350.
- Stroganova, T. A., Butorina, A. V., Sysoeva, O. V., Prokofyev, A. O., Nikolaeva, A. Y., Tsetlin, M. M., & Orekhova, E. V. (2015). Altered modulation of gamma oscillation frequency by speed of visual motion in children with autism spectrum disorders. *Journal of Neurodevelopmental Disorders*, *7*(1), 1–17.
- Strüber, D., Başar-Eroǧlu, C., Hoff, E., & Stadler, M. A. (2000). Reversal-rate dependent differences in the EEG gamma-band during multistable visual perception. *International Journal of Psychophysiology*, *38*(3), 243–252.
- Strüber, D., Başar-Eroǧlu, C., Miener, M., & Stadler, M. A. (2001). EEG gamma-band response during the perception of Necker cube reversals. *Visual Cognition*, *8*(3), 609–621. [http://doi.](http://doi.org/10.1080/13506280143000151) [org/10.1080/13506280143000151](http://doi.org/10.1080/13506280143000151)
- Strüber, D. & Herrmann, C. S. (2020). Modulation of gamma oscillations as a possible therapeutic tool for neuropsychiatric diseases: A review and perspective. *International Journal of Psychophysiology*, *152*, 15–25.
- Summerfield, C. & Mangels, J. A. (2006). Dissociable neural mechanisms for encoding predictable and unpredictable events. *Journal of Cognitive Neuroscience*, *18*(7), 1120–1132.
- Swettenham, J. B., Muthukumaraswamy, S. D., & Singh, K. D. (2009). Spectral properties of induced and evoked gamma oscillations in human early visual cortex to moving and stationary stimuli. *Journal of Neurophysiology*, *102*(2), 1241–1253. [http://doi.org/10.1152/](http://doi.org/10.1152/jn.91044.2008) [jn.91044.2008](http://doi.org/10.1152/jn.91044.2008)
- Tal, N. & Yuval-Greenberg, S. (2018). Reducing saccadic artifacts and confounds in brain imaging studies through experimental design. *Psychophysiology*, *55*(11), 1–20. [http://doi.org/](http://doi.org/10.1111/psyp.13215) [10.1111/psyp.13215](http://doi.org/10.1111/psyp.13215)
- Tallon-Baudry, C. (2009). The roles of gamma-band oscillatory synchrony in human visual cognition. *Frontiers in Bioscience*, *14*, 321–332.
- Tallon-Baudry, C. & Bertrand, O. (1999). Oscillatory gamma activity in humans and its role in object representation. *Trends in Cognitive Sciences*, *3*(4), 151–162.
- Tallon-Baudry, C., Bertrand, O., Delpuech, C., & Pernier, J. (1997). Oscillatory γ-band (30–70 Hz) activity induced by a visual search task in humans. *The Journal of Neuroscience*, *17*(2), 722–734.
- Tallon-Baudry, C., Bertrand, O., Delpuech, C., & Pernier, J. (1996). Stimulus specificity of phase-locked and non-phase-locked 40 Hz visual responses in human. *The Journal of Neuroscience*, *16*(13), 4240–4249.
- Tallon-Baudry, C., Bertrand, O., Peronnet, F., & Pernier, J. (1998). Induced gamma-band activity during the delay of a visual short-term memory task in humans. *The Journal of Neuroscience*, *18*(11), 4244–4254.
- Thickbroom, G. W. & Mastaglia, L. (1985). Presaccadic "spike" potential: Investigation of topography and source. *Brain Research*, *339*, 271–280.
176 DANIEL STRÜBER and CHRISTOPH S. HERRMANN
- Tombor, L., Kakuszi, B., Papp, S., Réthelyi, J., Bitter, I., & Czobor, P. (2019). Decreased resting gamma activity in adult attention deficit/hyperactivity disorder. *The World Journal of Biological Psychiatry, 20*(9), *691-702*.
- Uhlhaas, P. J. & Singer, W. (2006). Neural synchrony in brain disorders: Relevance for cognitive dysfunctions and pathophysiology. *Neuron*, *52*(1), 155–168. [http://doi.org/10.1016/j.neu](http://doi.org/10.1016/j.neuron.2006.09.020) [ron.2006.09.020](http://doi.org/10.1016/j.neuron.2006.09.020)
- Uhlhaas, P. J. & Singer, W. (2010). Abnormal neural oscillations and synchrony in schizophrenia. *Nature Reviews Neuroscience*, *11*(2), 100–113.
- Uhlhaas, P. J. & Singer, W. (2012). Neuronal dynamics and neuropsychiatric disorders: Toward a translational paradigm for dysfunctional large-scale networks. *Neuron*, *75*(6), 963–980.
- Valsecchi, M., Betta, E., & Turatto, M. (2007). Visual oddballs induce prolonged microsaccadic inhibition. *Experimental Brain Research*, *177*(2), 196–208. [http://doi.org/10.1007/s00](http://doi.org/10.1007/s00221-006-0665-6) [221-006-0665-6](http://doi.org/10.1007/s00221-006-0665-6)
- Valsecchi, M., Dimigen, O., Kliegl, R., Sommer, W., & Turatto, M. (2009). Microsaccadic inhibition and P300 enhancement in a visual oddball task. *Psychophysiology*, *46*(3), 635–644.
- Van Diessen, E., Senders, J., Jansen, F. E., Boersma, M., & Bruining, H. (2015). Increased power of resting-state gamma oscillations in autism spectrum disorder detected by routine electroencephalography. *European Archives of Psychiatry and Clinical Neuroscience*, *265*(6), 537– 540.
- Van Kerkoerle, T., Self, M. W., Dagnino, B., Gariel-Mathis, M.-A., Poort, J., van der Togt, C., & Roelfsema, P. R. (2014). Alpha and gamma oscillations characterize feedback and feedforward processing in monkey visual cortex. *Proceedings of the National Academy of Sciences of the United States of America*, *111*(40), 14332–14341.
- Varela, F., Lachaux, J. P., Rodriguez, E., & Martinerie, J. (2001). The brainweb: Phase synchronization and large-scale integration. *Nature Reviews Neuroscience*, *2*(4), 229–239. [http://doi.](http://doi.org/10.1038/35067550) [org/10.1038/35067550](http://doi.org/10.1038/35067550)
- Vinck, M. & Bosman, C. A. (2016). More gamma more predictions: Gamma-synchronization as a key mechanism for efficient integration of classical receptive field inputs with surround predictions. *Frontiers in Systems Neuroscience*, 10, 35.
- Von Stein, A., Chiang, C., & König, P. (2000). Top-down processing mediated by interareal synchronization. *Proceedings of the National Academy of Sciences of the United States of America*, *97*(26), 14748–14753.
- Von Stein, A. & Sarnthein, J. (2000). Different frequencies for different scales of cortical integration: From local gamma to long range alpha/theta synchronization. *International Journal of Psychophysiology*, *38*(3), 301–313. [http://doi.org/10.1016/S0167-8760\(00\)00172-0](http://doi.org/10.1016/S0167-8760(00)00172-0)
- Wang, J., Barstein, J., Ethridge, L. E., Mosconi, M. W., Takarae, Y., & Sweeney, J. A. (2013). Resting state EEG abnormalities in autism spectrum disorders. *Journal of Neurodevelopmental Disorders*, *5*(1), 24.
- Wang, X.-J. (2010). Neurophysiological and computational principles of cortical rhythms in cognition. *Physiological Reviews*, *90*(3), 1195–1268.
- White, R. S. & Siegel, S. J. (2016). Cellular and circuit models of increased resting-state network gamma activity in schizophrenia. *Neuroscience*, *321*, 66–76.
- Whitham, E. M., Lewis, T., Pope, K. J., Fitzgibbon, S. P., Clark, C. R., Loveless, S., . . . Willoughby, J. O. (2008). Thinking activates EMG in scalp electrical recordings. *Clinical Neurophysiology*, *119*(5), 1166–1175.
GAMMA ACTIVITY IN SENSORY AND COGNITIVE PROCESSING 177
- Whitham, E. M., Pope, K. J., Fitzgibbon, S. P., Lewis, T., Clark, C. R., Loveless, S., . . . Willoughby, J. O. (2007). Scalp electrical recording during paralysis: Quantitative evidence that EEG frequencies above 20 Hz are contaminated by EMG. *Clinical Neurophysiology*, *118*(8), 1877– 1888.
- Whittington, M. A., Cunningham, M. O., LeBeau, F. E. N., Racca, C., & Traub, R. D. (2011). Multiple origins of the cortical gamma rhythm. *Developmental Neurobiology*, *71*(1), 92–106.
- Whittington, M. A., Traub, R. D., Kopell, N., Ermentrout, B., & Buhl, E. H. (2000). Inhibitionbased rhythms: Experimental and mathematical observations on network dynamics. *International Journal of Psychophysiology*, *38*(3), 315–336.
- Yordanova, J., Banaschewski, T., Kolev, V., Woerner, W., & Rothenberger, A. (2001). Abnormal early stages of task stimulus processing in children with attention-deficit hyperactivity disorder: Evidence from event-related gamma oscillations. *Clinical Neurophysiology*, *112*(6), 1096–1108. [http://doi.org/10.1016/S1388-2457\(01\)00524-7](http://doi.org/10.1016/S1388-2457(01)00524-7)
- Yuval-Greenberg, S. & Deouell, L. Y. (2009). The broadband-transient induced gamma-band response in scalp EEG reflects the execution of saccades. *Brain Topography*, *22*(1), 3–6. [http://](http://doi.org/10.1007/s10548-009-0077-6) [doi.org/10.1007/s10548-009-0077-6](http://doi.org/10.1007/s10548-009-0077-6)
- Yuval-Greenberg, S., Tomer, O., Keren, A. S., Nelken, I., & Deouell, L. Y. (2008). Transient induced gamma-band response in EEG as a manifestation of miniature saccades. *Neuron*, *58*(3), 429–441.
- Zaehle, T., Fründ, I., Schadow, J., Thärig, S., Schoenfeld, M. A., & Herrmann, C. S. (2009). Inter- and intra-individual covariations of hemodynamic and oscillatory gamma responses in the human cortex. *Frontiers in Human Neuroscience*, *3*, 8. [http://doi.org/10.3389/](http://doi.org/10.3389/neuro.09.008.2009) [neuro.09.008.2009](http://doi.org/10.3389/neuro.09.008.2009)
## [CHAPTER 9](#page-6-1)
# [FRONTAL MIDLINE THETA](#page-6-1) [AS A MODEL SPECIMEN OF](#page-6-1) [CORTICAL THETA](#page-6-1)
JAMES F. CAVANAGH AND MICHAEL X COHEN
## **9.1 History**
Multiple distinct rhythmic processes in the approximate 4–8 Hz theta-band range have been historically observed in the continuous EEG. Widely distributed thetaband rhythmicity is commonly observed during stage 1 sleep. Abnormal background presence or hemispheric asymmetries in this rhythm are used to infer neural dysfunction in clinical practice. Yet nearly 70 years of observation have also detailed a taskrelated increase in frontal midline theta (FMT), usually observed over electrode Fz or its nearest 10/20 system neighbors during effortful mental processes (Arellano & Schwab, 1950; Brazier & Casby, 1952; Inouye, Shinosaki, Iyama, Matsumoto, Toi, et al., 1994; Sato, 1952). Since this FMT feature is cognitively induced, it has been considered distinct from arousal- or clinically related theta rhythms. These spatially specified and elicitationdependent distinctions are critical to make when describing any frequency-based EEG activity: manifest characteristics like a common frequency range can be shared between different latent processes.
Towards the end of the twentieth century, a growing quantitative approach to EEG was facilitated by advancements in signal processing methods, including event-related potentials (ERPs) and Fourier-based analyses, improvements in computational power to implement those analyses, and increased data quality through better scalp EEG equipment and direct intracranial human recordings during cognitive performance. Following these technical revolutions, an emerging consensus deduced that cortically generated theta-band activities are reliably associated with general cognitive performance (Başar, 1998b), including specific processes like working memory (Asada et al., 1999; Gevins et al., 1997; Ishii et al., 1999), spatial navigation (Kahana et al., 1999), or FRONTAL MIDLINE THETA AS A MODEL SPECIMEN OF CORTICAL THETA 179
episodic memory encoding and retrieval (Jacobs et al., 2006; Kahana et al., 1999; Klimesch, 1999; Klimesch et al., 2000; Nyhus & Curran, 2010; Rizzuto et al., 2006; Sauseng et al., 2004). These findings indicated that theta is generated across human neocortical areas (Caplan et al., 2003; Jacobs et al., 2006; Raghavachari et al., 2006) and that it reflects a multitude of active cortical processes. Here we reiterate our caveat for determining the relationship between a brain rhythm and a specific cognitive process: rhythmic processes reflect common neural operations that have distinct representational content depending on the generative neural system. Theta-band dynamics reflect a non-specific marker of active cortical operation. The frontal midline variant of theta is particularly prevalent in the human EEG, making it a good example for understanding broader cortical theta activities.
Experimental findings have accumulated an increasingly well-defined set of processes associated with FMT. Talairach and colleagues (1973) described how electrical stimulation of the human anterior cingulate cortex (ACC) elicited motor actions that were integrated with environmental context, sometimes accompanied by FMT oscillatory activities. Throughout the 1990s, the qualitative appearance of scalp-recorded FMT during cognitive effort could be reliably evoked (Asada et al., 1999; Inouye et al., 1994; Inouye, Shinosaki, Iyama, Matsumoto, Toi, et al., 1994) and a corresponding relationship with anxiety was often observed (Mizuki et al., 1997; Mizuki et al., 1992; Mizuki et al., 1996). These two *effective* and *affective* facets of vigilance have been increasingly associated with FMT throughout the past few decades. Paralleling the evolving capabilities of experimental neurophysiology, a growing area of research has moved beyond qualitative assessment towards a detailed quantification of the generators, elicitors, and moderators involved in the genesis of the FMT rhythm.
## **9.2 Characteristics**
Mental effort is a reliable elicitor of FMT (Smit et al., 2004; Smit et al., 2005). FMT increases during perseverance and decreases during fatigue (Wascher et al., 2014). Working memory load scales with FMT power (Gevins & Smith, 2000; Ishii et al., 1999; Itthipuripat et al., 2013; Onton et al., 2005; Sauseng et al., 2010), although it should be examined if this relationship is simply due to increased effort or if it represents specific information content (see Hsieh et al., 2011; Roberts et al., 2013). Memory encoding and retrieval are associated with broad cortical theta, including FMT (Hsieh & Ranganath, 2014; Jacobs et al., 2006; Kahana et al., 1999; Klimesch, 1999; Klimesch et al., 2000; Nyhus & Curran, 2010; Rizzuto et al., 2003, 2006; Sauseng et al., 2004). It remains unknown if the role of FMT is specific to control processes in memory rather than encoding per se (see Hanslmayr et al., 2010; Staudigl et al., 2010), particularly since other cortical theta is specifically associated with encoding (see Rizzuto et al., 2006; Wang et al., 2018).
FMT has been localized to broad medial frontal cortical areas, including the ACC and the midcingulate cortex (MCC) using MEG (Beaton et al., 2018; Ishii et al., 1999; Jensen 180 JAMES F. CAVANAGH and MICHAEL X COHEN
& Tesche, 2002) and EEG (Cohen & Ridderinkhof, 2013; Gevins & Smith, 2000; Gevins et al., 1999; Gevins et al., 1997; Onton et al., 2005). The MCC generates oscillations in the theta band in human intracranial recording (Cohen et al., 2008; Wang et al., 2005) as well as in non-human primates (Tsujimoto et al., 2010; Tsujimoto et al., 2006; Womelsdorf, Johnston, et al., 2010; Womelsdorf, Vinck, et al., 2010). Recent reviews have summarized distinct functional aspects of FMT, including its modulators (Mitchell, McNaughton, Flanagan, & Kirk, 2008), its role in memory (Hsieh & Ranganath, 2014), and its broader role in cognitive control (Cavanagh & Frank, 2014). We turn now to this defining area of cognitive control and the history of linking FMT processes to frontal midline ERP components intricately related to the need for control.
#### **9.2.1 ERP Findings Linked to the FMT Response**
Figure 9.1 shows frontal midline ERPs associated with a common theta-band substrate. The discovery of the response-locked frontal midline ERP feature known as the errorrelated negativity (ERN) indirectly motivated a renewed interest in FMT dynamics (Falkenstein et al., 1991; Gehring et al., 1993). Not long after its discovery, the ERN was characterized as being particularly sensitive to anxiety (Gehring et al., 2000) with a presumed generative source in ACC (Dehaene et al., 1994; Ishii et al., 1999; Van Veen & Carter, 2002). Importantly, the ERN was shown to have a spectral response in the theta band (Luu & Tucker, 2001; Luu et al., 2004), although concurrent delta-band activities have also been noted (Yordanova et al., 2004) and recently highlighted as functionally distinct processes (Cohen & Donner, 2013).
A smaller voltage negativity was also observed on non-error trials (Coles et al., 2001; Vidal et al., 2003; Vidal et al., 2000), which is sometimes called the correct-related negativity (CRN). While this EEG feature was sometimes interpreted as an artifact (Coles et al., 2001), it is now known to be reliably observed during action commission, even in the absence of task demands (Cavanagh et al., 2012). CRN amplitudes mirror variations in performance monitoring during manual responses, as they are larger under conditions of increased task difficulty (Hajcak et al., 2005) and uncertainty (Pailing & Segalowitz, 2004) and they are diminished on correct trials immediately preceding errors (Allain et al., 2004; Cavanagh et al., 2009).
A stimulus-locked error signal following punishing or error feedback was characterized soon after the discovery of the ERN (Miltner et al., 1997), with varied theoretical accounts arguing for a common process with the response-locked ERN (Holroyd & Coles, 2002; Holroyd et al., 2002) or a similar but distinct comparator process (Gehring & Willoughby, 2002). This component developed many different names, including the feedback-related negativity (FRN), the feedback error-related negativity (fERN), or the mediofrontal negativity (MFN). However, the process reflected by these terms all share common features with the well-known frontal midline N2 component (Folstein & Van Petten, 2008; Holroyd, 2002), arguing against any specificity of information content in these processes. Indeed, the N2 component was already known to
FRONTAL MIDLINE THETA AS A MODEL SPECIMEN OF CORTICAL THETA 181

**Figure 9.1** The need for cognitive control is associated with a similar frontal midline theta signature across a variety of eliciting events. (A) Phase-locked EEG activities (ERPs). While these ERP components (i.e., peaks and troughs in the signal locked to particular external events and averaged across trials) are related to learning and adaptive control, they represent a small fraction of ongoing neural dynamics. (B) Time-frequency plots show richer spectral dynamics of event-related neuro-electrical activity by averaging activities regardless of phase-locking. Here, significant increases in power to novelty, conflict, punishment, and error are outlined in black, revealing a common frontal midline theta band feature during events that signal a need for control. (C) Scalp topography of event-related frontal midline theta activity. The distribution of theta power bursts is consistently maximal over the frontal midline.
N2, a component elicited by novelty or stimulus/response conflict; Feedback related negativity (FRN), A similar N2-like component elicited by external feedback signaling that one's actions were incorrect or yielded a loss; Correct-related negativity (CRN), a small, obligatory component evoked by motor responses even when these are correct according to the task and enhanced by response conflict; Error related negativity (ERN), A component evoked by motor commission errors.
have a spectral representation in the theta band (Başar-Eroğlu et al., 1992; Başar, 1998a; Yordanova et al., 2002). The ERN and the FRN/N2 are estimated to have MCC sources via EEG source estimation (Gehring et al., 2012; Gruendler et al., 2011; van Noordt & Segalowitz, 2012; Walsh & Anderson, 2012) and EEG-informed fMRI (Becker et al., 2014; Debener et al., 2005; Edwards et al., 2012; Hauser et al., 2014; Huster et al., 2011), suggesting at least some common processes linking the two.
A parsimonious summary could propose that both the stimulus- and responserelated fronto-central negativities reflect common features of the processing demands of the MCC. These features are varied across systems related to cognitive and motor control, attention, and reinforcement learning, but are especially sensitive to mismatch signals of conflict, punishment, and error in the service of behavioral adaptation. The commonality of these theta-band processes led to an integrative theory of a common 182 JAMES F. CAVANAGH and MICHAEL X COHEN
language, a *theta lingua franca*, for the realization of the need for control (Cavanagh et al., 2009; 2012). Stimulus- and response-locked obligatory theta-band phase dynamics were proposed to represent a biophysical mechanism for the common temporal organization of neural processes during stimulus or response processes. Variation on this theme, such as power enhancement, reflects the realization of these reactive responses (Figure 9.1). These computations appear to be used to merge attentive, affective, and cognitive functions with motor selection in order to utilize environmental context during action monitoring. FMT therefore appears to reflect general operations of the MCC during action monitoring, particularly as an initial orienting response to a novel or surprising event (Wessel, 2018).
#### **9.2.2 Do ERP Theta and FMT Reflect the Same Process?**
Recent findings have begun to parse some of the overlapping constructs in the broad *theta lingua franca* perspective. FMT dynamics occur in the "background" during cognitive performance, emerging in a scale-free manner over varied time scales and thus not only to punctate evoked orienting responses (Cohen, 2016). Conflict appears to be specifically represented in the theta band, whereas error-specific features are associated with an additional delta-band response (Cohen & Donner, 2013; Cohen & van Gaal, 2014; Yordanova et al., 2004). Conflict can have many different definitions, with formal mathematical models equating to a type of surprise (Berlyne, 1957; Botvinick et al., 2001; Wiecki & Frank, 2013) and informal definitions comprising a homology of difficulty or effort.
In line with Shackman and colleagues' (2011) adaptive control hypothesis, FMT closely aligns with the proposed domain-general (effective and affective) role of the MCC for selecting actions under uncertainty (Cavanagh & Shackman, 2014). Metaanalytic evidence supports the hypothesis that cognitive effort and anxiety are both related to FMT and associated ERP features (Cavanagh & Shackman, 2014; Moser et al., 2013). Highly anxious individuals appear to utilize punishment and error information more effectively than a control sample. Enhanced FMT mediates the relationship between anxiety and risky decision making (Schmidt et al., 2018), and it correlates with an enhanced ability to learn from punishment (Cavanagh et al., 2018) and adjust behavior following errors (Cavanagh, Meyer, Hajcak, et al., 2017).
In sum, definitions of conflict, difficulty, and effort can all be equivalently applied to situations that elicit FMT as well as ERP components with theta-dominant substrates. In line with the adaptive control hypothesis, FMT appears to mediate the increased affective and effective vigilance leading to more avoidant behaviors, particularly in highly anxious individuals. However, our overarching caveat should be noted again: there are a multitude of theta band responses, even over the frontal midline, and each can reflect a variety of processes (Töllner et al., 2017). For example, Cohen and Donner (2013) found that the response-conflict-related N2 ERP component was uncorrelated with conflictrelated FMT, and that removing the phase-locked (ERP) component of the signal FRONTAL MIDLINE THETA AS A MODEL SPECIMEN OF CORTICAL THETA 183
did not affect the conflict-related FMT. This is consistent with other reports that have reported a qualitative absence of phase-locking associated with response-conflict FMT (Nigbur et al., 2012; Pastötter et al., 2010). These findings can be contrasted with similar analyses of the FMT response to erroneous button presses, which contains theta-band phase-locking (Trujillo & Allen, 2007) that is significantly affected by removing the ERP (Munneke et al., 2015).
## **9.3 Translational Underpinnings**
In some fields of neuroscience research, the term "theta" implicitly implies rodent hippocampal activity (~4–12 Hz) that has been associated with learning, memory, and spatial navigation (Buzsáki, 2006). Rodent hippocampal theta is not a unitary construct (Colgin, 2013; Pignatelli et al., 2012), with separate theta rhythms occurring due to septal drive as well as an intrinsic generative process that seems to be common to many types of cortical and sub-cortical excitatory-inhibitory networks (Womelsdorf et al., 2014).
Mediofrontal spikes are phase-locked to both mediofrontal theta as well as hippocampal theta (Benchenane et al., 2010; Hyman et al., 2011; Jones & Wilson, 2005b; 2005a; Paz et al., 2008; Pignatelli et al., 2012; Siapas et al., 2005). However, this evidence of hippocampal interaction with frontal theta processes could reflect a generic phenomenon whereby cortical theta synchronizes disparate neural areas in a global workspace, possibly via travelling waves (Lubenov & Siapas, 2009; Zhang et al., 2018). Many cortical areas have shown phase-synchronous relationships with frontal theta, including visual cortex (Lee et al., 2005; Liebe et al., 2012; Phillips et al., 2013), amygdala (Taub et al., 2018), and ventral tegmental areas (Fujisawa & Buzsáki, 2011). The ubiquity of thetaband findings across species has led to the suggestion that FMT reflects a non-specific mechanism for organizing neural processes around "decision points", such as action selection (Womelsdorf, Vinck, et al., 2010).
The translational potential for using theta to infer similar cognitive processes between species is promising but needs additional clarification. Some studies show that nonhuman primates have similar error, conflict, and feedback ERPs at the skull (Phillips & Everling, 2014), the scalp (Godlove et al., 2011), the dura (Vezoli & Procyk, 2009), and within the cingulate cortex (Emeric et al., 2010), although the spectral representation of these signals has not been defined. Rats have a FMT-dominant control network that is transiently instantiated following an imperative tone, affording a chance to causally manipulate this network and draw parallel conclusions to humans (Narayanan et al., 2013) although this is non-specifically spectrally localized to the theta band compared to typical human EEG findings. This common FMT electrophysiological response is diminished in Parkinson's patients as well as in a dopamine depletion rodent model (Parker et al., 2015), suggesting a novel model of cognitive dysfunction in Parkinsonism. Ample evidence suggests that FMT is sensitive to dopamine in humans, but it appears to also be sensitive to other monoamines like norepinephrine and acetylcholine (see 184 JAMES F. CAVANAGH and MICHAEL X COHEN
review by Jocham & Ullsperger, 2009) so the specificity of neuromodulator influence is likely to be low.
Given this pervasive dominance of theta-band activities across mammalian cognitive processes, one may wonder if there is something special about this frequency. Indeed, many mammalian motor activities occur within a broadly-defined theta frequency (Cohen, 2014; Colgin, 2013). Reflexive movements like sniffing (Macrides et al., 1982), whisking (Berg & Kleinfeld, 2002), licking (Amarante et al., 2017), giggling (Luschei, 2006), and shivering (Petajan & Williams, 1972), as well as controlled processes like saccade initiation (Jutras et al., 2013), typing (Yamaguchi et al., 2013), and speaking (Pellegrino et al., 2011), all occur with theta rhythmicity. This theta dominance of the speech rate may have emerged as a consequence of motor properties of mouth movements, which themselves emerged from reflexive sucking, chewing, and licking patterns (MacNeilage & Davis, 2001). Yet there are theta rhythms in attentive processes as well. Saccades reset hippocampal theta rhythms in monkeys (Jutras et al., 2013), which appear to facilitate the creation of grid-based representations of space (Killian et al., 2012). Sustained attention has rhythmic fluctuations at an approximate theta frequency (Helfrich et al., 2018; Huang et al., 2015), although this may be a general lowfrequency phenomenon and may not be specific to theta (VanRullen, 2016).
In sum, cognitive processes and controlled motor activities appear to emerge from existing phylogenetic scaffolds that use a basic pattern generator for action initiation. For whatever reason, theta rhythmicity may have first been leveraged to optimize skeleto-motor action integration. The common occurrence of theta across arousal, motor, cognitive, and attentive processes suggests a *degeneracy* of function: many different processes evoke a theta band correlate. Still, there might be a common computational advantage of particular temporal pattern.
## **9.3.1 Theta Phase Dynamics and Decision Integration**
Theta oscillatory dynamics are a possible computational mechanism by which expectations and outcomes can be compared. Oscillations alter the membrane potential of neurons "tuned" to the oscillation frequency, forcing windows of time where any given neuron is either more (trough) or less (peak) likely to be excited. Neurons participating in this given frequency perturbation are more likely to interact, exchange information, and modulate synaptic plasticity together (Fries, 2015). Since oscillations reflect the action of a fundamental, energy-efficient physical principle, functional dynamics of information processing may be inferred from the qualities inherent to oscillations: timing, prediction, storage, and communication.
The 1/f characteristic of brain oscillations suggests that small-amplitude fastoscillating networks are a characteristic of more local operations, whereas slow, large rhythms link areas over a greater spatial distance. Sinusoidal (harmonic) oscillators, such as the theta rhythm, are good time keepers due to the ability to predict future states based on knowledge of the oscillation period and the phase at any given moment FRONTAL MIDLINE THETA AS A MODEL SPECIMEN OF CORTICAL THETA 185
(Buzsáki, 2006). Pulsatile (non-harmonic, or relaxation) oscillators, such as the neuronal membrane potential, may be synchronized easily by harmonic oscillators which can act to separate information transfer and information intake (Buzsáki & Draguhn, 2004). These characteristics of timing and selective entrainment make oscillations a substrate for ongoing processing (storage) and phase reset (input enhancement), two necessary components of expectation and prediction (Buzsáki, 2006).
Across networks, oscillations within one network may entrain other neurons by locking them into the same oscillatory phase (Fries, 2005; Womelsdorf et al., 2007), to a harmonic oscillatory phase (Gruber et al., 2005), or by coupling a higher frequency power increase to lower frequency phase (Canolty et al., 2006; Jensen & Lisman, 2005). Coherent oscillations between distal areas are thought to reflect entrained inter-regional activity, which serves to increase the coordination of spike timing across spatially separate neural networks (Fries, 2005). Thus, slower oscillations like theta can act as a reader of fast activities (Buzsáki, 2010; Jensen & Colgin, 2007; Womelsdorf, Vinck, et al., 2010), for example integrating phonemes into words during speech processing (Giraud et al., 2007; Giraud & Poeppel, 2012). Theta phase thus appears to be a general neural mechanism for coupling disparate local gamma band sequences (Canolty & Knight, 2010; Fukai, 1999; Jensen & Lisman, 2005; Solomon et al., 2017; Tang et al., 2016; White et al., 2000). This pattern of theta-gamma coupling even forms the basis of some current network-level models of cognitive control (Gratton, 2018; Verguts, 2017).
### **9.3.2 Theta phase dynamics and cognitive control**
If FMT power bursts signal a generic need for control (Figure 9.1), theta-band phase synchrony between frontal midline and distal sites may communicate how to implement that control (Figure 9.2a). In the more than ten years since the initial publication of this simultaneous discovery by two separate groups (Cavanagh et al., 2009; Hanslmayr et al., 2008), there have been over 20 replications of this effect of transient similarity in theta-specific phase angle following a variety of events indicating a need for control. This finding further validates a theta-based similarity between conflict, punishment, error, and working-memory evoked FMT as a common *lingua franca* for implementing control.
Other types of statistical interaction have also been shown in theta-band networks, primarily using Granger prediction where midline areas lead distal areas (Cohen & van Gaal, 2013; Popov et al., 2018; Rajan et al., 2018; Zavala et al., 2016; Zavala et al., 2014). Intracranial recordings in humans have validated the hypothesis that cingulate theta couples with gamma, and that this process leads dlPFC, MFC, and OFC during the need for cognitive control (Bartoli et al., 2017; Oehrn et al., 2014; Rothé et al., 2011; Smith et al., 2015; Tang et al., 2016). Similar medio-occipital phase synchrony has been observed in monkeys (Phillips et al., 2013) and medio-motor synchrony has been observed in rats (Narayanan et al., 2013). These theta-phase networks can be boosted by transcranial stimulation (Reinhart & Woodman, 2014; Reinhart, 2017), and diminished
186 JAMES F. CAVANAGH and MICHAEL X COHEN

**Figure 9.2** Theta band phase consistency between mid-frontal and distal sites is transiently increased following events that indicate a need for control. (A) Twenty five separate studies (A through Y) have replicated the finding of theta-band phase synchrony between the frontal midline (presumably MCC) and varied cortical areas, including lateral prefrontal cortex (lPFC), motor cortex, sensory cortices, and basal ganglia (BG). WM = working memory. (B) A variety of moderators affect medio-lateral phase synchrony, with increases due to age, anxiety and transcranial direct or alternating current stimulation (tD/ACS), and decreases due to schizophrenia, age, anti-phase tACS, and mild traumatic brain injury (TBI). (C) Studies oftentimes report a nominal pattern of hemisphericity in medio-lateral phase synchrony. Errors and punishments consistently evoked a right>left pattern, whereas conflict tended towards a left>right pattern. However, the studies contributing to the left>right pattern were more complex and involved proactive and reactive processes compared to error realization, which is rather straightforward and reactive. Future studies should formally investigate the moderators of hemisphericity in medio-lateral phase synchrony.
Citations for figure 9.2:
A: Hanslmayr et al., 2008; B: Cavanagh et al., 2009; C: Cohen et al., 2009; D: Cavanagh et al., 2010; E: Cohen & Cavanagh, 2011; F: Cohen & van Gaal, 2013; G: Nigbur et al., 2012; H: van de Vijver et al., 2011; I: van Driel et al., 2012; J: Narayanan et al., 2013; K: Anguera et al., 2013; L: Cohen & van Gaal, 2014; M: Tóth et al., 2014; N: Van de Vijver et al., 2014; O: Moran et al., 2014; P: Reinhart et al., 2015; Q: Zavala et al., 2013; R: Cavanagh et al., 2017; S: Reinhart, 2017; T: Vissers et al., 2018: U: Ryman et al., 2018; V: Swart et al., 2018; W: Buzzell et al., 2018; X: Oehrn et al., 2014; Y: Cavanagh et al., 2020.
FRONTAL MIDLINE THETA AS A MODEL SPECIMEN OF CORTICAL THETA 187
by out-of-phase alternating current (Reinhart, 2017). These networks are also altered in psychiatric distress, being increased in anxiety (Cavanagh et al., 2017) and diminished in schizophrenia (Ryman et al., 2018), see Figure 9.2b. Many questions remain to be addressed about the function of this theta-band phase synchrony, but there is correlative (Anguera et al., 2013; Cavanagh et al., 2009; Cavanagh et al., 2017; Swart et al., 2018) and causal evidence (Narayanan et al., 2013; Reinhart, 2017; Reinhart et al., 2015) that this network directly affects behaviors related to the ability to learn from and adapt to the need for control.
Many studies have observed a right-sided dominance of medio-lateral phase synchrony, but this issue of hemisphericity requires further rigorous testing. Figure 9.2c sorts studies that reported even a nominal pattern of hemisphericity, and it can be seen that errors and punishments consistently evoked a right>left bias, whereas conflict tended towards a left>right bias. Although this distinction appears straightforward, it is likely overly simplistic to suggest a simple conflict vs. error dissociation on hemisphericity. The studies contributing to the left>right pattern were more complex and involved both proactive and reactive processes whereas error realization is rather straightforward and reactive. Future studies should be formally test for hemispheric bias in medio-lateral phase synchrony to better address questions about the functional role of this signal.
## **9.4 Clinical applications**
FMT and related ERP features have compelling characteristics for clinical advancement. The majority of the units of analysis in the National Institute of Mental Health (NIMH) Research Domain Criteria (Insel et al., 2010) are EEG-based, and many of these are FMT-family responses. Lower FMT appears to be a reliable endophenotype for substance abuse and externalizing disorders (Gilmore et al., 2010; Kamarajan et al., 2015; Kang et al., 2012; Rangaswamy et al., 2007; Zlojutro et al., 2011). Higher FMT is reliably associated with anxious temperament (Cavanagh & Shackman, 2014; Moser et al., 2013; Riesel et al., 2017), and ERN amplitude can even predict treatment response in anxiety disorder patients (Gorka et al., 2018) . Future studies should derive the sensitivity and specificity of FMT to determine the biomarker potential in select clinical applications.
FMT can be elicited in simple tasks that are viable within a clinical environment. Aberrant auditory orienting responses have already been advanced as candidate biomarkers, like diminished mismatch negativity (MMN) in schizophrenia (Javitt et al., 2018; Light et al., 2015) or diminished novelty habituation in Parkinson's disease (Cavanagh, Kumar, et al., 2018). The MMN is a theta-dominant response with separable frontal and temporal processes (Fuentemilla et al., 2008; Ko et al., 2012) that may interact via theta-band phase synchrony (Choi et al., 2013). The neural systems underlying auditory novelty detection are well detailed in rodent models (Escera & 188 JAMES F. CAVANAGH and MICHAEL X COHEN
Malmierca, 2014; Featherstone et al., 2018; Lee et al., 2018), facilitating cross-species translation. Auditory-evoked responses are already routinely used in brainstem auditory testing for hearing acuity in newborns, demonstrating that clinical infrastructure and expertise exists for applying relevant tasks to patient groups when using EEG as a diagnostic tool.
# **9.5 Broader impact and future directions**
FMT is a well-characterized candidate mechanism underlying the ability to realize and communicate the need for cognitive control. Further tests of this theory will need to integrate findings from preclinical animal models, computational accounts of information representation, broader human imaging literature, and the sensitivity and specificity diagnostics for human patient groups. Fortunately, electrophysiology is routinely utilized in vitro, in vivo, and in outpatient neurological clinics, making it uniquely positioned at the crossroads of many sub-fields of neuroscience.
#### **References**
- Allain, S., Carbonnell, L., Falkenstein, M., Burle, B., & Vidal, F. (2004). The modulation of the Ne-like wave on correct responses foreshadows errors. *Neuroscience Letters*, *372*(1–2), 161– 166. [https://doi.org/S0304-3940\(04\)01171-1 \[pii\]10.1016/j.neulet.2004.09.036](https://doi.org/S0304-3940(04)01171-1%20[pii]10.1016/j.neulet.2004.09.036)
- Amarante, L. M., Caetano, M. S., & Laubach, M. (2017). Medial frontal theta is entrained to rewarded actions. *The Journal of Neuroscience*, *37*(44), 1965–1917. [https://doi.org/10.1523/](https://doi.org/10.1523/JNEUROSCI.1965-17.2017) [JNEUROSCI.1965-17.2017](https://doi.org/10.1523/JNEUROSCI.1965-17.2017)
- Anguera, J. A., Boccanfuso, J., Rintoul, J. L., Al-Hashimi, O., Faraji, F., Janowich, J., . . . Gazzaley, A. (2013). Video game training enhances cognitive control in older adults. *Nature*, *501*(7465), 97–101.
- Arellano, A. P. & Schwab, R. S. (1950). Scalp and basal recording during mental activity. Proceedings of the 1st International Congress of Psychiatry, September 18–27, Paris.
- Asada, H., Fukuda, Y., Tsunoda, S., Yamaguchi, M., & Tonoike, M. (1999). Frontal midline theta rhythms reflect alternative activation of prefrontal cortex and anterior cingulate cortex in humans. *Neuroscience Letters*, *274*(1), 29–32. [https://doi.org/S0304-3940\(99\)00679-5](https://doi.org/S0304-3940(99)00679-5)
- Bartoli, E., Conner, C. R., Kadipasaoglu, C. M., Yellapantula, S., Rollo, M. J., Carter, C. S., & Tandon, N. (2017). Temporal dynamics of human frontal and cingulate neural activity during conflict and cognitive control. *Cerebral Cortex*, *28*(11), 3842–3856. [https://doi.org/](https://doi.org/10.1093/cercor/bhx245) [10.1093/cercor/bhx245](https://doi.org/10.1093/cercor/bhx245)
- Başar-Eroğlu, C., Başar, E., Demiralp, T., & Schurmann, M. (1992). P300-response: Possible psychophysiological correlates in delta and theta frequency channels. A review. *International Journal of Psychophysiology*, *13*, 161–179.
- Başar, E. (1998a). Brain function and oscillations: Brain oscillations–principles and approaches. Springer-Verlag.
FRONTAL MIDLINE THETA AS A MODEL SPECIMEN OF CORTICAL THETA 189
- Başar, E. (1998b). Brain function and oscillations: Integrative brain function–neurophysiology and cognitive processes. Springer-Verlag.
- Beaton, L. E., Azma, S., & Marinkovic, K. (2018). When the brain changes its mind: Oscillatory dynamics of conflict processing and response switching in a flanker task during alcohol challenge. *PLoS One*, *13*(1), 1–24.
- Becker, M. P. I., Nitsch, A. M., Miltner, W. H. R., & Straube, T. (2014). A single-trial estimation of the feedback-related negativity and its relation to BOLD responses in a time-estimation task. *The Journal of Neuroscience*, *34*(8), 3005–3012. [https://doi.org/10.1523/JNEURO](https://doi.org/10.1523/JNEUROSCI.3684-13.2014) [SCI.3684-13.2014](https://doi.org/10.1523/JNEUROSCI.3684-13.2014)
- Benchenane, K., Peyrache, A., Khamassi, M., Tierney, P. L., Gioanni, Y., Battaglia, F. P., & Wiener, S. I. (2010). Coherent theta oscillations and reorganization of spike timing in the hippocampal-prefrontal network upon learning. *Neuron*, *66*(6), 921–936. [https://doi.org/](https://doi.org/10.1016/j.neuron.2010.05.013) [10.1016/j.neuron.2010.05.013](https://doi.org/10.1016/j.neuron.2010.05.013)
- Berg, R. W. & Kleinfeld, D. (2002). Rhythmic whisking by rat: Retraction as well as protraction of the vibrissae is under active muscular control. *Journal of Neurophysiology*, *89*(1), 104–117.
- Berlyne, D. E. (1957). Uncertainty and conflict: A point of contact between information-theory and behavior-theory concepts. *Psychological Review*, *64*(6), 329–339.
- Botvinick, M. M., Braver, T. S., Barch, D. M., Carter, C. S., & Cohen, J. D. (2001). Conflict monitoring and cognitive control. *Psychological Review*, *108*(3), 624–652. [https://pubmed.](https://pubmed.ncbi.nlm.nih.gov/11488380/) [ncbi.nlm.nih.gov/11488380/](https://pubmed.ncbi.nlm.nih.gov/11488380/)
- Brazier, M. A. B. & Casby, J. U. (1952). Cross-correlation and autocorrelation studies of electroencephalographic potentials. *Electroencephalography and Clinical Neurophysiology*, *4*, 201–211.
- Buzsáki, G. (2006). Rhythms of the brain. Oxford University Press.
- Buzsáki, G. (2010). Neural syntax: Cell assemblies, synapsembles, and readers. *Neuron*, *68*(3), 362–385.
- Buzsáki, G. & Draguhn, A. (2004). Neuronal oscillations in cortical networks. *Science*, *304*(5679), 1926–1929. [https://doi.org/10.1126/science.1099745 304/5679/1926](https://doi.org/10.1126/science.1099745%20304/5679/1926)
- Buzzell, G. A., Barker, T. V, Troller-Renfree, S. V, Bernat, E. M., Bowers, M. E., Morales, S., . . . Fox, N. A. (2018). Adolescent cognitive control, theta oscillations, and social motivation. *BioRxiv* [online], 366831.
- Canolty, R. T., Edwards, E., Dalal, S. S., Soltani, M., Nagarajan, S. S., Kirsch, H. E., . . . Knight, R. T. (2006). High gamma power is phase-locked to theta oscillations in human neocortex. *Science*, *313*(5793), 1626–1628.
- Canolty, R. T. & Knight, R. T. (2010). The functional role of cross-frequency coupling. *Trends in Cognitive Sciences*, *14*(11), 506–515.
- Caplan, J. B., Madsen, J. R., Schulze-Bonhage, A., Aschenbrenner-Scheibe, R., Newman, E. L., & Kahana, M. J. (2003). Human theta oscillations related to sensorimotor integration and spatial learning. *Journal of Neuroscience*, *23*(11), 4726–4736.
- Cavanagh, J. F., Bismark, A. W., Frank, M. J., & Allen, J. J. B. (2018). Multiple dissociations between comorbid depression and anxiety on reward and punishment processing: Evidence from computationally informed EEG. *Computational Psychiatry*, *3*, 1–17. [doi: 10.1162/cpsy\\_a\\_00024.](http://doi:%2010.1162/cpsy_a_00024%22)
- Cavanagh, J. F., Cohen, M. X., & Allen, J. J. B. (2009). Prelude to and resolution of an error: EEG phase synchrony reveals cognitive control dynamics during action monitoring. *The Journal of Neuroscience*, *29*(1), 98–105.
190 JAMES F. CAVANAGH and MICHAEL X COHEN
- Cavanagh, J. F. & Frank, M. J. (2014). Frontal theta as a mechanism for cognitive control. *Trends in Cognitive Sciences*, *18*(8), 1–8.
- Cavanagh, J. F., Frank, M. J., Klein, T. J., & Allen, J. J. B. (2010). Frontal theta links prediction errors to behavioral adaptation in reinforcement learning. *NeuroImage*, *49*(4), 3198–3209.
- Cavanagh, J. F., Kumar, P., Mueller, A. A., Pirio Richardson, S., Mueen, A., & Richardson, S. P. (2018). Diminished EEG habituation to novel events effectively classifies Parkinson's patients. *Clinical Neurophysiology*, *129*(2), 409–418.
- Cavanagh, J. F., Meyer, A., & Hajcak, G. (2017). Error-specific cognitive control alterations in generalized anxiety disorder. *Biological Psychiatry: Cognitive Neuroscience and Neuroimaging*, *2*(5), 413–420.
- Cavanagh, J. F., Rieger, R. E., Wilson, J. K., Gill, D., Fullerton, L., Brandt, E., & Mayer, A. R. (2020). Joint analysis of frontal theta synchrony and white matter following mild traumatic brain injury. *Brain Imaging and Behavior*, *14*(6), 2210–2223.
- Cavanagh, J. F., & Shackman, A. J. (2014). Frontal midline theta reflects anxiety and cognitive control: Meta-analytic evidence. *Journal of Physiology*, *109*(1–3), 3–15. [https://doi.org/](https://doi.org/10.1016/j.jphysparis.2014.04.003) [10.1016/j.jphysparis.2014.04.003](https://doi.org/10.1016/j.jphysparis.2014.04.003)
- Cavanagh, J. F., Zambrano-Vazquez, L., & Allen, J. J. B. (2012). Theta lingua franca: A common mid-frontal substrate for action monitoring processes. *Psychophysiology*, *49*(2), 220–238.
- Choi, J. W., Lee, J. K., Ko, D., Lee, G. T., Jung, K. Y., & Kim, K. H. (2013). Fronto-temporal interactions in the theta-band during auditory deviant processing. *Neuroscience Letters*, *548*, 120–125.
- Cohen, M. X. (2014). A neural microcircuit for cognitive conflict detection and signaling. *Trends in Neurosciences*, *37*(9), 480–490.
- Cohen, M. X. (2016). Midfrontal theta tracks action monitoring over multiple interactive time scales. *NeuroImage*, *141*, 262–272.
- Cohen, M. X. & Cavanagh, J. F. (2011). Single-trial regression elucidates the role of prefrontal theta oscillations in response conflict. *Frontiers in Psychology* [online], *2*, 30. [https://doi.org/](https://doi.org/10.3389/fpsyg.2011.00030) [10.3389/fpsyg.2011.00030](https://doi.org/10.3389/fpsyg.2011.00030)
- Cohen, M. X. & Donner, T. H. (2013). Midfrontal conflict-related theta-band power reflects neural oscillations that predict behavior. *Journal of Neurophysiology*, *110*(12), 2752–2763.
- Cohen, M. X. & Ridderinkhof, K. R. (2013). EEG source reconstruction reveals frontal-parietal dynamics of spatial conflict processing. *PLoS One*, *8*(2), e57293. [https://doi.org/10.1371/jour](https://doi.org/10.1371/journal.pone.0057293) [nal.pone.0057293](https://doi.org/10.1371/journal.pone.0057293)
- Cohen, M. X., Ridderinkhof, K. R., Haupt, S., Elger, C. E., & Fell, J. (2008). Medial frontal cortex and response conflict: Evidence from human intracranial EEG and medial frontal cortex lesion. *Brain Research*, *1238*, 127–142. [https://doi.org/S0006-8993\(08\)01872-6 \[pii\]10.1016/](https://doi.org/S0006-8993(08)01872-6%20[pii]10.1016/j.brainres.2008.07.114) [j.brainres.2008.07.114](https://doi.org/S0006-8993(08)01872-6%20[pii]10.1016/j.brainres.2008.07.114)
- Cohen, M. X, & van Gaal, S. (2013). Dynamic interactions between large-scale brain networks predict behavioral adaptation after perceptual errors. *Cerebral Cortex (New York, N.Y.: 1991)*, *23*(5), 1061–1072.
- Cohen, M. X, & van Gaal, S. (2014). Subthreshold muscle twitches dissociate oscillatory neural signatures of conflicts from errors. *NeuroImage*, *86*, 503–513. [https://doi.org/10.1016/J.NEU](https://doi.org/10.1016/J.NEUROIMAGE.2013.10.033) [ROIMAGE.2013.10.033](https://doi.org/10.1016/J.NEUROIMAGE.2013.10.033)
FRONTAL MIDLINE THETA AS A MODEL SPECIMEN OF CORTICAL THETA 191
- Cohen, M. X, van Gaal, S., Ridderinkhof, K. R., & Lamme, V. A. F. (2009). Unconscious errors enhance prefrontal-occipital oscillatory synchrony. *Frontiers in Human Neuroscience*, *3*, 54.
- Coles, M. G., Scheffers, M. K., & Holroyd, C. B. (2001). Why is there an ERN/Ne on correct trials? Response representations, stimulus-related components, and the theory of error-processing. *Biological Psychology*, *56*(3), 173–189. [https://doi.org/10.1016/S0301-0511\(01\)00076-X](https://doi.org/10.1016/S0301-0511(01)00076-X)
- Colgin, L. L. (2013). Mechanisms and functions of theta rhythms. *Annual Review of Neuroscience*, *36*(1), 295–312.
- Debener, S., Ullsperger, M., Siegel, M., Fiehler, K., von Cramon, D. Y., & Engel, A. K. (2005). Trial-by-trial coupling of concurrent electroencephalogram and functional magnetic resonance imaging identifies the dynamics of performance monitoring. *Journal of Neuroscience*, *25*(50), 11730–11737.[pii]10.1523/JNEUROSCI.3286-05.2005
- Dehaene, S., Posner, M. I., & Tucker, D. M. (1994). Localization of a neural system for error detection and compensation. *Psychological Science*, *5*(5),303–305.
- Edwards, B. G., Calhoun, V. D., & Kiehl, K. A. (2012). Joint ICA of ERP and fMRI during error-monitoring. *NeuroImage*, *59*(2), 1896–1903. [https://doi.org/10.1016/j.neuroim](https://doi.org/10.1016/j.neuroimage.2011.08.088) [age.2011.08.088](https://doi.org/10.1016/j.neuroimage.2011.08.088)
- Emeric, E. E., Leslie, M. W., Pouget, P., & Schall, J. D. (2010). Performance monitoring local field potentials in the medial frontal cortex of primates: Supplementary eye field. *Journal of Neurophysiology*, *104*, 1523–1537.
- Escera, C. & Malmierca, M. S. (2014). The auditory novelty system: An attempt to integrate human and animal research. *Psychophysiology*, *51*(2), 111–123. [https://doi.org/10.1111/](https://doi.org/10.1111/psyp.12156) [psyp.12156](https://doi.org/10.1111/psyp.12156)
- Falkenstein, M., Hohnsbein, J., Hoormann, J., & Blanke, L. (1991). Effects of crossmodal divided attention on late ERP components. II. Error processing in choice reaction tasks. *Electroencephalography and Clinical Neurophysiology*, *78*(6), 447–455. https://pubmed.ncbi. nlm.nih.gov/1712280/
- Featherstone, R. E., Melnychenko, O., & Siegel, S. J. (2018). Mismatch negativity in preclinical models of schizophrenia. *Schizophrenia Research*, *191*, 35–42. [https://doi.org/10.1016/j.sch](https://doi.org/10.1016/j.schres.2017.07.039) [res.2017.07.039](https://doi.org/10.1016/j.schres.2017.07.039)
- Folstein, J. R. & Van Petten, C. (2008). Influence of cognitive control and mismatch on the N2 component of the ERP: a review. *Psychophysiology*, *45*(1), 152–170. [pii]10.1111/j.1469-8986.2007.00602.x
- Fries, P. (2005). A mechanism for cognitive dynamics: neuronal communication through neuronal coherence. *Trends in Cognitive Science*, *9*(10), 474–480. [https://doi.org/S1364-](https://doi.org/S1364-6613(05)00242-1%20[pii]10.1016/j.tics.2005.08.011) [6613\(05\)00242-1 \[pii\]10.1016/j.tics.2005.08.011](https://doi.org/S1364-6613(05)00242-1%20[pii]10.1016/j.tics.2005.08.011)
- Fries, P. (2015). Rhythms for cognition: Communication through coherence. *Neuron*, *88*(1), 220–235.
- Fuentemilla, L., Marco-Pallarés, J., Münte, T. F., & Grau, C. (2008). Theta EEG oscillatory activity and auditory change detection. *Brain Research*, *1220*, 93–101. [https://doi.org/10.1016/](https://doi.org/10.1016/j.brainres.2007.07.079) [j.brainres.2007.07.079](https://doi.org/10.1016/j.brainres.2007.07.079)
- Fujisawa, S. & Buzsáki, G. (2011). A 4 Hz oscillation adaptively synchronizes prefrontal, VTA, and hippocampal activities. *Neuron*, *72*(1), 153–165. [https://doi.org/10.1016/j.neu](https://doi.org/10.1016/j.neuron.2011.08.018) [ron.2011.08.018](https://doi.org/10.1016/j.neuron.2011.08.018)
- Fukai, T. (1999). Sequence generation in arbitrary temporal patterns from theta-nested gamma oscillations: A model of the basal ganglia-thalamo-cortical loops. *Neural Networks*, *12*(7–8), 975–987. https://pubmed.ncbi.nlm.nih.gov/12662640/
192 JAMES F. CAVANAGH and MICHAEL X COHEN
- Gehring, W. J., Goss, B., Coles, M. G. H., Meyer, D. E., & Donchin, E. (1993). A neural system for error-detection and compensation. *Psychological Science*, *4*(6), 385–390.
- Gehring, W. J., Himle, J., & Nisenson, L. G. (2000). Action-monitoring dysfunction in obsessive-compulsive disorder. *Psychological Science*, *11*(1), 1–6. [https://pubmed.ncbi.nlm.](https://pubmed.ncbi.nlm.nih.gov/11228836/) [nih.gov/11228836/](https://pubmed.ncbi.nlm.nih.gov/11228836/)
- Gehring, W. J., Liu, Y., Orr, J. M., & Carp, J. (2012). The error-related negativity (ERN/Ne). In S. J. Luck & E. Kappenman (Eds.), *Oxford handbook of event-related potential components* (pp. 231–291). Oxford University Press.
- Gehring, W. J. & Willoughby, A. R. (2002). The medial frontal cortex and the rapid processing of monetary gains and losses. *Science*, *295*(5563), 2279–2282. [https://doi.org/10.1126/scie](https://doi.org/10.1126/science.1066893295/5563/2279) [nce.1066893295/5563/2279](https://doi.org/10.1126/science.1066893295/5563/2279)
- Gemba, H., Sasaki, K., & Brooks, V. B. (1986). "Error" potentials in limbic cortex (anterior cingulate area 24) of monkeys during motor learning. *Neuroscience Letters*, *70*(2), 223–227. [https://doi.org/0304-3940\(86\)90467-2](https://doi.org/0304-3940(86)90467-2)
- Gevins, A. & Smith, M. E. (2000). Neurophysiological measures of working memory and individual differences in cognitive ability and cognitive style. *Cerebral Cortex*, *10*(9), 829–839. https://pubmed.ncbi.nlm.nih.gov/10982744/
- Gevins, A., Smith, M. E., McEvoy, L. K., Leong, H., & Le, J. (1999). Electroencephalographic imaging of higher brain function. *Philosophical Transactions of the Royal Society of London Series B: Biological Sciences*, *354*(1387), 1125–1133.
- Gevins, A., Smith, M. E., McEvoy, L., & Yu, D. (1997). High-resolution EEG mapping of cortical activation related to working memory: Effects of task difficulty, type of processing, and practice. *Cerebral Cortex*, *7*(4), 374–385. https://pubmed.ncbi.nlm.nih.gov/9177767/
- Gilmore, C. S., Malone, S. M., & Iacono, W. G. (2010). Brain electrophysiological endophenotypes for externalizing psychopathology: A multivariate approach. *Behavior Genetics*, *40*(2), 186–200.
- Giraud, A.-L. L., Kleinschmidt, A., Poeppel, D., Lund, T. E., Frackowiak, R. S. J. J., & Laufs, H. (2007). Endogenous cortical rhythms determine cerebral specialization for speech perception and production. *Neuron*, *56*(6), 1127–1134. [https://doi.org/10.1016/j.neu](https://doi.org/10.1016/j.neuron.2007.09.038) [ron.2007.09.038](https://doi.org/10.1016/j.neuron.2007.09.038)
- Giraud, A.-L. L., & Poeppel, D. (2012). Cortical oscillations and speech processing: emerging computational principles and operations. *Nature Neuroscience*, *15*(4), 511–517. [https://doi.](https://doi.org/10.1038/nn.3063) [org/10.1038/nn.3063](https://doi.org/10.1038/nn.3063)
- Godlove, D. C., Emeric, E. E., Segovis, C. M., Young, M. S., Schall, J. D., & Woodman, G. F. (2011). Event-related potentials elicited by errors during the stop-signal task. I. Macaque monkeys. *The Journal of Neuroscience*, *31*(44), 15640–15649. [https://doi.org/10.1523/JNEURO](https://doi.org/10.1523/JNEUROSCI.3349-11.2011) [SCI.3349-11.2011](https://doi.org/10.1523/JNEUROSCI.3349-11.2011)
- Gorka, S. M., Burkhouse, K. L., Klumpp, H., Kennedy, A. E., Afshar, K., Francis, J., . . . Phan, K. L. (2018). Error-related brain activity as a treatment moderator and index of symptom change during cognitive-behavioral therapy or selective serotonin reuptake inhibitors. *Neuropsychopharmacology*, *43*(6), 1355–1363.
- Gratton, G. (2018). Brain reflections: A circuit-based framework for understanding information processing and cognitive control. *Psychophysiology*, *55*(3), 1–26. [https://doi.org/10.1111/](https://doi.org/10.1111/psyp.13038) [psyp.13038](https://doi.org/10.1111/psyp.13038)
- Gruber, W. R., Klimesch, W., Sauseng, P., & Doppelmayr, M. (2005). Alpha phase synchronization predicts P1 and N1 latency and amplitude size. *Cerebral Cortex*, *15*(4), 371–377. [https://](https://doi.org/10.1093/cercor/bhh139) [doi.org/10.1093/cercor/bhh139](https://doi.org/10.1093/cercor/bhh139)
FRONTAL MIDLINE THETA AS A MODEL SPECIMEN OF CORTICAL THETA 193
- Gruendler, T. O. J., Ullsperger, M., & Huster, R. J. (2011). Event-related potential correlates of performance-monitoring in a lateralized time-estimation task. *PloS One*, *6*(10), e25591.
- Hajcak, G., Moser, J. S., Yeung, N., & Simons, R. F. (2005). On the ERN and the significance of errors. *Psychophysiology*, *42*(2), 151–160.
- Hanslmayr, S., Pastotter, B., Bauml, K. H., Gruber, S., Wimber, M., & Klimesch, W. (2008). The electrophysiological dynamics of interference during the Stroop task. *Journal of Cognitive Neuroscience*, *20*(2), 215–225.
- Hanslmayr, S., Staudigl, T., Aslan, A., & Bauml, K. H. (2010). Theta oscillations predict the detrimental effects of memory retrieval. *Cognitive, Affective, and Behavioral Neuroscience*, *10*(3), 329–338. [doi: 10.3758/cabn.10.3.329](http://doi:%2010.3758/cabn.10.3.329%22)
- Hauser, T. U., Iannaccone, R., Stämpfli, P., Drechsler, R., Brandeis, D., Walitza, S., & Brem, S. (2014). The feedback-related negativity (FRN) revisited: New insights into the localization, meaning and network organization. *NeuroImage*, *84*, 159–168. [https://doi.org/10.1016/j.neu](https://doi.org/10.1016/j.neuroimage.2013.08.028) [roimage.2013.08.028](https://doi.org/10.1016/j.neuroimage.2013.08.028)
- Helfrich, R. F., Fiebelkorn, I. C., Szczepanski, S. M., Lin, J. J., Parvizi, J., Knight, R. T., & Kastner, S. (2018). Neural mechanisms of sustained attention are rhythmic. *Neuron*, *99*(4), 854–865. e5.
- Holroyd, C. B. (2002). A note on the oddball N200 and the feedback ERN. In M. Ullsperger & M. Falkenstein (Eds.), *Errors, conflicts and the brain. Current opinions on performance monitoring* (pp. 211–218). Max Planck Institute for Human Cognitive and Brain Sciences.
- Holroyd, C. B. & Coles, M. G. (2002). The neural basis of human error processing: reinforcement learning, dopamine, and the error-related negativity. *Psychological Review*, *109*(4), 679–709. https://pubmed.ncbi.nlm.nih.gov/12374324/
- Holroyd, C. B., Coles, M. G. H., Nieuwenhuis, S., Gehring, W. J., & Willoughby, A. R. (2002). Medial prefrontal cortex and error potentials. *Science*, *296*(5573), 1610–1611.
- Hsieh, L.-T., Ekstrom, A. D., & Ranganath, C. (2011). Neural oscillations associated with item and temporal order maintenance in working memory. *The Journal of Neuroscience*, *31*(30), 10803–10810.
- Hsieh, L. T. & Ranganath, C. (2014). Frontal midline theta oscillations during working memory maintenance and episodic encoding and retrieval. *NeuroImage*, *85*, 721–729. [https://doi.org/](https://doi.org/10.1016/j.neuroimage.2013.08.003) [10.1016/j.neuroimage.2013.08.003](https://doi.org/10.1016/j.neuroimage.2013.08.003)
- Huang, Y., Chen, L., & Luo, H. (2015). Behavioral oscillation in priming: Competing perceptual predictions conveyed in alternating theta-band rhythms. *Journal of Neuroscience*, *35*(6), 2830–2837.
- Huster, R. J., Eichele, T., Enriquez-Geppert, S., Wollbrink, A, Kugel, H., Konrad, C., & Pantev, C. (2011). Multimodal imaging of functional networks and event-related potentials in performance monitoring. *NeuroImage*, *56*(3), 1588–1597.
- Hyman, J. M., Hasselmo, M. E., & Seamans, J. K. (2011). What is the functional relevance of prefrontal cortex entrainment to hippocampal theta rhythms? *Frontiers in Neuroscience*, *5*, 1–13.
- Inouye, T., Shinosaki, K., Iyama, A., Matsumoto, Y., & Toi, S. (1994). Moving potential field of frontal midline theta activity during a mental task. *Cognitive Brain Research*, *2*, 87–92.
- Inouye, T., Shinosaki, K., Iyama, A., Matsumoto, Y., Toi, S., & Ishihar, T. (1994). Potential flow of frontal midline theta activity during a mental task in the human electroencephalogram. *Neuroscience Letters*, *169*, 145–148.
194 JAMES F. CAVANAGH and MICHAEL X COHEN
- Insel, T., Cuthbert, B., Garvey, M., Heinssen, R., Pine, D. S., Quinn, K., . . . Wang, P. (2010). Research domain criteria (RDoC): Toward a new classification framework for research on mental disorders. *American Journal of Psychiatry*, *167*(7), 748–751. [pii]10.1176/appi.ajp.2010.09091379
- Ishii, R., Shinosaki, K., Ukai, S., Inouye, T., Ishihara, T., Yoshimine, T., . . . Takeda, M. (1999). Medial prefrontal cortex generates frontal midline theta rhythm. *Neuroreport*, *10*(4), 675– 679. https://pubmed.ncbi.nlm.nih.gov/10208529/
- Itthipuripat, S., Wessel, J. R., & Aron, A. R. (2013). Frontal theta is a signature of successful working memory manipulation. *Experimental Brain Research*, *224*(2), 255–262. [https://doi.](https://doi.org/10.1007/s00221-012-3305-3) [org/10.1007/s00221-012-3305-3](https://doi.org/10.1007/s00221-012-3305-3)
- Jacobs, J., Hwang, G., Curran, T., & Kahana, M. J. (2006). EEG oscillations and recognition memory: Theta correlates of memory retrieval and decision making. *NeuroImage*, *32*(2), 978–987.
- Javitt, D. C., Lee, M., Kantrowitz, J. T., & Martinez, A. (2018). Mismatch negativity as a biomarker of theta band oscillatory dysfunction in schizophrenia. *Schizophrenia Research*, *191*, 51–60.
- Jensen, O. & Tesche, C. D. (2002). Frontal theta activity in humans increases with memory load in a working memory task. *European Journal of Neuroscience*, *15*(8), 1395–1399. [https://pub](https://pubmed.ncbi.nlm.nih.gov/11994134/) [med.ncbi.nlm.nih.gov/11994134/](https://pubmed.ncbi.nlm.nih.gov/11994134/)
- Jensen, O. & Colgin, L. L. (2007). Cross-frequency coupling between neuronal oscillations. *Trends in Cognitive Sciences*, *11*(7), 267–269.
- Jensen, O. & Lisman, J. E. (2005). Hippocampal sequence-encoding driven by a cortical multiitem working memory buffer. *Trends in Neurosciences*, *28*(2), 67–72. [https://doi.org/10.1016/](https://doi.org/10.1016/j.tins.2004.12.001) [j.tins.2004.12.001](https://doi.org/10.1016/j.tins.2004.12.001)
- Jocham, G. & Ullsperger, M. (2009). Neuropharmacology of performance monitoring. *Neuroscience and Biobehavioral Reviews*, *33*(1), 48–60.
- Jones, M. W. & Wilson, M. A. (2005a). Phase precession of medial prefrontal cortical activity relative to the hippocampal theta rhythm. *Hippocampus*, *15*(7), 867–873. [https://doi.org/](https://doi.org/10.1002/hipo.20119) [10.1002/hipo.20119](https://doi.org/10.1002/hipo.20119)
- Jones, M. W. & Wilson, M. A. (2005b). Theta rhythms coordinate hippocampal-prefrontal interactions in a spatial memory task. *PLoS Biology*, *3*(12), e402. [https://doi.org/10.1371/jour](https://doi.org/10.1371/journal.pbio.0030402) [nal.pbio.0030402](https://doi.org/10.1371/journal.pbio.0030402)
- Jutras, M. J., Fries, P., & Buffalo, E. A. (2013). Oscillatory activity in the monkey hippocampus during visual exploration and memory formation. *Proceedings of the National Academy of Sciences of the United States of America*, *110*(32), 13144–13149.
- Kahana, M. J., Sekuler, R., Caplan, J. B., Kirschen, M., & Madsen, J. R. (1999). Human theta oscillations exhibit task dependence during virtual maze navigation. *Nature*, *399*(6738), 781– 784.
- Kamarajan, C., Pandey, A. K., Chorlian, D. B., Manz, N., Stimus, A. T., Anokhin, A. P., . . . Porjesz, B. (2015). Deficient event-related theta oscillations in individuals at risk for alcoholism: A study of reward processing and impulsivity features. *PLoS One*, *10*(11), 1–32.
- Kang, S. J., Rangaswamy, M., Manz, N., Wang, J. C., Wetherill, L., Hinrichs, T., . . . Porjesz, B. (2012). Family-based genome-wide association study of frontal theta oscillations identifies potassium channel gene KCNJ6. *Genes, Brain and Behavior*, *11*(6), 712–719. [https://doi.org/](https://doi.org/10.1111/j.1601-183X.2012.00803.x) [10.1111/j.1601-183X.2012.00803.x](https://doi.org/10.1111/j.1601-183X.2012.00803.x)
FRONTAL MIDLINE THETA AS A MODEL SPECIMEN OF CORTICAL THETA 195
- Killian, N. J., Jutras, M. J., & Buffalo, E. A. (2012). A map of visual space in the primate entorhinal cortex. *Nature*, *491*(7426), 761–764.
- Klimesch, W. (1999). EEG alpha and theta oscillations reflect cognitive and memory performance: a review and analysis. *Brain Research: Brain Research Reviews*, *29*(2–3), 169–195. https://pubmed.ncbi.nlm.nih.gov/10209231/
- Klimesch, W., Doppelmayr, M., Schwaiger, J., Winkler, T., & Gruber, W. (2000). Theta oscillations and the ERP old/new effect: Independent phenomena? *Clinical Neurophysiology*, *111*(5), 781–793.
- Ko, D., Kwon, S., Lee, G. T., Im, C. H., Kim, K. H., & Jung, K. Y. (2012). Theta oscillation related to the auditory discrimination process in mismatch negativity: Oddball versus control paradigm. *Journal of Clinical Neurology (Korea)*, *8*(1), 35–42.
- Lee, H., Simpson, G. V., Logothetis, N. K., & Rainer, G. (2005). Phase locking of single neuron activity to theta oscillations during working memory in monkey extrastriate visual cortex. *Neuron*, *45*(1), 147–156.
- Lee, M., Balla, A., Sershen, H., Sehatpour, P., Lakatos, P., & Javitt, D. C. (2018). Rodent mismatch negativity/theta neuro-oscillatory response as a translational neurophysiological biomarker for N-methyl-D-aspartate receptor-based new treatment development in schizophrenia. *Neuropsychopharmacology*, *43*(3), 571–582. [https://doi.org/10.1038/](https://doi.org/10.1038/npp.2017.176) [npp.2017.176](https://doi.org/10.1038/npp.2017.176)
- Liebe, S., Hoerzer, G. M., Logothetis, N. K., & Rainer, G. (2012). Theta coupling between V4 and prefrontal cortex predicts visual short-term memory performance. *Nature Neuroscience*, *15*(3), 456–462, S1-2.
- Light, G. A., Swerdlow, N. R., Thomas, M. L., Calkins, M. E., Green, M. F., Greenwood, T. A., . . . Turetsky, B. I. (2015). Validation of mismatch negativity and P3a for use in multisite studies of schizophrenia: Characterization of demographic, clinical, cognitive, and functional correlates in COGS-2. *Schizophrenia Research*, *163*(1–3), 63–72. [https://doi.org/](https://doi.org/10.1016/j.schres.2014.09.042) [10.1016/j.schres.2014.09.042](https://doi.org/10.1016/j.schres.2014.09.042)
- Lubenov, E. V. & Siapas, A. G. (2009). Hippocampal theta oscillations are travelling waves. *Nature*, *459*(7246), 534–539.
- Luschei, E. S. (2006). Patterns of laryngeal electromyography and the activity of the respiratory system during spontaneous laughter. *Journal of Neurophysiology*, *96*(1), 442–450. [https://doi.](https://doi.org/10.1152/jn.00102.2006) [org/10.1152/jn.00102.2006](https://doi.org/10.1152/jn.00102.2006)
- Luu, P. & Tucker, D. M. (2001). Regulating action: Alternating activation of midline frontal and motor cortical networks. *Clinical Neurophysiology*, *112*(7), 1295–1306. [https://doi.org/S1388-](https://doi.org/S1388-2457(01)00559-4) [2457\(01\)00559-4](https://doi.org/S1388-2457(01)00559-4) [pii]
- Luu, P., Tucker, D. M., & Makeig, S. (2004). Frontal midline theta and the error-related negativity: Neurophysiological mechanisms of action regulation. *Clinical Neurophysiology*, *115*(8), 1821–1835. [pii]
- MacNeilage, P. F. & Davis, B. L. (2001). Motor mechanisms in speech ontogeny: Phylogenetic, neurobiological and linguistic implications. *Current Opinion in Neurobiology*, *11*(6), 696– 700. [https://doi.org/10.1016/S0959-4388\(01\)00271-9](https://doi.org/10.1016/S0959-4388(01)00271-9)
- Macrides, F., Eichenbaum, H., & Forbes, W. B. (1982). Temporal relationship between sniffing and the limbic theta rhythm during odor discrimination reversal learning. *Journal of Neuroscience*, *2*(12), 1705–1717.
- Miltner, W. H. R., Braun, C. H., & Coles, M. G. H. (1997). Event-related brain potentials following incorrect feedback in a time-estimation task: Evidence for a "generic" neural system for error detection. *Journal of Cognitive Neuroscience*, *9*(6), 788–798.
196 JAMES F. CAVANAGH and MICHAEL X COHEN
- Mitchell, D. J., McNaughton, N., Flanagan, D., & Kirk, I. J. (2008). Frontal-midline theta from the perspective of hippocampal "theta". *Progress in Neurobiology*, *86*(3), 156–185. [https://doi.](https://doi.org/10.1016/j.pneurobio.2008.09.005) [org/10.1016/j.pneurobio.2008.09.005](https://doi.org/10.1016/j.pneurobio.2008.09.005)
- Mizuki, Y., Kajimura, N., Kai, S., Suetsugi, M., Ushijima, I., & Yamada, M. (1992). Differential responses to mental stress in high and low anxious normal humans assessed by frontal midline theta activity. *International Journal of Psychophysiology*, *12*, 169–178.
- Mizuki, Y., Suetsugi, M., Ushijima, I., & Yamada, M. (1996). Differential effects of noradrenergic drugs on anxiety and arousal in healthy volunteers with high and low anxiety. *Progress in Neuro-Psychopharmacology & Biological Psychiatry*, *20*(8), 1353–1367.
- Mizuki, Y, Suetsugi, M., Ushijima, I., & Yamada, M. (1997). Differential effects of dopaminergic drugs on anxiety and arousal in healthy volunteers with high and low anxiety. *Progress in Neuro-Psychopharmacology & Biological Psychiatry*, *21*(4), 573–590. [http://www.ncbi.nlm.](http://www.ncbi.nlm.nih.gov/pubmed/9194141) [nih.gov/pubmed/9194141](http://www.ncbi.nlm.nih.gov/pubmed/9194141)
- Moran, T. P., Bernat, E. M., Aviyente, S., Schroder, H. S., & Moser, J. S. (2014). Sending mixed signals: Worry is associated with enhanced initial error processing but reduced call for subsequent cognitive control. *Social Cognitive and Affective Neuroscience*, *10*(11), 1548–1556.
- Moser, J. S., Moran, T. P., Schroder, H. S., Donnellan, M. B., & Yeung, N. (2013). On the relationship between anxiety and error monitoring: A meta-analysis and conceptual framework. *Frontiers in Human Neuroscience*, *7*, 466.
- Munneke, G.-J., Nap, T. S., Schippers, E. E., & Cohen, M. X. (2015). A statistical comparison of EEG time- and time–frequency domain representations of error processing. *Brain Research*, *1618*, 222–230.
- Narayanan, N. S., Cavanagh, J. F., Frank, M. J., & Laubach, M. (2013). Common medial frontal mechanisms of adaptive control in humans and rodents. *Nature Neuroscience*, *16*, 1–10.
- Nigbur, R., Cohen, M. X., Ridderinkhof, K. R., & Stürmer, B. (2012). Theta dynamics reveal domain-specific control over stimulus and response conflict. *Journal of Cognitive Neuroscience*, *24*(5), 1264–1274.
- Nyhus, E., & Curran, T. (2010). Functional role of gamma and theta oscillations in episodic memory. *Neuroscience and Biobehavioral Reviews*, *34*(7), 1023–1035. [https://doi.org/10.1016/](https://doi.org/10.1016/j.neubiorev.2009.12.014) [j.neubiorev.2009.12.014](https://doi.org/10.1016/j.neubiorev.2009.12.014)
- Oehrn, C. R., Hanslmayr, S., Fell, J., Deuker, L., Kremers, N. A., Do Lam, A. T., . . . Axmacher, N. (2014). Neural communication patterns underlying conflict detection, resolution, and adaptation. *Journal of Neuroscience*, *34*(31), 10438–10452. [https://doi.org/10.1523/JNEURO](https://doi.org/10.1523/JNEUROSCI.3099-13.2014) [SCI.3099-13.2014](https://doi.org/10.1523/JNEUROSCI.3099-13.2014)
- Onton, J., Delorme, A., & Makeig, S. (2005). Frontal midline EEG dynamics during working memory. *NeuroImage*, *27*(2), 341–356.
- Pailing, P. E. & Segalowitz, S. J. (2004). The effects of uncertainty in error monitoring on associated ERPs. *Brain and Cognition*, *56*(2), 215–233.
- Parker, K. L., Chen, K.-H., Kingyon, J. R., Cavanagh, J. F., & Narayanan, N. S. (2015). Medial frontal ~4-Hz activity in humans and rodents is attenuated in PD patients and in rodents with cortical dopamine depletion. *Journal of Neurophysiology*, *114*(2), 1310–1320. [https://doi.](https://doi.org/10.1152/jn.00412.2015) [org/10.1152/jn.00412.2015](https://doi.org/10.1152/jn.00412.2015)
- Pastötter, B., Hanslmayr, S., & Bauml, K.-H. T. (2010). Conflict processing in the anterior cingulate cortex constrains response priming. *NeuroImage*, *50*(4), 1599–1605. [https://doi.org/](https://doi.org/10.1016/j.neuroimage.2010.01.095) [10.1016/j.neuroimage.2010.01.095](https://doi.org/10.1016/j.neuroimage.2010.01.095)
FRONTAL MIDLINE THETA AS A MODEL SPECIMEN OF CORTICAL THETA 197
- Paz, R., Bauer, E. P., & Pare, D. (2008). Theta synchronizes the activity of medial prefrontal neurons during learning. *Learning & Memory*, *15*(7), 524–531. [https://doi.org/10.1101/](https://doi.org/10.1101/lm.932408) [lm.932408](https://doi.org/10.1101/lm.932408)
- Pellegrino, F., Coupé, C., & Marsico, E. (2011). Across-language perspective on speech information rate. *Language*, *87*(3), 539–558.
- Petajan, J. H. & Williams, D. D. (1972). Behavior of single motor units during pre-shivering tone and shivering tremor. *American Journal of Physical Medicine*, *51*(1), 16–22.
- Phillips, J. M. & Everling, S. (2014). Event-related potentials associated with performance monitoring in non-human primates. *NeuroImage*, *97*, 308–320. [https://doi.org/10.1016/j.neu](https://doi.org/10.1016/j.neuroimage.2014.04.028) [roimage.2014.04.028](https://doi.org/10.1016/j.neuroimage.2014.04.028)
- Phillips, J. M., Vinck, M., Everling, S., & Womelsdorf, T. (2013). A long-range fronto-parietal 5- to 10-Hz network predicts "top-down" controlled guidance in a task-switch paradigm. Cerebral Cortex, *24*(8), 1996–2008.
- Pignatelli, M., Beyeler, A., & Leinekugel, X. (2012). Neural circuits underlying the generation of theta oscillations. *Journal of Physiology*, *106*(3–4), 81–92. [https://doi.org/10.1016/j.jphyspa](https://doi.org/10.1016/j.jphysparis.2011.09.007) [ris.2011.09.007](https://doi.org/10.1016/j.jphysparis.2011.09.007)
- Popov, T., Westner, B. U., Silton, R. L., Sass, S. M., Spielberg, J. M., Rockstroh, B., . . . Miller, G. A. (2018). Time course of brain network reconfiguration supporting inhibitory control. *The Journal of Neuroscience*, *38*(18), 2639–17.
- Raghavachari, S., Lisman, J. E., Tully, M., Madsen, J. R., Bromfield, E. B., & Kahana, M. J. (2006). Theta oscillations in human cortex during a working-memory task: Evidence for local generators. *Journal of Neurophysiology*, *95*(3), 1630–1638. [doi: 10.1152/](http://doi:%2010.1152/jn.00409.2005%22) [jn.00409.2005](http://doi:%2010.1152/jn.00409.2005%22)
- Rajan, A., Siegel, S. N., Liu, Y., Bengson, J., Mangun, G. R., & Ding, M. (2018). Theta oscillations index frontal decision-making and mediate reciprocal frontal–parietal interactions in willed attention. *Cerebral Cortex*, *29*(7), 2832–2843 .
- Rangaswamy, M., Jones, K. A., Porjesz, B., Chorlian, D. B., Padmanabhapillai, A., Kamarajan, C., . . . Begleiter, H. (2007). Delta and theta oscillations as risk markers in adolescent offspring of alcoholics. *International Journal of Psychophysiology*, *63*(1), 3–15. [https://doi.org/](https://doi.org/10.1016/j.ijpsycho.2006.10.003) [10.1016/j.ijpsycho.2006.10.003](https://doi.org/10.1016/j.ijpsycho.2006.10.003)
- Reinhart, R. M. G. & Woodman, G. F. (2014). Causal control of medial-frontal cortex governs electrophysiological and behavioral indices of performance monitoring and learning. *Journal of Neuroscience*, *34*(12), 4214–4227.
- Reinhart, R. M. G. (2017). Disruption and rescue of interareal theta phase coupling and adaptive behavior. *Proceedings of the National Academy of Sciences of the United States of America*, *114*(43), 11542–11547.
- Reinhart, R. M. G., Zhu, J., Park, S., & Woodman, G. F. (2015). Synchronizing theta oscillations with direct-current stimulation strengthens adaptive control in the human brain. *Proceedings of the National Academy of Sciences of the United States of America*, *112*(30), 9448–9453.
- Riesel, A., Goldhahn, S., & Kathmann, N. (2017). Hyperactive performance monitoring as a transdiagnostic marker: Results from health anxiety in comparison to obsessive– compulsive disorder. *Neuropsychologia*, *96*, 1–8. [https://doi.org/10.1016/j.neuropsycholo](https://doi.org/10.1016/j.neuropsychologia.2016.12.029) [gia.2016.12.029](https://doi.org/10.1016/j.neuropsychologia.2016.12.029)
- Rizzuto, D. S., Madsen, J. R., Bromfield, E. B., Schulze-Bonhage, A., & Kahana, M. J. (2006). Human neocortical oscillations exhibit theta phase differences between encoding and retrieval. *NeuroImage*, *31*(3), 1352–1358. [doi: 10.1016/j.neuroimage.2006.01.009](http://doi:%2010.1016/j.neuroimage.2006.01.009%22)
198 JAMES F. CAVANAGH and MICHAEL X COHEN
- Rizzuto, D. S., Madsen, J. R., Bromfield, E. B., Schulze-Bonhage, A., Seelig, D., Aschenbrenner-Scheibe, R., & Kahana, M. J. (2003). Reset of human neocortical oscillations during a working memory task. *Proceedings of the National Academy of Sciences of the United States of America*, *100*(13), 7931–7936. [https://doi.org/10.1073/pnas.07320611000732061100 \[pii\]](https://doi.org/10.1073/pnas.07320611000732061100%20[pii])
- Roberts, B. M., Hsieh, L. T., & Ranganath, C. (2013). Oscillatory activity during maintenance of spatial and temporal information in working memory. *Neuropsychologia*, *51*(2), 349–357.
- Rothé, M., Quilodran, R., Sallet, J., & Procyk, E. (2011). Coordination of high gamma activity in anterior cingulate and lateral prefrontal cortical areas during adaptation. *The Journal of Neuroscience*, *31*(31), 11110–11117.
- Ryman, S. G., Cavanagh, J. F., Wertz, C. J., Shaff, N. A., Dodd, A. B., Stevens, B., . . . Mayer, A. R. (2018). Impaired midline theta power and connectivity during proactive cognitive control in schizophrenia. *Biological Psychiatry*, *84*(9), 675–683. [https://doi.org/10.1016/j.biops](https://doi.org/10.1016/j.biopsych.2018.04.021) [ych.2018.04.021](https://doi.org/10.1016/j.biopsych.2018.04.021)
- Sato, K. (1952). On the theta rhythms in healthy human EEG. *Folia Psychiatrica et Neurologica*, *5*(4), 283–297.
- Sauseng, P., Griesmayr, B., Freunberger, R., & Klimesch, W. (2010). Control mechanisms in working memory: A possible function of EEG theta oscillations. *Neuroscience and Biobehavioral Reviews*, *34*(7), 1015–1022. doi: 10.1016/j.neubiorev.2009.12.006
- Sauseng, P., Klimesch, W., Doppelmayr, M., Hanslmayr, S., Schabus, M., & Gruber, W. R. (2004). Theta coupling in the human electroencephalogram during a working memory task. *Neuroscience Letters*, *354*(2), 123–126. [doi: 10.1016/j.neulet.2003.10.002](http://doi:%2010.1016/j.neulet.2003.10.002%22)
- Schmidt, B., Kanis, H., Holroyd, C. B., Miltner, W. H. R., & Hewig, J. (2018). Anxious gambling: Anxiety is associated with higher frontal midline theta predicting less risky decisions. *Psychophysiology*, *55*(10), 1–9.
- Shackman, A. J., Salomons, T. V, Slagter, H. A, Fox, A. S., Winter, J. J., & Davidson, R. J. (2011). The integration of negative affect, pain and cognitive control in the cingulate cortex. *Nature Reviews. Neuroscience*, *12*(3), 154–167.
- Siapas, A. G., Lubenov, E. V, & Wilson, M. A. (2005). Prefrontal phase locking to hippocampal theta oscillations. *Neuron*, *46*(1), 141–151.
- Smit, A. S., Eling, P. A T. M., & Coenen, A. M. L. (2004). Mental effort affects vigilance enduringly: after-effects in EEG and behavior. *International Journal of Psychophysiology*, *53*(3), 239–243.
- Smit, A. S., Eling, P. A T. M., Hopman, M. T., & Coenen, A. M. L. (2005). Mental and physical effort affect vigilance differently. *International Journal of Psychophysiology*, *57*(3), 211–217.
- Smith, E. H., Banks, G. P., Mikell, C. B., Cash, S. S., Patel, S. R., Eskandar, E. N., & Sheth, S. A. (2015). Frequency-dependent representation of reinforcement-related information in the human medial and lateral prefrontal cortex. *Journal of Neuroscience*, *35*(48), 15827–15836.
- Solomon, E. A., Kragel, J. E., Sperling, M. R., Sharan, A., Worrell, G., Kucewicz, M., . . . Kahana, M. J. (2017). Widespread theta synchrony and high-frequency desynchronization underlies enhanced cognition. *Nature Communications*, *8*, 1704. [https://doi.org/10.1038/s41](https://doi.org/10.1038/s41467-017-01763-2) [467-017-01763-2](https://doi.org/10.1038/s41467-017-01763-2)
- Staudigl, T., Hanslmayr, S., & Bauml, K. H. (2010). Theta oscillations reflect the dynamics of interference in episodic memory retrieval. *Journal of Neuroscience*, *30*(34), 11356–11362. doi:10.1523/JNEUROSCI.0637-10.2010
FRONTAL MIDLINE THETA AS A MODEL SPECIMEN OF CORTICAL THETA 199
- Swart, J. C., Frank, M. J., Määttä, J. I., Jensen, O., Cools, R., & den Ouden, H. E. M. (2018). Frontal network dynamics reflect neurocomputational mechanisms for reducing maladaptive biases in motivated action. *PLoS Biology* [online], 1–25. [https://doi.org/10.1371/journal.](https://doi.org/10.1371/journal.pbio.2005979) [pbio.2005979](https://doi.org/10.1371/journal.pbio.2005979)
- Talairach, J., Bancaud, J., Geier, S., Bordas-Ferrer, M., Bonis, A., Szikla, G., & Rusu, M. (1973). The cingulate gyrus and human behaviour. *Electroencephalography and Clinical Neurophysiology*, *34*(1), 45–52. doi: 10.1016/0013-4694(73)90149-1
- Tang, H., Yu, H. Y., Chou, C. C., Crone, N. E., Madsen, J. R., Anderson, W. S., & Kreiman, G. (2016). Cascade of neural processing orchestrates cognitive control in human frontal cortex. *ELife*, *5*, e12352.
- Taub, A. H., Perets, R., Kahana, E., & Paz, R. (2018). Oscillations synchronize amygdala-to-prefrontal primate circuits during aversive learning. *Neuron*, *97*(2), 291–298.e3. [https://doi.org/](https://doi.org/10.1016/j.neuron.2017.11.042) [10.1016/j.neuron.2017.11.042](https://doi.org/10.1016/j.neuron.2017.11.042)
- Töllner, T., Wang, Y., Makeig, S., Müller, H. J., Jung, T.-P., & Gramann, K. (2017). Two independent frontal midline theta oscillations during conflict detection and adaptation in a Simon-type manual reaching task. *The Journal of Neuroscience*, *37*(9), 2504–2515. [https://doi.](https://doi.org/10.1523/JNEUROSCI.1752-16.2017) [org/10.1523/JNEUROSCI.1752-16.2017](https://doi.org/10.1523/JNEUROSCI.1752-16.2017)
- Tóth, B., Kardos, Z., File, B., Boha, R., Stam, C. J., & Molnár, M. (2014). Frontal midline theta connectivity is related to efficiency of WM maintenance and is affected by aging. *Neurobiology of Learning and Memory*, *114*, 58–69.
- Trujillo, L. T. & Allen, J. J. (2007). Theta EEG dynamics of the error-related negativity. *Clinical Neurophysiology*, *118*(3), 645–668. [doi: 10.1016/j.clinph.2006.11.009](http://doi:%2010.1016/j.clinph.2006.11.009%22)
- Tsujimoto, S., Genovesio, A., & Wise, S. P. (2010). Evaluating self-generated decisions in frontal pole cortex of monkeys. *Nature Neuroscience*, *13*(1), 120–126.
- Tsujimoto, T., Shimazu, H., & Isomura, Y. (2006). Direct recording of theta oscillations in primate prefrontal and anterior cingulate cortices. *Journal of Neurophysiology*, *95*(5), 2987– 3000. doi:10.1152/jn.00730.2005
- van de Vijver, I., Cohen, M. X., & Ridderinkhof, K. R. (2014). Aging affects medial but not anterior frontal learning-related theta oscillations. *Neurobiology of Aging*, *35*(3), 692–704.
- van de Vijver, I., Ridderinkhof, K. R., & Cohen, M. X. (2011). Frontal oscillatory dynamics predict feedback learning and action adjustment. *Journal of Cognitive Neuroscience*, *23*(12), 4106–4121. [https://doi.org/10.1162/jocn\\_a\\_00110](https://doi.org/10.1162/jocn_a_00110)
- van Driel, J., Ridderinkhof, K. R., & Cohen, M. X. (2012). Not all errors are alike: Theta and alpha EEG dynamics relate to differences in error-processing dynamics. *The Journal of Neuroscience*, *32*(47), 16795–16806.
- van Noordt, S. J. R. & Segalowitz, S. J. (2012). Performance monitoring and the medial prefrontal cortex: A review of individual differences and context effects as a window on self-regulation. *Frontiers in Human Neuroscience*, *6*, 197. [https://doi.org/10.3389/](https://doi.org/10.3389/fnhum.2012.00197) [fnhum.2012.00197](https://doi.org/10.3389/fnhum.2012.00197)
- Van Veen, V. & Carter, C. S. (2002). The timing of action-monitoring processes in the anterior cingulate cortex. *Journal of Cognitive Neuroscience*, *14*(4), 593–602. [https://doi.org/10.1162/](https://doi.org/10.1162/08989290260045837) [08989290260045837](https://doi.org/10.1162/08989290260045837)
- VanRullen, R. (2016). Perceptual cycles. *Trends in Cognitive Sciences*, *20*(10), 723–735. [https://](https://doi.org/10.1016/j.tics.2016.07.006) [doi.org/10.1016/j.tics.2016.07.006](https://doi.org/10.1016/j.tics.2016.07.006)
- Verguts, T. (2017). Binding by random bursts: A computational model of cognitive control. *Journal of Cognitive Neuroscience*, *29*(6), 1103–1118. [https://doi.org/10.1162/jocn\\_a\\_01117](https://doi.org/10.1162/jocn_a_01117)
200 JAMES F. CAVANAGH and MICHAEL X COHEN
- Vezoli, J. & Procyk, E. (2009). Frontal feedback-related potentials in nonhuman primates: modulation during learning and under haloperidol. *Journal of Neuroscience*, *29*(50), 15675–15683. doi:10.1523/JNEUROSCI.4943-09.2009
- Vidal, F., Burle, B., Bonnet, M., Grapperon, J., & Hasbroucq, T. (2003). Error negativity on correct trials: a reexamination of available data. *Biological Psychology*, *64*(3), 265–282.
- Vidal, F., Hasbroucq, T., Grapperon, J., & Bonnet, M. (2000). Is the "error negativity" specific to errors? *Biological Psychology*, *51*(2–3), 109–128. [https://doi.org/10.1016/](https://doi.org/10.1016/S0301-0511(99)00032-0) [S0301-0511\(99\)00032-0](https://doi.org/10.1016/S0301-0511(99)00032-0)
- Vissers, M. E., Ridderinkhof, K. R., Cohen, M. X., & Slagter, H. A. (2018). Oscillatory mechanisms of response conflict elicited by color and motion direction: An individual differences approach. *Journal of Cognitive Neuroscience*, *30*(4), 468–481. [https://doi.org/](https://doi.org/10.1162/jocn_a_01222) [10.1162/jocn\\_a\\_01222](https://doi.org/10.1162/jocn_a_01222)
- Walsh, M. M. & Anderson, J. R. (2012). Learning from experience: Event-related potential correlates of reward processing, neural adaptation, and behavioral choice. *Neuroscience and Biobehavioral Reviews*, *36*(8), 1870–1884.
- Wang, C., Ulbert, I., Schomer, D. L., Marinkovic, K., & Halgren, E. (2005). Responses of human anterior cingulate cortex microdomains to error detection, conflict monitoring, stimulusresponse mapping, familiarity, and orienting. *Journal of Neuroscience*, *25*(3), 604–613. doi:10.1523/JNEUROSCI.4151-04.2005
- Wang, D., Clouter, A., Chen, Q., Shapiro, K. L., & Hanslmayr, S. (2018). Single-trial phase entrainment of theta oscillations in sensory regions predicts human associative memory performance. *The Journal of Neuroscience*, *38*(28), 0349–18.
- Wascher, E., Rasch, B., Sänger, J., Hoffmann, S., Schneider, D., Rinkenauer, G., . . . Gutberlet, I. (2014). Frontal theta activity reflects distinct aspects of mental fatigue. *Biological Psychology*, *96*, 57–65.
- Wessel, J. R. (2018). An adaptive orienting theory of error processing. *Psychophysiology*, *55*(3), 1–21.
- White, J. A., Banks, M. I., Pearce, R. A., & Kopell, N. J. (2000). Networks of interneurons with fast and slow gamma-aminobutyric acid type A (GABAA) kinetics provide substrate for mixed gamma–theta rhythm. *Proceedings of the National Academy of Sciences of the United States of America*, *97*(14), 8128–8133.
- Wiecki, T. V. & Frank, M. J. (2013). A computational model of inhibitory control in frontal cortex and basal ganglia. *Psychological Review*, *120*(2), 329–355.
- Womelsdorf, T., Johnston, K., Vinck, M., & Everling, S. (2010). Theta-activity in anterior cingulate cortex predicts task rules and their adjustments following errors. *Proceedings of the National Academy of Sciences of the United States of America*, *107*(11), 5248–5253. [doi: 10.1073/](http://doi:%2010.1073/pnas.0906194107%22) [pnas.0906194107](http://doi:%2010.1073/pnas.0906194107%22)
- Womelsdorf, T., Schoffelen, J. M., Oostenveld, R., Singer, W., Desimone, R., Engel, A. K., & Fries, P. (2007). Modulation of neuronal interactions through neuronal synchronization. *Science*, *316*(5831), 1609–1612. doi:10.1126/science.1139597
- Womelsdorf, T., Valiante, T. A., Sahin, N. T., Miller, K. J., & Tiesinga, P. (2014). Dynamic circuit motifs underlying rhythmic gain control, gating and integration. *Nature Neuroscience*, *17*(8), 1031–1039.
- Womelsdorf, T., Vinck, M., Leung, L. S., & Everling, S. (2010). Selective theta-synchronization of choice-relevant information subserves goal-directed behavior. *Frontiers in Human Neuroscience*, *4*, 210.
FRONTAL MIDLINE THETA AS A MODEL SPECIMEN OF CORTICAL THETA 201
- Yamaguchi, M., Crump, M. J. C., & Logan, G. D. (2013). Speed-accuracy trade-off in skilled typewriting: Decomposing the contributions of hierarchical control loops. *Journal of Experimental Psychology: Human Perception and Performance*, *39*(3), 678–699.
- Yordanova, J, Falkenstein, M., Hohnsbein, J., & Kolev, V. (2004). Parallel systems of error processing in the brain. *NeuroImage*, *22*(2), 590–602. [https://doi.org/10.1016/j.neuroim](https://doi.org/10.1016/j.neuroimage.2004.01.040S1053811904000850) [age.2004.01.040S1053811904000850](https://doi.org/10.1016/j.neuroimage.2004.01.040S1053811904000850) [pii]
- Yordanova, Juliana, Kolev, V., Rosso, O. A., Schürmann, M., Sakowitz, O. W., Özgören, M., & Basar, E. (2002). Wavelet entropy analysis of event-related potentials indicates modalityindependent theta dominance. *Journal of Neuroscience Methods*, *117*(1), 99–109. [https://doi.](https://doi.org/10.1016/S0165-0270(02)00095-X) [org/10.1016/S0165-0270\(02\)00095-X](https://doi.org/10.1016/S0165-0270(02)00095-X)
- Zavala, B. A., Tan, H., Little, S., Ashkan, K., Hariz, M., Foltynie, T., . . . Brown, P. (2014). Midline frontal cortex low-frequency activity drives subthalamic nucleus oscillations during conflict. *Journal of Neuroscience*, *34*(21), 7322–7333.
- Zavala, B., Brittain, J.-S., Jenkinson, N., Ashkan, K., Foltynie, T., Limousin, P., . . . Brown, P. (2013). Subthalamic nucleus local field potential activity during the Eriksen Flanker task reveals a novel role for theta phase during conflict monitoring. *The Journal of Neuroscience*, *33*(37), 14758–14766.
- Zavala, B., Tan, H., Little, S., Ashkan, K., Green, A. L., Aziz, T., . . . Brown, P. (2016). Decisions made with less evidence involve higher levels of corticosubthalamic nucleus theta band synchrony. *Journal of Cognitive Neuroscience*, *28*(6), 811–825. [https://doi.org/10.1162/jocn\\_](https://doi.org/10.1162/jocn_a_00934) [a\\_00934](https://doi.org/10.1162/jocn_a_00934)
- Zhang, H., Watrous, A. J., Patel, A., & Jacobs, J. (2018). Theta and alpha oscillations are traveling waves in the human neocortex. *Neuron*, *98*(6), 1269–1281.e4. [https://doi.org/10.1016/j.neu](https://doi.org/10.1016/j.neuron.2018.05.019) [ron.2018.05.019](https://doi.org/10.1016/j.neuron.2018.05.019)
- Zlojutro, M., Manz, N., Rangaswamy, M., Xuei, X., Flury-Wetherill, L., Koller, D., . . . Almasy, L. (2011). Genome-wide association study of theta band event-related oscillations identifies serotonin receptor gene HTR7 influencing risk of alcohol dependence. *American Journal of Medical Genetics, Part B: Neuropsychiatric Genetics*, *156*(1), 44–58. [https://doi.org/10.1002/](https://doi.org/10.1002/ajmg.b.31136) [ajmg.b.31136](https://doi.org/10.1002/ajmg.b.31136)
## [CHAPTER 10](#page-6-2)
# [THE ROLE OF ALPHA AND](#page-6-2) [BETA OSCILL ATIONS IN](#page-6-2) [THE HUMAN EEG DURING](#page-6-2) [PERCEPTION AND MEMORY](#page-6-2) [PROCESSES](#page-6-2)
SEBASTIAN MICHELMANN, BENJAMIN GRIFFITHS, AND SIMON HANSLMAYR
# **10.1 Alpha oscillations and their relation to cognition**
In 1929 a German physician named Hans Berger recorded the first human EEG. The first thing he noticed was a regular oscillation with a frequency of 10 Hz (Berger, 1929), which he termed alpha oscillations. Many decades after Berger discovered these alpha oscillations researchers use them as a first quality check of their EEG signal. After attaching electrodes to the subject's head, the researcher typically asks the subject to close their eyes and relax; the researcher then sees beautiful alpha waves with a frequency of around 10 Hz being maximal over posterior channels. When the subject then opened their eyes, alpha oscillations largely reduce. This phenomenon is extremely reliable, such that not seeing the reduction in alpha amplitude when subjects open their eyes would typically indicate that something went wrong. Reductions in alpha amplitude occur in all ranges of cognitive tasks such as visual processing (Adrian, 1944), auditory processing (Krause et al., 1994; Obleser & Weisz, 2012), somatosensory processing (Crone et al., 1998), memory encoding (Hanslmayr et al., 2009; Klimesch et al., 1996), memory retrieval (Burgess & Gruzelier, 2000; Waldhauser et al., 2016), working memory maintenance (Sauseng et al., 2009), decision making (Pornpattananangkul THE ROLE OF ALPHA AND BETA OSCILLATIONS IN THE HUMAN EEG 203
et al., 2019), and motor preparation and execution (Pfurtscheller et al., 1997). The exact frequency at which power reductions are maximal varies between tasks and often involves the faster beta oscillation around 15 Hz, which can be considered the "fast" sibling of alpha. In this chapter we therefore do not distinguish between alpha and beta oscillations and refer to these oscillations as alpha/beta. Suppression of alpha/beta oscillations is not only observed in humans, but also in a wide range of animals, for example, non-human primates (Haegens et al., 2011), dogs (Lopes da Silva et al., 1980), cats (von Stein et al., 2000), rodents (Wiest & Nicolelis, 2003), and even insects (Popov & Szyszka, 2019). This ubiquity of alpha/beta power suppression across cognitive domains and across the animal kingdom indicates that alpha/beta power reductions are a signature of an extremely general mechanism, which is called upon in almost any cognitive task and has been retained over millions of years of evolution. What could this mechanism be? This chapter attempts to answer this question.
Before delving into the different physiological interpretations of alpha oscillations it is worth pointing out a theoretical caveat that has become evident in cognitive neuroscience and the way we can avoid these problems. Historically the job description for a cognitive neuroscientist was to pick a cognitive phenomenon (i.e., attention, memory) and then find the "neural correlate" of that phenomenon. To demonstrate this approach let us consider a short thought experiment involving two hypothetical cognitive neuroscientists: AC and BD. Researcher AC is interested in attention. She runs several meticulously controlled experiments that all manipulate certain aspects of attention while she records EEG. Across this series of experiments, she finds that alpha oscillations are very consistently modulated by attention. She goes to a conference, presents her results, and concludes that alpha oscillations are *the* neural correlate of attention. At that same conference, researcher BD, who is interested in memory, also presents his results. In a series of carefully controlled experiments he shows that alpha oscillations are reliably modulated by various memory processes. He concludes his talk with saying that alpha oscillations are *the* neural correlate of memory.
So, who is right? What cognitive function do alpha oscillations represent: memory or attention? The answer is both are wrong. The error that both scientists make is to assume that there is a one-to-one mapping between neural phenomena and cognitive functions. This error has become known under the term "reverse inference error", that is, observing neural signature X has no predictive value for cognitive process Y to occur (Poldrack, 2011). With respect to alpha oscillations, given their ubiquity in terms of cognitive tasks (from attention to decision making) and species (from human to honeybees) it is evident that the task of trying to attach one particular label from cognitive psychology (attention vs. memory) to them is bound to fail. An alternative approach is needed if we want to truly understand the function of alpha oscillations. This alternative approach needs to avoid limiting itself by definitions of cognitive processes. Instead, this approach needs to embrace the fact that a given neural phenomenon can be of service to many different cognitive processes in many different species. One such alternative is to assume that different oscillations implement canonical computations (Siegel et al., 2012; Womelsdorf et al., 2014), which are basic neural operations that are called upon by 204 SEBASTIAN MICHELMANN et al.
different cognitive processes. Regulating the balance between excitation and inhibition, for instance, would be one such basic operation. Another basic operation is to enable the neural representation of information rich content. These operations arguably are required by almost any cognitive task and species. The difference from this approach to the traditional cognitive neuroscience approach is not in using different labels, but to try to understand the computational utility of a neural operation for a given cognitive process (see Buzsaki, 2019 for a similar line of argument). Instead of asking what the neural correlate of attention is, we ask how a decrease in alpha oscillations can be of service for attention, memory, decision making, etc. Section 10.2 provides a brief overview of the behaviour of alpha oscillations in terms of frequency, power, and phase. It is critical to understand these terms first before we can consider the physiological interpretations of alpha oscillations.
# **10.2 Signal properties of alpha: Frequency, Power, and Phase**
## **10.2.1 Frequency**
Analyzing alpha oscillations typically involves transforming an EEG signal into timefrequency space (see Cohen, 2014 for an excellent overview of the different methods and hands-on tutorials). Figure 10.1A shows a typical example of a raw EEG trace in a healthy human subject. It is easy to spot the decrease in alpha amplitudes at time 0 (when a stimulus was presented). Brain oscillations are defined by three physical properties: (i) frequency (Figure 10.1B), (ii) amplitude (Figure 10.1C), and (iii) phase (Figure 10.1D). Different brain networks are hypothesized to oscillate at different frequencies (Keitel & Gross, 2016), with small networks oscillating at fast frequencies (>40 Hz) and large networks oscillating at slower frequencies (<20 Hz) (von Stein & Sarnthein, 2000). Small and large here refers to the number of neurons involved in generating the signal. This anatomical property is reflected in the 1/F power ratio of EEG signals, which refers to the drop in signal power with increasing frequency. Alpha oscillations are remarkable because they stand out from the 1/F pattern (Figure 10.1B), which shows that they are a particularly strong oscillation recruiting large pools of neurons. Frequencies are typically used to distinguish between different types of oscillations, that is, theta ~ 4 Hz, beta ~15 Hz, gamma ~ 40 Hz, etc. The frequency within an oscillation has been shown to be linked to interindividual variability in memory processes (Cohen, 2011) or intelligence (Anokhin & Vogel, 1996). Recent work demonstrates that the frequency of alpha can also change within a subject, from trial-to-trial (Haegens et al., 2014) and may reflect cortical excitability ( Cohen, 2014). Therefore, it is important to consider that the frequency of alpha may vary from individual to individual and even from trial to trial within a participant. Sometimes it can even be challenging to distinguish a "fast theta" from a "slow alpha".
THE ROLE OF ALPHA AND BETA OSCILLATIONS IN THE HUMAN EEG 205

**Figure 10.1** Alpha oscillations and their parameters. (A) An example of a raw signal as recorded with a parietal EEG electrode is shown on the left. A stimulus was presented at time 0. The plot on the right shows the results of a time-frequency analysis in which power is depicted for each time-point (x-axis) and frequency band (y-axis; a.u. = arbitrary units). (B) A schematic of a typical EEG power spectrum is shown, with frequency on the x-axis and power on the y-axis. The inverse relationship between the size of neural assemblies and power is depicted. Note the peak at the alpha frequency which violates the 1/F relation between power and frequency. (C) A typical time-frequency plot showing event related power increases (hot colors) and decreases (cold colors) during processing of verbal information. Note the power increases in theta (3–7 Hz) and gamma (35–100 Hz) and the power decreases in alpha (8–12 Hz) and beta (13–35 Hz). (D) The relationship between EEG phase (top) and firing rates (bottom) is shown. The differently colored lines show phase modulations in trials with high (red), medium (purple) or low (blue) power.
(A) Reprinted with permission from Hanslmayr et al., 2011. (C) is modified and reprinted with permission from Hanslmayr et al., 2012. (D) modified and reprinted with permission from Jacobs et al., 2007.
#### **10.2.2 Power**
The power of an oscillation refers to its signal strength. It is usually calculated by taking the square of the signal. In human EEG, a signal is generated by the summation of several millions of postsynaptic potentials (inhibitory and excitatory) over an area of some cm2 (Pfurtscheller et al., 1996). Importantly, the current changes induced by postsynaptic potentials are tiny and we record these potentials with an electrode that is attached to the scalp, separated by various layers of bone, cerebrospinal fluid, skin, etc., from the brain. Therefore, in order to detect a signal that is large enough to be visible in the EEG, tens of thousands of post-synaptic potentials must come together in time. To give an analogy, recording EEG is a bit like recording the noise in a football stadium with one 206 SEBASTIAN MICHELMANN et al.
big microphone hanging from the ceiling. Using this coarse signal we cannot stand the chance to tune in onto an individual conversation between two fans, but we can use the signal to tell whether a goal was scored (because thousands of fans start shouting at the same time). Accordingly, the strength of an oscillation is assumed to reflect the degree of synchrony between inhibitory or excitatory postsynaptic potentials to an underlying neural assembly. Power increases indicate increased local synchrony whereas power decreases indicate de-synchronized local activity. This idea is reflected in the classic work of Pfurtscheller & Aranibar (1977), who coined the terms event-related synchronization and de-synchronization (ERS/ERD), which denotes power increases and decreases in response to an event or stimulus, respectively. In EEG experiments absolute power is usually transformed into power changes in response to a baseline (e.g., prestimulus interval). Figure 10.1C shows a typical example of such data with stimulus driven power increases in the lower (1–8 Hz: delta/theta) and higher (40–100 Hz; gamma) frequency ranges, and power decreases in the middle frequency ranges (8–35 Hz; alpha/beta).
#### **10.2.3 Phase**
The phase of an oscillation specifies the current position in a given cycle (Figure 10.1D), that is whether the oscillation exhibits a peak, trough, or zero crossing. Because the EEG reflects the sum of postsynaptic input to a given neuron, we can assume that it impinges on the neuron's probability to fire an action potential. Figure 10.1D shows a single neuron recorded in the human brain, and that the neuron is more likely to fire in the trough of the oscillation, which indeed resembles the time point of maximally coinciding excitatory input (note that the LFP in this case is measured in the extracellular space; therefore, negativity indexes excitation). This same figure also shows that the modulation of firing rate is stronger for trials of high power (red) and lower for trials of low power (blue). We can therefore assume that the phase of alpha oscillations (or any other oscillation for that matter) represent discrete time windows for neural firing, and that this synchronizing effect scales with power. This is a very useful computational property as it gives alpha oscillations the power to control the timing of neural firing in large groups of neurons. Like the conductor of an orchestra, who tells individual instruments when to play a particular note (and when to not play a note), alpha oscillations can synchronize large groups of neurons to temporally structure neural processing. This aspect becomes particularly important in Section 10.5, which covers the role of alpha phase for sampling information and replaying this information from memory.
# **10.3 Alpha Oscillations: Passive idling versus active inhibition**
Alpha oscillations decrease in amplitude when a subject is engaged in a task as opposed to when a subject is resting (especially with eyes closed). This goes against intuition THE ROLE OF ALPHA AND BETA OSCILLATIONS IN THE HUMAN EEG 207
as one would usually expect to see an increase in brain signal strength when a subject performs a challenging task, not a decrease. How can we functionally interpret this negative relationship between alpha power and cognitive processing? Up until the early 2000s the prevailing view was that alpha oscillations reflect a state of "idling" or rest. In their article, Pfurtscheller and colleagues (1996) give the example of the motor cortex, in particular the visual cortex and the hand area during a reading task or a motor task requiring finger movements, respectively. During reading, the visual cortex displays profound alpha-power decreases, whereas the hand motor area shows an increase in alpha power. This picture switches when the subject engages in a motor task requiring finger movement. Within the idling hypothesis, one would interpret the increased alpha power over areas that are not required by the task as "nil work", that is, a passive resonance phenomenon of a part of cortex that has "nothing to do" (Adrian & Matthews, 1934). Since almost any cognitive task always involves specific activation of some regions and de-activation of other regions (Fox et al., 2005) the EEG would always reflect some areas that show alpha power decreases (or desynchronization) and some areas that show alpha-power increases (or synchronization). The important emphasis of the idling hypothesis is on the passive aspect of alpha synchronization which has no functional role per se.
Klimesch and colleagues (2007) and Jensen and Mazaheri (2010) presented a contrasting view to the idling hypothesis and suggested that alpha oscillations play a critical role in cognitive processing. The seminal findings that led to this interpretation were studies showing that alpha power *increased* with increasing cognitive load in a working memory task (Jensen et al., 2002; Klimesch et al., 1999). This alpha- power increase with cognitive load is difficult to reconcile with the idling hypothesis, which led to the active inhibition hypothesis (Jensen & Mazaheri, 2010; Klimesch et al., 2007). Within the active inhibition hypothesis an increase in alpha power reflects an active inhibition process that serves to silence a particular region that is task irrelevant. This silencing of task-irrelevant areas ensures that information is processed selectively in task-relevant areas and protects the processing of this information from interference or noise. A critical prediction that the inhibition account made was that an increase in alpha oscillations narrows the time windows for neurons to fire (see red vs. blue lines in Figure 10.1D) and therefore reduces neural firing. Thus, periods of high alpha power should coincide with low neural firing, whereas periods of low alpha power should coincide with high neural firing. This prediction was confirmed in a non-human primate study (Haegens et al., 2011), which suggests that an increase in alpha power in a given area acts as a "silencing mechanism" which muffles neural assemblies that otherwise might interfere.
Coming back to our example, alpha synchronization of the hand area while reading this chapter ensures that you can focus on the text instead of moving around (or thinking about movements). The more challenging a task, the more we need to tune out task-irrelevant activity. The inhibition account has gained considerable support over the last decades because it can accommodate the findings in the literature better than the idling hypothesis. To give two examples, if subjects maintain visual content in working 208 SEBASTIAN MICHELMANN et al.
memory that was presented in the left hemifield, therefore being processed in the right occipital cortex, alpha power increases over the left occipital cortex (Sauseng et al., 2009). Externally enhancing alpha power with repetitive transcranial magnetic stimulation over the irrelevant hemisphere then increases working memory performance. Similar evidence comes from Bonnefond and Jensen (2012), who demonstrated that subjects actively increase their alpha power in anticipation of a task-irrelevant distractor presented during working memory maintenance. The more the subjects upregulated alpha power the better the performance on the working memory task. These results rule out a passive perspective of alpha oscillations and instead suggest that alpha oscillations are very much an active process that regulates neural activity to ensure selective information processing. Within this perspective, alpha oscillations serve the function of a filter that tunes out task-irrelevant information to render the task-relevant signal more salient.
# **10.4 Alpha Power Decreases and the Representation of Information**
The active inhibition account has been extremely useful in interpreting the role of alpha power increases, or alpha synchronization during cognitive processing. This is because any cognitive process requires selective information processing; alpha oscillations, by inhibiting task irrelevant neural assemblies, ensure such selective information processing. This functional interpretation of alpha oscillations is broad enough to accommodate the fact that modulations of alpha oscillations are observed in a variety of cognitive tasks and species. Returning to the thought experiment from earlier, the attention scientist AC and memory scientist BD would interpret their findings to show that both memory and attention crucially rely on an active filtering mechanism. Indeed, alpha power increases over areas that hold the representation of *task-irrelevant* information, regardless of whether this information is currently perceived (Thut et al., 2006; Worden et al., 2000), held in working memory (Sauseng et al., 2009), or stored in longterm memory (Waldhauser et al., 2012). The emphasis of the active inhibition hypothesis is on alpha synchronization and its computational utility in terms of providing a filter mechanism for selective information processing. What is less clear from this perspective, however, is what the computational utility of alpha power decreases are for information processing (other than allowing for increased neural spike rates through less inhibition). We therefore proposed an additional theory, which is complementary to the inhibition account. Within this framework we emphasized the role of alpha power decreases in allowing for high-fidelity information to be represented in neural assemblies. A key assumption of this account rests on the fact the alpha/beta power decreases represent periods of de-correlated neural firing (see Murthy & Fetz, 1996 for such a demonstration for beta oscillations in the motor cortex).
THE ROLE OF ALPHA AND BETA OSCILLATIONS IN THE HUMAN EEG 209
One way of interpreting the functional utility of de-correlated firing in alpha for cognitive processing applies tenets of information theory (Shannon & Weaver, 1949) to neural oscillations. This framework is known as the "information-via-desynchronization hypothesis" (Hanslmayr et al., 2012), which proposes that synchronized alpha/beta states are inherently bad for information representation as neuronal activity is highly redundant. Take the simplified instance of two presynaptic neurons that act upon the same postsynaptic neuron: if one presynaptic neuron fires in perfect synchrony with another, what can this neuron add to the neuronal code that its synchronous partner does not already (Schneidman et al., 2011)? If we expand this principle to networks of neurons, we can postulate that highly synchronous networks are detrimental to information processing, because they only represent redundancies. To overcome this limitation therefore, the networks must desynchronize. Through desynchronization, the underlying neural code can be more complex and hence convey a more detailed representation of information. The event-related desynchronization so commonly seen in alpha oscillation may be a prime example of this phenomenon.
Numerous studies support the idea that alpha/beta power decreases reflect the representation of information within the cortex. One of the most direct lines of support comes from a recent simultaneous EEG-fMRI experiment by Griffiths and colleagues (2019), who asked participants to associate video clips with words, and to later recall the clips using the words as a cue (Figure 10.2). For each trial, the researchers quantified the amount of visual information present in the cortex by conducting representational similarity analysis (RSA) on the fMRI data (Kriegeskorte et al., 2008). RSA is based on correlations of neural patterns and reasons that representations of the same content should elicit neural patterns that are more alike than the patterns elicited by representations of different content (Kriegeskorte et al., 2008). The researchers then asked whether the power of the alpha and beta frequencies (8–30Hz) correlated with the quantity of information (calculated via RSA) represented on a given trial. Indeed, they found evidence to suggest a parametric link between alpha/beta power and information: as power decreased, information increased (Figure 10.2b). Similarly, Hanslmayr and colleagues (2009) presented participants with words and asked them to engage in semantic processing (i.e., does this word represent a living entity or a non-living entity?) or shallow processing (i.e., does the first letter of the word precede the last in the alphabet?). As semantic processing involves much greater levels of information processing (you must not only process the letters, but also what those letters mean), the researchers hypothesized that alpha/beta power decreases would be greater during this type of processing. Their results revealed just that—suggesting that alpha/beta power decreases scale with the depth of information processing (see Fellner et al., 2018 for similar results contrasting familiar and unfamiliar stimuli). In conjunction with a number of other studies, these results strongly implicate alpha/beta power reductions in information processing (Hanslmayr et al., 2012).
While the alpha idling theory assumes that synchronous alpha oscillations mark a default state in which the cortex does nothing (Pfurtscheller et al., 1996), the alpha inhibition theory highlights the active role of alpha synchronization in the suppression of
210 SEBASTIAN MICHELMANN et al.

**Figure 10.2** Alpha power and information processing. (A) Infographic depicting theories behind alpha and information processing. Perception and memory retrieval involve the processing of large quantities of information. The noise correlation account proposes that when task irrelevant neurons (in blue) synchronize (e.g., during the interval), they mask the signal generated by task-relevant neurons (in red). When the task-irrelevant neurons desynchronize however (i.e., during perception/retrieval), the signal can be detected above the background noise. The information-via-desynchronization account proposes that oscillatory desynchronization allows a more complex neural code to be generated. Such a complex code is necessary to process the highly complex information encountered in daily life. In both instances, oscillatory desynchronization benefits information processing (B) Reproduction of the results by Griffiths and colleagues. Power decreases during both perception and retrieval negatively correlate with the amount of stimulus specific information present on that trial.
task irrelevant information (Jensen & Mazaheri, 2010; Klimesch et al., 2007). It therefore attributes an operative function to alpha synchrony. The information via desynchronization hypothesis goes beyond the inhibition theory, in that it highlights the active role of power decreases for the processing of information. Therein, power decreases are not a mere absence of inhibition, but rather functionally involved in neural computations. The crucial insight is that in order to process complex information or represent information rich content, synchronous neural activity does not provide enough coding space. Desynchronous neural activity on the other hand, which is marked by power decreases in the alpha/beta band, provides the required coding space through locally decoupled neural assemblies. The information via desynchronization theory therefore stresses that, in order to perform cognitive operations that work on complex and informationrich content, alpha/beta power must decrease.
Another way to interpret the inverse relation between alpha power and information representation is offered by studies investigating "noise-correlations", which refers to correlated firing of task-irrelevant neurons—a process that can be detrimental to information representation (Mitchell et al., 2009). If two task-irrelevant neurons fire together, their noise is amplified. Expand this principle to hundreds or thousands of neurons and their noise becomes deafening. In such quantities, these noise correlations THE ROLE OF ALPHA AND BETA OSCILLATIONS IN THE HUMAN EEG 211
mask the signal generated by neurons critical to the task at hand (Averbeck et al., 2006; see also Figure 10.2a), leading to an impaired ability in processing and representing information. To rectify this situation, the magnitude of noise correlations needs to be attenuated. How, though, do noise correlations relate to alpha oscillations? Given that the summed electric potential of the correlated neurons creates a spike in the amplitude of local field potential (Averbeck et al., 2006), repeated and rhythmic patterns of noise correlations would create repeated and rhythmic increases in the amplitude of local field potential (LFP). As alpha oscillations dominate the neocortex, one may speculate that the rhythmic noise correlations may resonate within this frequency band. Under this assumption, periods of high-amplitude alpha oscillations would reflect periods of numerous noise correlations where information processing is inhibited. This interpretation conforms with the active inhibition account because it would allow alpha power increases to suppress task-irrelevant information. Periods of alpha desynchrony, in contrast, would reflect periods of limited noise correlations, where there is a greatest potential for information representation.
In summary, there are two theoretical arguments that implicate alpha power decreases in the representation of stimulus-specific information. The informationvia-desynchronization account suggests that alpha power reductions facilitate the evolution of more complex neural codes, which then allows for the representation of high-fidelity information in the cortex. The noise correlation account suggests that alpha power decreases reduce the background noise in the cortex, allowing for key signals to be more clearly communicated. Currently, empirical evidence supports both ideas by demonstrating that alpha power decreases scale with the quantity of information present in the cortex.
# **10.5 Alpha Phase: Information Sampling and Replay**
Recent evidence suggests that the continuous input that our brain receives from the outside world is not sampled continuously, but in discrete rhythmic steps around the alpha frequency (VanRullen, 2016). These studies show that the probability of detecting a briefly presented visual stimulus fluctuates rhythmically (VanRullen et al., 2007). This attentional sampling process has been suggested to operate at a frequency of roughly 8 Hz (Landau & Fries, 2012), even when sustained attention to the same object is maintained (Fiebelkorn & Kastner, 2019; Fiebelkorn et al., 2013). Overall, there appears to be a close correlation between the phase of an oscillation in the lower alpha band (around 8 Hz) and the perception of an incoming stimulus. In the perception of continuous and dynamic stimuli, the stimulus identity can be reliably decoded from the ongoing phase of neural oscillations. Therein, an individual continuous stimulus is associated with a unique time course of neural activity. Specifically, the stimulus 212 SEBASTIAN MICHELMANN et al.
entrains the cortical rhythm in a content-specific way that organizes neural firing (Ng et al., 2013). Interestingly, the phase of the ongoing oscillation contains more information about stimulus identity than its power (Schyns et al., 2011).
Considering this information sampling role of alpha phase in perception, an imminent question is whether or not the reinstatement of information from memory relies on the replay of that information sampled in the alpha frequency. To this end, alpha phase could index similar mechanisms during attention and memory, just like alpha power decreases. But how can we measure the information sampling and the replay thereof in the phase of a recorded EEG?
Similar to assessing the similarity of neural patterns in space, as is usually done in fMRI, one can assess the similarity of neural patterns in phase (over time) via the use of RSA methods (discussed earlier). Established measures of connectivity can help quantify the similarity of neural patterns in the phase of the alpha-frequency band (Greenblatt et al., 2012). Connectivity measures usually assess the similarity between different channels in their time course of activity. This typically measures shared information between regions. Yet, measures of connectivity will lend themselves perfectly to quantify representational similarity between encoding and retrieval (Figure 10.3a).
In a first study, we applied such similarity measures of phase in a human EEG experiment where subjects were instructed to encode and replay dynamic visual (short movie clips) or auditory stimuli (short melodies played by different instruments). Indeed, content-specific patterns of oscillatory phase in the lower alpha band during perception represent the identity of the visual or auditory stimuli in the visual and auditory cortex, respectively. Strikingly, these phase patterns reappear when representations of short video clips and short sound clips are replayed from memory (Michelmann et al., 2016). Importantly, this replay takes place in the absence of the dynamic stimulus itself and can be localized in sensory specific areas (Figure 10.3c). A recent study replicated this effect in the visual domain and demonstrated that the reinstatement of temporal patterns is only observed when content is successfully recalled, that is, temporal pattern reinstatement is implicated in successful memory (Michelmann et al., 2019). Another study replicated this effect during sleep, indicating that replay of stimulus-specific phase patterns supports memory consolidation (Schreiner et al., 2018). Further evidence documents that such content-specific phase patterns are also replayed when an association with a previously shown dynamic stimulus is formed (Michelmann et al., 2018).
Interestingly, the reinstatement of temporal patterns is not always beneficial for memory but can in some cases interfere with memory as demonstrated by studies which manipulated the contextual overlap between encoding and retrieval. For instance, (Staudigl et al., 2015) manipulated the context in which a word is learned and remembered by playing the same video clip in the background behind the word at encoding and at retrieval (context match); or playing a different video clip in the background behind the word at encoding and at retrieval (context mismatch). The importance of reinstatement of contextual information was observed via temporal and spatial pattern similarity in the beta frequency band. Specifically, higher pattern similarity was associated with better memory performance when contexts where matching. On the
THE ROLE OF ALPHA AND BETA OSCILLATIONS IN THE HUMAN EEG 213
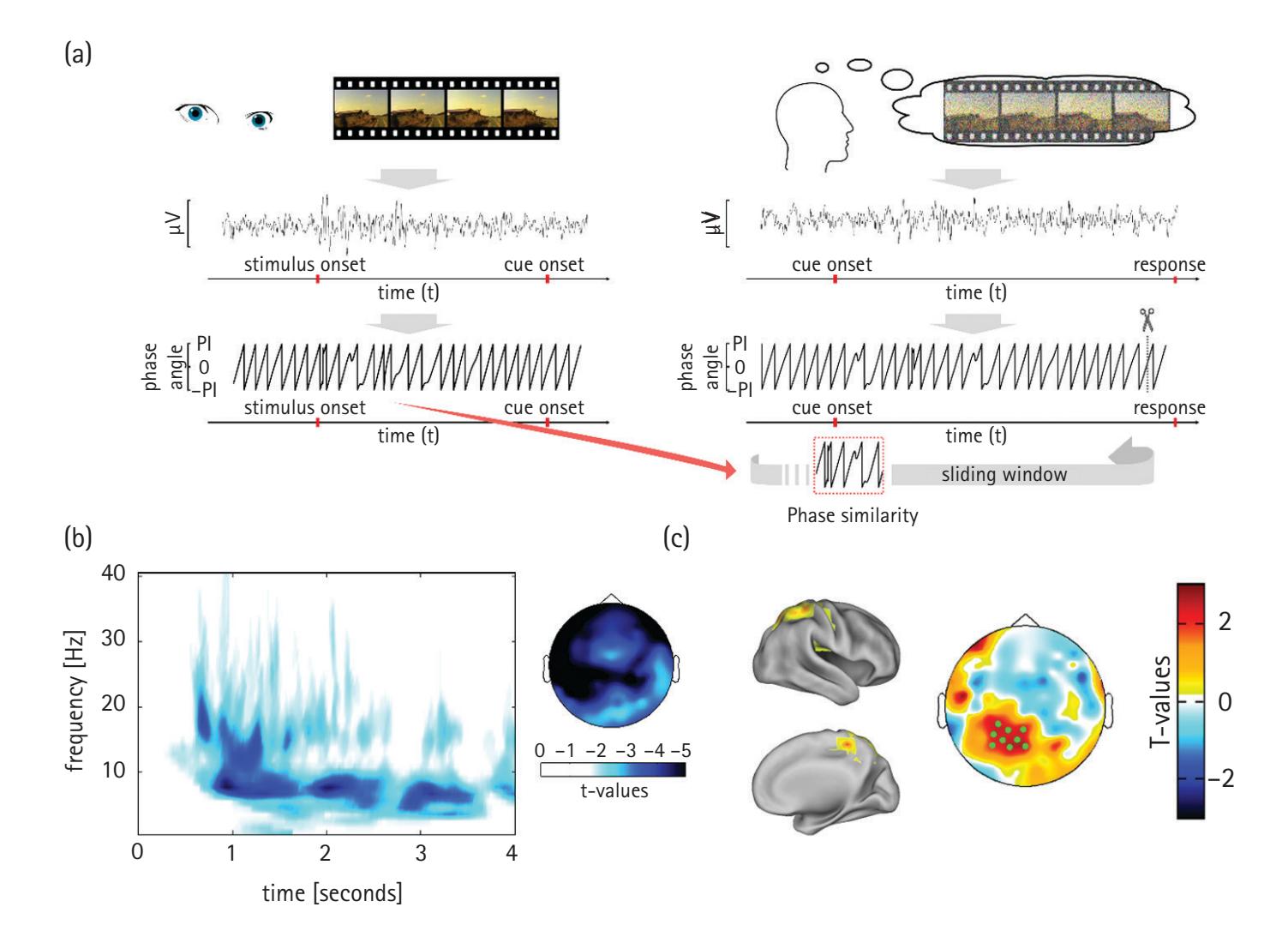
**Figure 10.3** Alpha power decreases during memory retrieval code stimulus-specific information. (A) Subjects first encoded a video (left). They later retrieved a vivid representation of that video from memory (right). The phase time course was extracted from the EEG during encoding and retrieval in order to calculate a similarity measure between encoding and retrieval. (B) During retrieval, strong and sustained alpha power decreases were observed. (C) Reactivation of stimulus-specific information, as measured with phase similarity, could be detected in the alpha frequency band with a maximum in parietal regions. This reactivation was localized in parietal cortex (C, left).
Reproduced from Michelmann et al., 2016.
other hand, non-overlapping contexts were characterized by more dissimilar patterns for remembered vs. forgotten words. These findings were recently replicated in a study using sensory modality (i.e., presenting a word visually or aurally) as a context match/ mismatch manipulation (Staudigl & Hanslmayr, 2019). The results of these studies are in line with the notion that context reinstatement is only helpful when the context has not changed and substantiate the importance of temporal patterns for content representation.
Most of the studies referenced earlier found that stimulus-specific information was coded in the phase of the lower alpha band, around 8 Hz (Michelmann et al., 2016, 2018; Michelmann et al., 2019; Staudigl & Hanslmayr, 2019). Corroborating evidence for a special role of 8 Hz in the sampling of memories comes from Kerren and colleagues (2018), who showed decoded content-specific representations in memory from spatial patterns of activity, and that these patterns fluctuate at a frequency of 8 Hz. The sampling of information at an 8 Hz rhythm therefore seems to underlie both, rhythmic sampling 214 SEBASTIAN MICHELMANN et al.
of information during perception (VanRullen et al., 2007) and the replay of that information during memory reinstatement.
## **10.6 Linking alpha phase and power**
Michelmann and colleagues (2016) showed that the frequency band that contains content-specific temporal patterns is also the one that displays the most prominent power decreases during retrieval (Figure 10.3b), and furthermore, they observed an interaction such that sensory areas that were involved in the reinstatement of auditory and visual temporal patterns also expressed stronger power decreases in the respective condition. This suggests that power decreases and the representation of information in oscillatory phase are not two separate processes but rather are intertwined. This raises the question as to how the two signal properties of alpha—power and phase—interact in the service of information representation.
We suggest that a decrease of power in an ongoing oscillation renders a signal less stationary (and therefore also less predictable) and thereby allows for a flexible adjustment of phase (Hanslmayr et al., 2016). These phase adjustments, or deviations from stationarity, make it possible that time courses in phase can represent stimulus specific patterns, and to replay these patterns from memory (Figure 10.4C). From an information theoretic view, a stationary oscillation without phase adjustments wouldn't

**Figure 10.4** Information coding properties for stationary and non-stationary signals is illustrated. (A) A stationary (high power) signal (orange) is shown together with its phase (blue) in the upper row. The lower row shows a less stationary signal. (B) Phases for each signal are shown every 100 ms (indicated by ticks in A). (C) Non-stationary signals allow for stimulus specific coding by assigning a different time course to each stimulus.
THE ROLE OF ALPHA AND BETA OSCILLATIONS IN THE HUMAN EEG 215
be able to represent much information in its phase because the time course of a stationary signal is perfectly predictable once the phase at one time point is known. For example, the signal in the top row of Figure 10.4A visits the same phase every 100 ms (top row in Figure 10.4B). Since information theory quantifies information as the inverse of the predictability (i.e., negative logarithm in the case of Shannon's Entropy, see Shannon & Weaver, 1949) we can infer that this signal has little potential to carry information. Indeed, if we were to code the identity of a stimulus in such a perfectly predictable signal, we would not be able to distinguish between different stimuli. In contrast, a non-stationary signal (lower row of Figure 10.4A), which has phase modulations, can carry much more information. In this case, the phase cannot be predicted from previous time points (lower panel in Figure 10.4B). This allows us to code different stimuli by assigning a phase time course to each stimulus (Figure 10.4C). This simple relationship between the power of a signal and predictability of phase time courses elegantly unifies the findings described in this chapter. To this end, a signal with high alpha power leads to a more stationary time course and thus inhibits information coding. In contrast, a signal with lower alpha power allows for a less stationary time course and therefore the coding of information. Importantly, this idea is in line with the general notion of an inhibitory role of alpha power increases but goes beyond the previous work in ascribing specific computational roles to power and phase in the service of representing information.
## **10.7 Concluding Remarks**
This chapter showed that alpha oscillations are ubiquitous as they are modulated by almost any task and can be observed in almost any animal. It therefore follows that alpha oscillations must perform a basic neural operation, which is of service for many cognitive operations. After an overview of the idling vs. inhibition hypothesis we then discussed the computational utility of alpha power reductions for information representation. We reviewed studies that demonstrated that alpha power reductions are intimately linked to information coding—specifically, these studies showed that stimulus-specific information is coded in the phase of alpha. Importantly, several studies demonstrated that this phase information is replayed when a reminder to that stimulus is presented. Finally, we illustrated how power decreases allow for less stationary phase time courses and consequently for information representation. Together, we conclude that alpha power decreases do play an important role for information representation—a neural operation needed in almost any task and in almost any animal.
An important crucial future question refers to the nature of the relationship between alpha power decreases and its role for coding information. If indeed, as we here suggest, alpha power decreases are mechanisms for representing information we should be able to manipulate perception, maintenance, and retrieval of information by directly manipulating alpha oscillations via brain stimulation techniques (Hanslmayr et al., 216 SEBASTIAN MICHELMANN et al.
2019). Such a demonstration of a causal relationship between alpha power decreases and the representation of information is crucial in order to show that alpha oscillations are indeed a mechanism for information representation, instead of a mere epiphenomenon.
#### **References**
- Adrian, E. D. (1944). Brain rhythms. *Nature*, *153*, 360–362.
- Adrian, E. D. & Matthews, B. H. (1934). The interpretation of potential waves in the cortex. *Journal of Physiology*, *81*(4), 440–471.
- Anokhin, A. & Vogel, F. (1996). EEG alpha rhythm frequency and intelligence in normal adults. *Intelligence*, *23*(1), 1–14. doi:10.1016/S0160-2896(96)80002-X
- Averbeck, B. B., Latham, P. E., & Pouget, A. (2006). Neural correlations, population coding and computation. *Nature Reviews Neuroscience*, *7*(5), 358–366. doi:10.1038/nrn1888
- Berger, H. (1929). Über das Elektrenkephalogramm des Menschen. *Archiv für Psychiatrie und Nervenkrankheiten*, *87*, 527–570.
- Bonnefond, M. & Jensen, O. (2012). Alpha oscillations serve to protect working memory maintenance against anticipated distracters. *Current Biology*, *22*(20), 1969–1974. doi:10.1016/ j.cub.2012.08.029
- Burgess, A. P. & Gruzelier, J. H. (2000). Short duration power changes in the EEG during recognition memory for words and faces. *Psychophysiology*, *37*(5), 596–606.
- Buzsaki, G. (2019). *The Brain from inside out*. Oxford University Press.
- Cohen, M. X. (2011). Hippocampal-prefrontal connectivity predicts midfrontal oscillations and long-term memory performance. *Current Biology*, *21*(22), 1900–1905. doi:10.1016/ j.cub.2011.09.036
- Cohen, M. X. (2014). *Analyzing neural time series data: Theory and practice*. MIT Press.
- Cohen, M. X. (2014). Fluctuations in oscillation frequency control spike timing and coordinate neural networks. *Journal of Neuroscience*, *34*(27), 8988–8998. doi:10.1523/ JNEUROSCI.0261-14.2014
- Crone, N. E., Miglioretti, D. L., Gordon, B., Sieracki, J. M., Wilson, M. T., Uematsu, S., & Lesser, R. P. (1998). Functional mapping of human sensorimotor cortex with electrocorticographic spectral analysis. I. Alpha and beta event-related desynchronization. *Brain*, *121(Pt 12*), 2271–2299.
- Fellner, M. C., Gollwitzer, S., Rampp, S., Kreiselmeyr, G., Bush, D., Diehl, B., . . . Hanslmayr, S. (2018). Spectral fingerprints or spectral tilt? Evidence for distinct oscillatory signatures of memory formation. https://journals.plos.org/plosbiology/article?id=10.1371/journal. pbio.3000403
- Fiebelkorn, I. C. & Kastner, S. (2019). A rhythmic theory of attention. *Trends in Cognitive Sciences*, *23*(2), 87–101. doi:10.1016/j.tics.2018.11.009
- Fiebelkorn, I. C., Saalmann, Y. B., & Kastner, S. (2013). Rhythmic sampling within and between objects despite sustained attention at a cued location. *Current Biology*, *23*(24), 2553–2558. doi:10.1016/j.cub.2013.10.063
- Fox, M. D., Snyder, A. Z., Vincent, J. L., Corbetta, M., Van Essen, D. C., & Raichle, M. E. (2005). The human brain is intrinsically organized into dynamic, anticorrelated functional networks. *Proceedings of the National Academy of Sciences of the United States of America*, *102*(27), 9673–9678. [doi:10.1073/pnas.0504136102](http://doi:10.1073/pnas.0504136102%22)
- Greenblatt, R. E., Pflieger, M. E., & Ossadtchi, A. E. (2012). Connectivity measures applied to human brain electrophysiological data. *Journal of Neuroscience Methods*, *207*(1), 1–16. doi:10.1016/j.jneumeth.2012.02.025
THE ROLE OF ALPHA AND BETA OSCILLATIONS IN THE HUMAN EEG 217
- Griffiths, B. J., Mayhew, S. D., Mullinger, K. J., Jorge, J., Charest, I., Wimber, M., & Hanslmayr, S. (2019). Alpha/beta power decreases track the fidelity of stimulus-specific information. https://elifesciences.org/articles/49562
- Haegens, S., Cousijn, H., Wallis, G., Harrison, P. J., & Nobre, A. C. (2014). Inter- and intraindividual variability in alpha peak frequency. *NeuroImage*, *92*, 46–55. doi:10.1016/ j.neuroimage.2014.01.049
- Haegens, S., Nacher, V., Luna, R., Romo, R., & Jensen, O. (2011). alpha-Oscillations in the monkey sensorimotor network influence discrimination performance by rhythmical inhibition of neuronal spiking. *Proceedings of the National Academy of Sciences of the United States of America*, *108*(48), 19377–19382. doi:10.1073/pnas.1117190108
- Hanslmayr, S., Axmacher, N., & Inman, C. S. (2019). Modulating human memory via entrainment of brain oscillations. *Trends in Neuroscience*, *42*(7), 485–499.
- Hanslmayr, S., Gross, J., Klimesch, W., & Shapiro, K. L. (2011). The role of α oscillations in temporal attention. *Brain Research Reviews*, *67*(1–2), 331–343.
- Hanslmayr, S., Spitzer, B., & Bauml, K. H. (2009). Brain oscillations dissociate between semantic and nonsemantic encoding of episodic memories. *Cerebral Cortex*, *19*(7), 1631–1640. doi:10.1093/cercor/bhn197
- Hanslmayr, S., Staresina, B. P., & Bowman, H. (2016). Oscillations and episodic memory: Addressing the synchronization/desynchronization conundrum. *Trends in Neuroscience*, *39*(1), 16–25. doi:10.1016/j.tins.2015.11.004
- Hanslmayr, S., Staudigl, T., & Fellner, M. C. (2012). Oscillatory power decreases and longterm memory: The information via desynchronization hypothesis. *Frontiers in Human Neuroscience*, *6*, 74. doi:10.3389/fnhum.2012.00074
- Jacobs, J., Kahana, M. J., Ekstrom, A. D., & Fried, I. (2007). Brain oscillations control timing of single-neuron activity in humans. *Journal of Neuroscience*, *27*(14), 3839–3844.
- Jensen, O., Gelfand, J., Kounios, J., & Lisman, J. E. (2002). Oscillations in the alpha band (9- 12 Hz) increase with memory load during retention in a short-term memory task. *Cerebral Cortex*, *12*(8), 877–882.
- Jensen, O. & Mazaheri, A. (2010). Shaping functional architecture by oscillatory alpha activity: gating by inhibition. *Frontiers in Human Neuroscience*, *4*, 186. doi:10.3389/ fnhum.2010.00186
- Keitel, A. & Gross, J. (2016). Individual human brain areas can be identified from their characteristic spectral activation fingerprints. *PLoS Biology*, *14*(6), e1002498. doi:10.1371/journal. pbio.1002498
- Kerren, C., Linde-Domingo, J., Hanslmayr, S., & Wimber, M. (2018). An optimal oscillatory phase for pattern reactivation during memory retrieval. *Current Biology*, *28*(21), 3383–3392 e3386. doi:10.1016/j.cub.2018.08.065
- Klimesch, W., Doppelmayr, M., Schwaiger, J., Auinger, P., & Winkler, T. (1999). 'Paradoxical' alpha synchronization in a memory task. *Brain Research: Cognitive Brain Research*, *7*(4), 493–501.
- Klimesch, W., Sauseng, P., & Hanslmayr, S. (2007). EEG alpha oscillations: the inhibition-timing hypothesis. *Brain Research Reviews*, *53*(1), 63–88. doi:10.1016/j.brainresrev.2006.06.003
- Klimesch, W., Schimke, H., Doppelmayr, M., Ripper, B., Schwaiger, J., & Pfurtscheller, G. (1996). Event-related desynchronization (ERD) and the Dm effect: Does alpha desynchronization during encoding predict later recall performance? *International Journal of Psychophysiology*, *24*(1-2), 47–60.
- Krause, C. M., Lang, H. A., Laine, M., Helle, S. I., Kuusisto, M. J., & Porn, B. (1994). Eventrelated desynchronization evoked by auditory stimuli. *Brain Topography*, *7*(2), 107–112.
218 SEBASTIAN MICHELMANN et al.
- Kriegeskorte, N., Mur, M., & Bandettini, P. (2008). Representational similarity analysis connecting the branches of systems neuroscience. *Frontiers in Systems Neuroscience*, *2*, 4. doi:10.3389/neuro.06.004.2008
- Landau, A. N. & Fries, P. (2012). Attention samples stimuli rhythmically. *Current Biology*, *22*(11), 1000–1004. doi:10.1016/j.cub.2012.03.054
- Lopes da Silva, F. H., Vos, J. E., Mooibroek, J., & Van Rotterdam, A. (1980). Relative contributions of intracortical and thalamo-cortical processes in the generation of alpha rhythms, revealed by partial coherence analysis. *Electroencephalography and Clinical Neurophysiology*, *50*(5-6), 449–456.
- Michelmann, S., Bowman, H., & Hanslmayr, S. (2016). The temporal signature of memories: Identification of a general mechanism for dynamic memory replay in humans. *PLoS Biology*, *14*(8), e1002528. doi:10.1371/journal.pbio.1002528
- Michelmann, S., Bowman, H., & Hanslmayr, S. (2018). Replay of stimulus-specific temporal patterns during associative memory formation. *Journal of Cognitive Neuroscience*, *30*(11), 1577–1589. doi:10.1162/jocn\_a\_01304
- Michelmann, S., Staresina, B. P., Bowman, H., & Hanslmayr, S. (2019). Speed of timecompressed forward replay flexibly changes in human episodic memory. *Nature Human Behaviour*, *3*(2), 143–154. doi:10.1038/s41562-018-0491-4
- Mitchell, J. F., Sundberg, K. A., & Reynolds, J. H. (2009). Spatial attention decorrelates intrinsic activity fluctuations in macaque area V4. *Neuron*, *63*(6), 879–888. doi:10.1016/j.neuron.2009.09.013
- Murthy, V. N. & Fetz, E. E. (1996). Synchronization of neurons during local field potential oscillations in sensorimotor cortex of awake monkeys. *Journal of Neurophysiology*, *76*(6), 3968–3982. doi:10.1152/jn.1996.76.6.3968
- Ng, B. S., Logothetis, N. K., & Kayser, C. (2013). EEG phase patterns reflect the selectivity of neural firing. *Cerebral Cortex*, *23*(2), 389–398. doi:10.1093/cercor/bhs031
- Obleser, J. & Weisz, N. (2012). Suppressed alpha oscillations predict intelligibility of speech and its acoustic details. *Cerebral Cortex*, *22*(11), 2466–2477. doi:10.1093/cercor/bhr325
- Pfurtscheller, G. & Aranibar, A. (1977). Event-related cortical desynchronization detected by power measurements of scalp EEG. *Electroencephalography and Clinical Neurophysiology*, *42*(6), 817–826.
- Pfurtscheller, G., Neuper, C., Andrew, C., & Edlinger, G. (1997). Foot and hand area mu rhythms. *International Journal of Psychophysiology*, *26*(1–3), 121–135.
- Pfurtscheller, G., Stancak, A., Jr., & Neuper, C. (1996). Event-related synchronization (ERS) in the alpha band--an electrophysiological correlate of cortical idling: a review. *International Journal of Psychophysiology*, *24*(1-2), 39–46.
- Poldrack, R. A. (2011). Inferring mental states from neuroimaging data: from reverse inference to large-scale decoding. *Neuron*, *72*(5), 692–697. doi:10.1016/j.neuron.2011.11.001
- Popov, T., & Szyszka, P. (2019). Alpha oscillations govern interhemispheric spike timing coordination in the honeybee brain. https://royalsocietypublishing.org/doi/10.1098/ rspb.2020.0115#:~:text=What%20is%20the%20function%20of,information%20 flow%20during%20spontaneous%20activity.
- Pornpattananangkul, N., Grogans, S., Yu, R., & Nusslock, R. (2019). Single-trial EEG dissociates motivation and conflict processes during decision-making under risk. *NeuroImage*, *188*, 483–501. doi:10.1016/j.neuroimage.2018.12.029
- Sauseng, P., Klimesch, W., Heise, K. F., Gruber, W. R., Holz, E., Karim, A. A., . . . Hummel, F. C. (2009). Brain oscillatory substrates of visual short-term memory capacity. *Current Biology*, *19*(21), 1846–1852. doi:10.1016/j.cub.2009.08.062
THE ROLE OF ALPHA AND BETA OSCILLATIONS IN THE HUMAN EEG 219
- Schneidman, E., Puchalla, J. L., Segev, R., Harris, R. A., Bialek, W., & Berry, M. J., 2nd. (2011). Synergy from silence in a combinatorial neural code. *Journal of Neuroscience*, *31*(44), 15732– 15741. doi:10.1523/JNEUROSCI.0301-09.2011
- Schreiner, T., Doeller, C. F., Jensen, O., Rasch, B., & Staudigl, T. (2018). Theta phase-coordinated memory reactivation reoccurs in a slow-oscillatory rhythm during NREM sleep. *Cell Reports*, *25*(2), 296–301. doi:10.1016/j.celrep.2018.09.037
- Schyns, P. G., Thut, G., & Gross, J. (2011). Cracking the code of oscillatory activity. *PLoS Biology*, *9*(5), e1001064. doi:10.1371/journal.pbio.1001064
- Shannon, C. E. & Weaver, W. (1949). *A mathematical theory of communication*. University of Illinois Press.
- Siegel, M., Donner, T. H., & Engel, A. K. (2012). Spectral fingerprints of large-scale neuronal interactions. *Nature Reviews Neuroscience*, *13*(2), 121–134. doi:10.1038/nrn3137
- Staudigl, T. & Hanslmayr, S. (2019). Reactivation of neural patterns during memory reinstatement supports encoding specificity. *Cognitive Neuroscience*, *10*(4), 175–185.
- Staudigl, T., Vollmar, C., Noachtar, S., & Hanslmayr, S. (2015). Temporal-pattern similarity analysis reveals the beneficial and detrimental effects of context reinstatement on human memory. *Journal of Neuroscience*, *35*(13), 5373–5384. doi:10.1523/JNEUROSCI.4198-14.2015
- Thut, G., Nietzel, A., Brandt, S. A., & Pascual-Leone, A. (2006). Alpha-band electroencephalographic activity over occipital cortex indexes visuospatial attention bias and predicts visual target detection. *Journal of Neuroscience*, *26*(37), 9494–9502. doi:10.1523/ JNEUROSCI.0875-06.2006
- VanRullen, R. (2016). Perceptual cycles. *Trends in Cognitive Sciences*, *20*(10), 723–735. doi:10.1016/j.tics.2016.07.006
- VanRullen, R., Carlson, T., & Cavanagh, P. (2007). The blinking spotlight of attention. *Proceedings of the National Academy of Sciences of the United States of America*, *104*(49), 19204–19209. doi:10.1073/pnas.0707316104
- von Stein, A., Chiang, C., & Konig, P. (2000). Top-down processing mediated by interareal synchronization. *Proceedings of the National Academy of Sciences of the United States of America*, *97*(26), 14748–14753. doi:10.1073/pnas.97.26.14748
- von Stein, A. & Sarnthein, J. (2000). Different frequencies for different scales of cortical integration: from local gamma to long range alpha/theta synchronization. *International Journal of Psychophysiology*, *38*(3), 301–313.
- Waldhauser, G. T., Braun, V., & Hanslmayr, S. (2016). Episodic memory retrieval functionally relies on very rapid reactivation of sensory information. *Journal of Neuroscience*, *36*(1), 251– 260. doi:10.1523/JNEUROSCI.2101-15.2016
- Waldhauser, G. T., Johansson, M., & Hanslmayr, S. (2012). alpha/beta oscillations indicate inhibition of interfering visual memories. *Journal of Neuroscience*, *32*(6), 1953–1961. doi:10.1523/JNEUROSCI.4201-11.2012
- Wiest, M. C. & Nicolelis, M. A. (2003). Behavioral detection of tactile stimuli during 7-12 Hz cortical oscillations in awake rats. *Nature Neuroscience*, *6*(9), 913–914. doi:10.1038/nn1107
- Womelsdorf, T., Valiante, T. A., Sahin, N. T., Miller, K. J., & Tiesinga, P. (2014). Dynamic circuit motifs underlying rhythmic gain control, gating and integration. *Nature Neuroscience*, *17*(8), 1031–1039. doi:10.1038/nn.3764
- Worden, M. S., Foxe, J. J., Wang, N., & Simpson, G. V. (2000). Anticipatory biasing of visuospatial attention indexed by retinotopically specific alpha-band electroencephalography increases over occipital cortex. *Journal of Neuroscience*, *20*(6), RC63.
## [CHAPTER 11](#page-6-3)
# [Theory and Research](#page-6-3) [on Asymmetric Frontal](#page-6-3) [Cortical Activit y](#page-6-3) [as Assessed by EEG](#page-6-3) [Frequency Analyses](#page-6-3)
EDDIE HARMON-JONES, TAYLOR POPP, AND PHILIP A. GABLE
Frequency analyses of electroencephalographic (EEG) activity have played a major role in research and theory concerning the role of left versus right frontal cortical activity in emotion- and motivation-related phenomena. In this work, researchers have focused primarily on alpha power (8–13 Hz) activity in the left versus right frontal regions. This focus on alpha power was based on other research suggesting that alpha power is inversely related to cortical activity (Cook et al., 1998; Davidson et al., 1990).
Much of this research has used the difference between the left and right frontal region as the variable of interest. The use of difference scores is based on past research using a variety of methods that suggest with regard to emotion- and motivation-related variables, one frontal hemispheric region may be inhibiting the opposite frontal hemispheric region (Schutter, 2009; Schutter et al., 2001). The corpus callosum, the largest white matter bundle connecting the left and right hemispheres, likely plays a critical role in this asymmetric functioning of the frontal cortices (Schutter & Harmon-Jones, 2013). Given this, researchers typically subtract left frontal alpha power from right frontal alpha power (after the values are log transformed to normalize the distributions, e.g., log F4 minus log F3). The resulting metric is then referred to as *relative left or relative right frontal activity*, depending on whether the difference score is a more positive (relative left) or a more negative (relative right) numeric value.
ASYMMETRIC FRONTAL CORTICAL ACTIVITY 221
# **11.1 Definitions of Psychological Concepts: Affective Valence and Motivational Direction**
We begin by providing our definitions of the psychological concepts of affective valence and motivational direction. Affective valence denotes whether an affective trait or state is positive or negative. Although affective valence can be defined in a number of ways (Harmon-Jones & Gable, 2018; Lazarus, 1991), we define it as the subjective feel of the affect (emotion or mood; affect encompasses both of these latter concepts). Affective experiences that organisms like feeling are positive, and affective experiences that organisms dislike feeling are negative (Harmon-Jones et al., 2011).
Motivational direction refers to the urge to move toward (approach) or away (withdrawal) from something (Harmon-Jones et al., 2013; Gable & Dreisbach, 2021). Many theories suggest that approach motivation is triggered by rewards, desired outcomes, or positive goals, and that withdrawal (avoidance) motivation is triggered by punishments, undesired outcomes, or negative goals. The anticipations of these end-products may inspire much approach and withdrawal motivation, but these anticipations are not the only causes of approach and withdrawal motivation and they should therefore not be part of the definition. That is, approach and withdrawal motivation can occur without being prompted by these anticipations (for an extended discussion, see Harmon-Jones et al., 2013).
# **11.2 Affective Valence and Asymmetric Frontal Cortical Activity**
Beginning in the 1930s, research using a variety of methods suggested that the left and right frontal cortices are involved in different emotional (affective) responses. For example, lesion studies as well as experiments that injected a barbiturate derivative (amytal) into one of the internal carotid arteries (to suppress the activity of one hemisphere) showed that the loss of activity in the left frontal cortex was associated with depressed affect, whereas loss of activity in the right frontal cortex was associated with manic affect and euphoria (Alema et al., 1961; Black, 1975; Gainotti, 1972; Gasparrini et al., 1978; Goldstein, 1939; Perria et al., 1961; Robinson & Price, 1982; Rossi & Rosadini, 1967; Sackeim et al., 1982; Terzian & Cecotto, 1959). These outcomes are likely due to the release of one hemisphere from contralateral inhibitory forces (Schutter & Harmon-Jones, 2013). For example, when the right hemisphere was deactivated by damage or amytal, the left hemisphere became more uninhibited and more active, which caused manic affect.
222 EDDIE HARMON-JONES, TAYLOR POPP, AND PHILIP A. GABLE
These results can be interpreted in one of two ways. According to the affective valence model of frontal asymmetry, the left frontal cortical region is involved in the experience and expression of positive affect, whereas the right frontal cortical region is involved in the experience and expression of negative affect. According to the motivational direction model of frontal asymmetry, the left frontal cortical region is involved in the experience and expression of approach motivation, whereas the right frontal cortical region is involved in the experience and expression of withdrawal motivation. Until the 1990s, the two conceptual models were considered to yield the same predictions because approach motivation was conceived of as being associated with positive affect and withdrawal motivation was conceived of as being associated with negative affect. In the late 1990s, researchers began using anger to tease predictions from these two conceptual models apart, because anger is an approach-motivated but negative affect (Harmon-Jones, 2003a). The following sections briefly review the research on the two models along with research on anger and frontal asymmetry.
# **11.3 Resting Asymmetric Frontal Activity and Trait Affective Valence**
These early results inspired EEG researchers to examine EEG alpha power over the frontal cortex and test whether it was associated with affective variables. Most of the first EEG studies on asymmetric frontal asymmetry tested individuals in a resting, baseline state (i.e., sitting quietly in the lab for four to eight minutes). Researchers assumed that this resting, baseline EEG would tap into a personality trait, and they then related EEG frontal asymmetry with other personality or individual difference measures.
Several studies found that depression was correlated with less relative left frontal cortical activity (e.g., Allen et al., 1993; Henriques & Davidson, 1990; Jacobs & Snyder, 1996; Schaffer et al., 1983; see meta-analysis by Thibodeau et al., 2006). Other studies suggested that trait negative affect was correlated with greater relative right frontal activity, whereas trait positive affect was correlated with greater relative left frontal activity (Tomarken et al., 1992).
# **11.4 Manipulations of Asymmetric Frontal Cortical Activity and Affective Reactions**
The studies assessing resting baseline asymmetric frontal cortical activity were correlational; therefore, it is impossible to infer that the differences in asymmetric frontal cortical activity were causally involved in the observed affective processes. In an effort ASYMMETRIC FRONTAL CORTICAL ACTIVITY 223
to provide evidence that would allow causal inferences, some researchers manipulated asymmetric frontal cortical activity and tested whether manipulation influenced other affective variables.
#### **11.4.1 Neurofeedback**
Studies have used neurofeedback training to manipulate asymmetric frontal cortical activity (e.g., Allen et al., 2001; Harmon-Jones et al., 2008). In this research, operant conditioning is used to produce certain patterns of brainwaves. Reward feedback (e.g., a simple tone) corresponding to "desired" patterns of brainwave activity is presented to participants. Over numerous presentations of this reward feedback, the brain learns to produce the desired brainwave activity, such as greater relative left frontal cortical activity. These neurofeedback-induced changes in brainwaves occur via nonconscious learning processes (Kamiya, 1979; Siniatchkin et al., 2000).
In one example experiment, relative right versus relative left frontal activity was manipulated using neurofeedback (Allen et al., 2001). In the experiment, participants were instructed to attempt to make a particular tone play as much as possible. Asymmetric frontal cortical activity (i.e., alpha power at F4 minus alpha power at F3) was calculated during the first second of each two-second time period. This calculated value was then compared against a criterion value that had been set for that session (based on the individual's previous asymmetry index). If the calculated value was larger than the criterion value in the desired direction, a "reward" tone was played; if it was not, a "non-reward" tone was played. After several days of neurofeedback training, participants then viewed emotionally evocative film clips as zygomatic and corrugator muscle region activity was recorded. Results revealed that the neurofeedback training influenced asymmetric frontal cortical activity in the predicted direction (for a replication, see Quaedflieg et al., 2016). Moreover, the manipulated increase in relative right frontal cortical activity, as compared to relative left frontal cortical activity, caused less zygomatic and more corrugator muscle region activity in response to all film clips. These results suggest that asymmetric frontal cortical activity is *causally* involved in emotional responses.
## **11.4.2 Unilateral hand contractions**
Asymmetric frontal cortical activity has also been manipulated using unilateral hand contractions. Because unilateral hand contractions cause increased activation of the contralateral motor region (Hellige, 1993), whose activation may spread to frontal regions, unilateral hand contractions may influence emotional responses (Schiff & Lamon, 1989; 1994). Indeed, research revealed that contractions of the left hand cause increased feelings of sadness and more negative perceptions and judgments, whereas 224 EDDIE HARMON-JONES, TAYLOR POPP, AND PHILIP A. GABLE
contractions of the right hand cause increased feelings of positive affect and more positive perceptions and judgments (Schiff & Lamon, 1989, 1994).
Based on this research, experiments have tested whether unilateral hand contractions would influence EEG and other emotional responses. In one experiment, participants were instructed to squeeze a ball in their left or right hand for several minutes (Harmon-Jones, 2006). Then, their self-reported affective responses were measured in response to a radio editorial designed to evoke a moderate amount of positive affect. Results revealed that the contraction of one hand increased cortical activity over the central and frontal regions of the contralateral hemisphere (as measured by EEG alpha suppression; see Gable et al., 2013 for replication). Moreover, this manipulation influenced positive affect, such that right-hand contractions caused more positive affect than the left-hand contractions.
## **11.4.3 Situational Manipulations of Positive and Negative Affect and Asymmetric Frontal Cortical Responses**
Additional research has measured asymmetric frontal cortical activity in response to manipulations of positive and negative affect. For example, Davidson and Fox (1982) found that 10-month-old infants evidenced greater relative left frontal cortical activity to film clips of an actress displaying happy facial expressions as compared to sad facial expressions. Ekman and Davidson (1993) found that adults evidenced greater relative left frontal activity when they were induced to make facial expressions of genuine smiles of joy as compared to facial expressions of non-genuine smiles of joy. Coan, Allen, and Harmon-Jones (2001) found that adults evidenced less relative left frontal activity when they were induced to make facial expressions of fear as compared to several other types of emotional facial expressions.
# **11.5 Asymmetric Frontal Cortical Activity and Motivational Direction**
Several studies suggest that the left frontal cortical region is involved in the experience and expression of positive affect, whereas the right frontal cortical region is involved in the experience and expression of negative affect. This research suggested that asymmetric frontal cortical activity reflected positive or negative affect, or affective valence. Research testing this affective valence model happened concurrently with other research testing a motivational direction model, which posits that relative left frontal cortical activity is associated with approach motivation and that relative right frontal cortical activity is associated with withdrawal motivation. For several years, the affective ASYMMETRIC FRONTAL CORTICAL ACTIVITY 225
valence and motivational direction models were viewed as compatible models that made identical predictions. This compatibility resulted from viewing positive affect as being always associated with approach motivation and negative affect as being always associated with withdrawal motivation.
## **11.5.1 Resting Asymmetric Frontal Activity and Trait Motivational Direction**
Many studies measured trait approach and withdrawal motivation with Carver and White's (1994) behavioral inhibition/behavioral activation system (BIS/BAS) questionnaires. The approach motivation (BAS) questionnaire has items such as "I go out of my way to get things I want" and "I crave excitement and new sensations". The withdrawal motivation (BIS) questionnaire has items such as "I worry about making mistakes" and "I have very few fears compared to my friends (reverse scored)."
The first two studies found that individual differences in self-reported trait approach motivation were correlated with greater relative left frontal cortical activity during resting baseline sessions (Harmon-Jones & Allen, 1997; Sutton & Davidson, 1997). One of these studies also found that trait "withdrawal" motivation correlated with greater relative right frontal activity during resting baseline (Sutton & Davidson, 1997), whereas the other study found no significant correlation between trait withdrawal motivation and relative right frontal activity (Harmon-Jones & Allen, 1997).
Additional studies replicated this latter pattern of results (Amodio et al., 2008; Amodio et al., 2004; Coan & Allen, 2003), and an EEG source localization study suggested that this trait approach/relative left frontal cortical activity correlation was due to activation in the middle frontal gyrus (BA11; De Pascalis et al., 2013).
## **11.5.2 Situational Manipulations of Motivation and Asymmetric Frontal Cortical Responses**
#### 11.5.2.1 *Pictures of Motivationally Significant Stimuli*
To test whether approach motivational intensity would predict relative left frontal cortical activity to appetitive stimuli, studies have been conducted that first measured individuals' self-reported liking for dessert and the time since they had last eaten. These measures were included to assess individual differences in approach motivation relevant to the stimuli to be presented. Next, participants viewed pictures of desserts and neutral objects while EEG was recorded. Results revealed that individuals with more intense approach motivation (i.e., longer time since eating, more liking for dessert) toward pictures of desserts evidenced more relative left frontal activity to dessert stimuli but not to neutral stimuli (Gable & Harmon-Jones, 2008; Harmon-Jones & Gable, 2009). In these studies, the appetitive pictures alone did not cause a significant increase 226 EDDIE HARMON-JONES, TAYLOR POPP, AND PHILIP A. GABLE
in relative left frontal cortical activity. This lack of a main effect of picture type on asymmetric frontal activity is consistent with some other research (Elgavish et al., 2003; Hagemann et al., 1998; see also reviews by Murphy et al., 2003 and Pizzagalli et al., 2003). The lack of a main effect may have occurred because pictures evoke different amounts of approach (withdrawal) motivation across participants. Some individuals may respond with no motivation, and others may respond with much motivation (Harmon-Jones, 2007).
Other research has suggested that some pictorial stimuli may evoke intense approach (or withdrawal) motivation in all participants. For example, Schöne and colleagues (2016) found that erotic stimuli caused greater relative left frontal activity than comparison stimuli of extreme sports, dressed women, and daily activities. The observed difference in relative left frontal activity between erotic and extreme sports stimuli is particularly interesting because both sets of stimuli evoked high and equal levels of selfreported positive affect and arousal.
#### 11.5.2.2 *Positive Affects Varying in Approach and Asymmetric Frontal Cortical Activity*
This research suggests that relative left frontal cortical activity reflects the intensity of approach motivation. However, most of this research could be interpreted by the valence model as well, which would simply posit that the results are due to positive affect instead of approach motivation. One way to tease these two conceptual models apart is to manipulate the intensity of approach motivation while holding positive affect constant. The motivational direction model would predict that positive affects high in approach motivation should evoke greater relative left frontal cortical activity than positive affects low in approach motivation. The affective valence model would instead predict that both types of positive affect should evoke equal levels of relative left frontal cortical activity.
One experiment tested these competing predictions by having individuals write about: 1) the steps needed to obtain a desired goal (positive action-oriented); 2) a normal day (neutral); or 3) a past event that made them feel good without personal action (positive inaction-oriented; Harmon-Jones et al., 2008, Experiment 2). The two positive conditions evoked greater levels of self-reported general positive affect than the neutral condition. However, the positive action-oriented condition caused greater relative left frontal cortical activity than the other two conditions did. Thus, these results suggest that high approach-motivated positive affect caused greater relative left frontal cortical activity than low approach-motivated positive affect.
#### 11.5.2.3 *Facial Expressions of Approach-Motivated Positive Affect*
Based on research that had revealed that facial expressions of determination were identified as being high in positive approach motivation (Harmon-Jones et al., 2011), subsequent research instructed individuals to make a facial expression that expressed "determination" or a low approach-motivated positive expression of "satisfaction" or a neutral expression (Price et al., 2013). Then, individuals performed a task that ASYMMETRIC FRONTAL CORTICAL ACTIVITY 227
assessed behavioral persistence. As predicted by the motivational model (but not the affective valence model), individuals who made the determination facial expression (high approach-motivated positive affect) had greater relative left frontal activity than individuals in the other two conditions. In addition, within the determination condition, greater relative left frontal cortical activity was associated with greater behavioral persistence.
### 11.5.2.4 *Using Whole Body Posture to Manipulate Approach Motivation*
Based on previous research that had shown that whole body posture can manipulate levels of approach motivation (e.g., Harmon-Jones & Peterson, 2009; Price & Harmon-Jones, 2011), research was conducted to test whether this manipulation would influence relative left frontal cortical activity. In this study, seated individuals were instructed to either lean forward as one might do while reaching for a desired object (high approach) or to recline fully in a reclining chair (low approach; Harmon-Jones et al., 2011). Then, while in one of these two positions, the individuals viewed approach-oriented (dessert) and neutral (rock) pictures using virtual reality glasses, so that the viewing distance was held constant. As predicted, individuals in the high approach leaning forward posture evidenced greater relative left frontal activity to the approach-oriented stimuli as compared to the neutral stimuli. Individuals in the low approach reclining posture did not evidence a difference in relative left frontal activity to the two picture types.
## 11.5.2.5 *Final Thoughts*
The reviewed evidence suggests that relative left frontal cortical activity is associated with approach motivation. This association occurs even when approach motivation is not confounded with positive affect. That is, in approach motivation, some positive affects are low and some are high, but the research has revealed that it is primarily the high approach-motivated positive affects that are associated with greater relative left frontal activity.
# **11.6 Anger and Asymmetric Frontal Cortical Activity**
To better understand the emotive functions of asymmetric frontal cortical activity, anger has been examined, as anger provides a way of removing the "natural" confound between affective valence and motivational direction. That is, anger is often posited to be a negative affect (Harmon-Jones, 2004; Harmon-Jones et al., 2011) associated with approach motivation, as recognized in classic work (e.g., Darwin, 1872; Blanchard & Blanchard, 1984; Ekman & Friesen, 1975; Lagerspetz, 1969; Plutchik, 1980; Young, 1943) as well as more contemporary work (e.g., Berkowitz & Harmon-Jones, 2004; 228 EDDIE HARMON-JONES, TAYLOR POPP, AND PHILIP A. GABLE
Carver & Harmon-Jones, 2009; Harmon-Jones et al., 2009; Harmon-Jones et al., 2013). To give just a few examples, research has revealed that individual differences in BAS (Carver & White, 1994) are positively correlated with individual differences in anger (Harmon-Jones, 2003b; Smits & Kuppens, 2005), greater anger responses to situational anger manipulations (Carver, 2004), greater aggressive inclinations especially when approach motivation is activated (Harmon-Jones & Peterson, 2008), and more attentional engagement to angry faces, as in approach-based dominance confrontations (Putman et al., 2004).
If asymmetric frontal cortical activity reflects affective valence, then anger should be associated with relative right frontal activity because anger is a negative affect. In contrast, if asymmetric frontal cortical activity reflects motivational direction, then anger should be associated with relative left frontal activity because anger is approach motivated. Research has tested these competing predictions.
## **11.6.1 Resting Asymmetric Frontal Cortical Activity and Trait Anger**
Studies with adolescents (Harmon-Jones & Allen, 1998) and young adults (Harmon-Jones, 2004) have found that individual differences in anger relate positively with relative left frontal cortical activity, assessed during resting baseline. This latter study also measured attitudes toward anger and revealed that anger was regarded as a negative affect and that these negative attitudes toward anger did not correlate with asymmetric frontal activity. Other studies have revealed that trait anger correlates positively with relative left frontal activity in incarcerated violent offenders (Keune et al., 2012), and that trait aggression correlates positively with relative left frontal activity in adults with ADHD (Keune et al., 2011). Following from research showing that anger and jealousy are positively correlated in some circumstances, research has revealed that one-year-old infants with greater relative left frontal activity during a resting baseline display more jealous responses when their mothers attend to a social rival (Mize & Jones, 2012).
## **11.6.2 Manipulation of Asymmetric Frontal Cortical Activity and Anger Reactions**
Other research has tested whether the manipulation of asymmetric frontal cortical activity via unilateral hand contractions will influence anger-related responses. In one experiment, participants contracted their right or left hand using the methods described earlier (Harmon-Jones, 2006). Then, they received insulting interpersonal feedback and then played a reaction time game against the person who had ostensibly insulted them. The reaction time game provided an assessment of behavioral aggression, as participants could select the volume and duration of noise blast to give ASYMMETRIC FRONTAL CORTICAL ACTIVITY 229
to the other participants on trials they won. Replicating previous research, the contraction of the right hand led to greater relative left central and frontal cortical activity than the contraction of left hand. More importantly, as compared to the left hand contractions, the right hand contractions led to more aggression behavior (Peterson et al., 2008).
Additional research revealed that compared to left-hand contractions, righthand contractions led to greater self-reported anger to being socially ostracized in a Cyberball game (Peterson et al., 2011). These results suggest that manipulated increases in relative left frontal cortical activity lead to increased anger-related responses.
#### **11.6.3 State Anger and Relative Left Frontal Cortical Activity**
Other research has tested whether situationally manipulated anger influences relative left frontal cortical activity. In one experiment, participants who were insulted (i.e., received insulting feedback on an essay they had written) responded with greater relative left frontal activity than individuals who were not insulted (i.e., received mildly positive feedback; Harmon-Jones & Sigelman, 2001). Moreover, within the insult condition, self-reported anger to the feedback and behavioral aggression toward the person who provided the feedback were both positively correlated with relative left frontal activity. Other experiments have conceptually replicated these results (e.g., Harmon-Jones et al., 2004; Jensen-Campbell et al., 2007; Verona et al., 2009). Research has extended these early results by showing that lab-induced social rejections can induce feelings of jealousy and anger as well as increased relative left frontal cortical activity (Harmon-Jones et al., 2009).
Individual differences have also been found to moderate these anger-related relative left frontal cortical activity responses. For instance, one study found that, as compared to individuals with no affective disorders, individuals with borderline personality disorder had greater relative left frontal activity to social rejection, whereas individuals with major depression had greater relative right frontal activity to social rejection (Beeney et al., 2014). In addition, individual differences in BAS positively correlated with greater relative left frontal cortical activity to anger induced via pictures offensive to the sample of individuals (Americans viewing anti-American images such as flag burning; Gable & Poole, 2014).
## **11.6.4 Manipulating Approach Motivation Independently of Anger**
Anger is presumably related to relative left frontal cortical activity because anger is associated with approach motivation. Even more compelling evidence for the 230 EDDIE HARMON-JONES, TAYLOR POPP, AND PHILIP A. GABLE
association between approach motivation and relative left frontal cortical activity could be provided by manipulating approach motivation independent of anger. That is, even though anger is often approach motivated, anger is not perfectly associated with approach motivation and thus it should be possible to manipulate the two constructs separately.
For example, one variable that should influence (approach) motivational intensity is coping potential or the difficulty of engaging in behavior. That is, motivational intensity increases with perceived task difficulty up to the point where the task is perceived as impossible, and then motivational intensity drops. So, when a task is perceived as impossible, or coping potential is very low, motivational intensity should be low (Brehm, 1999; Brehm & Self, 1989).
In one experiment testing these hypotheses, individuals were induced to believe that they would or would not be able to engage in action that might resolve the angerevoking event (i.e., sign petitions to halt a university tuition increase; Harmon-Jones et al., 2003). Results revealed that individuals who were angered and believed they could engage in action had greater relative left frontal activity than individuals who were angered and believed they could not engage in action (the tuition increase had already been approved). Moreover, in the action-possible condition, greater relative left frontal activity in response to the angering event correlated with more approach-related behavior (i.e., signing the petition and taking more petitions to have others sign). Other studies have conceptually replicated this effect of anger and approach action possibility on relative left frontal activity using pictorial stimuli to evoke anger (Harmon-Jones et al., 2006).
These results could be interpreted to indicate that greater relative left frontal cortical activity only occurs to anger evocations when individuals are given explicit approach motivational opportunities. Other research suggests, however, that these explicit approach motivational opportunities increase relative left frontal activity but are not necessary for it to occur. That is, individuals who were exposed to pictures that evoked anger and were given no explicit approach opportunities had increased relative left frontal cortical activity if they were high in trait anger (Harmon-Jones, 2007). Thus, explicit opportunities for approach-motivated behavior are not necessary to cause relative left frontal activity during anger. Anger can evoke approach motivation without explicit approach motivational opportunities being immediately present.
Other experiments have manipulated approach motivation independently of anger and found that the approach motivation drives the increase in relative left frontal activity. For example, one experiment used a manipulation of whole-body posture to manipulate approach motivation. When individuals are in a supine body position (lying flat on their backs), they are likely to be less approach motivated. In this anger experiment, individuals were interpersonally insulted while sitting upright or while in a supine posture. Results revealed that individuals who were insulted while in the supine posture had lower relative left frontal cortical activity than individuals who were insulted while sitting upright (and the latter condition had greater relative left frontal activity than an ASYMMETRIC FRONTAL CORTICAL ACTIVITY 231
upright-neutral-no-insult comparison condition; Harmon-Jones & Peterson, 2009). Interestingly, the results also revealed that both the supine and upright insult conditions reported feeling angrier than the neutral comparison condition, and these two insult conditions did not differ from each other. Thus, this research suggests that anger relates to relative left frontal cortical activity because of approach motivation; when approach motivation was decreased with a supine body posture, individuals who were angered did not have the typical increase in relative left frontal activity. However, they did have the same level of angry feelings as those who were in the standard upright insult condition, suggesting that angry feelings are not inevitably associated with relative left frontal activity or approach motivation.
## **11.6.5 Anger and Avoidance Motivation**
A correlational study (Hewig et al., 2004) measured trait anger-out, trait anger-in, and trait anger-control using the State-Trait Anger Expression Questionnaire (Spielberger, 1988). Resting baseline asymmetric frontal cortical activity was also assessed. Trait anger-out likely measures approach-motivated anger (e.g., "When angry or furious, I lose my temper"; Spielberger et al., 1995, p. 57). Trait anger-in measures the extent to which individuals hold anger in (e.g., "When angry or furious, I keep things in"). Trait anger-control measures the extent to which individuals control their anger (e.g., "When angry or furious, I control my angry feelings."). Trait anger-out correlated with greater relative left frontal activity. Trait anger-control correlated with greater relative right frontal activity. Trait anger-in was not significantly correlated with asymmetric frontal cortical activity. The researchers suggested that anger-control was associated with relative right frontal activity because anger-control was associated with anger withdrawal.
Anger may evoke withdrawal when anger is mixed with concerns about being punished. For example, some individuals may become angry over social policies that pressure one to behave less racially prejudiced. At the same time, however, they may experience anxiety about expressing anger in these situations because they fear social censure. A study designed such a situation in the lab and found that anger in this situation was associated with greater relative right frontal cortical activity (Zinner et al., 2008). In this study, anger in response to the situation correlated with more spontaneous eye blinking, suggesting that anger was also associated with suppressing emotions (Gross & Levenson, 1993). Moreover, self-reported anger was associated with self-reported anxiety. These latter results support the idea that the social situation had also evoked concerns about being socially censured for feeling angry. Although these results are correlational, the authors suggest that anger may be associated with relative right frontal cortical activity when the motivation to withdraw is also high.
232 EDDIE HARMON-JONES, TAYLOR POPP, AND PHILIP A. GABLE
# **11.7 Effortful Control and Relative Right Frontal Activity**
As noted, models of frontal asymmetry link approach motivation with greater relative left frontal activity. Both the affective valence model and the motivational direction model of frontal asymmetry associate withdrawal motivation with greater relative right frontal activity. Despite evidence supporting this model, many studies have failed to replicate the relationship between right frontal activity and withdrawal motivated traits and states (Amodio et al., 2008; Berkman & Lieberman, 2010; Coan & Allen, 2003; Coan et al., 2001; De Pascalis et al., 2013; Henriques & Davidson, 2000; Hewig et al., 2004, 2006; Jackson et al., 2003; Keune et al., 2012; Kline et al., 2000; Pizzagalli et al., 2005; Quirin et al., 2013; Wacker et al., 2008; Wacker et al., 2010). This has led researchers to question what could be causing the inconsistencies in the literature. Some suggest that withdrawal motivation is a complex system that is difficult to accurately measure independently of confounding variables (Amodio et al., 2008; Coan & Allen, 2004). Others suggest that another system entirely accounts for greater right frontal asymmetry.
A model presented by Gable and colleagues (2018) suggested that right frontal activity is more related to regulatory control than to withdrawal motivation. Regulatory control is thought to be carried out by the revised BIS (r-BIS; Gray & McNaughton, 2000), which may act as a governing body over conflicts between the approach and withdrawal systems. Activation of r-BIS leads to enhanced attention to, memory for, and detection of negatively valenced information, allowing it to manage conflicts by enhancing aversion to one motivated behavior over the other (Heym et al., 2008). This can occur as either the suppression of a behavioral response or an override of motivational impulses (Aron et al., 2004, 2014; Carver & Connor-Smith, 2010; Hester & Garavan, 2004, 2009). As such, r-BIS is related to effortful control, constraint, self-control, inhibition, conflict monitoring, and error detection (Carver & Connor-Smith, 2010; Carver et al., 2008; Derryberry & Rothbart, 1997; Gray & McNaughton, 2000; Kochanska & Knaack, 2003; Nigg, 2006; Rothbart & Rueda, 2005). Low functioning r-BIS is thought to be related to impulsive behavior, deficits in inhibitory control, and externalizing disorders such as substance abuse (Enticott et al., 2006; Logan et al., 1997). Unusually high functioning of r-BIS, on the other hand, may be related to passive avoidance, anxious inaction, and internalizing disorders such as generalized anxiety disorder (Carver et al., 2008; DeYoung, 2015; Eisenberg et al., 2004; Rothbart et al., 2004; Strack & Deutsch, 2004; Valiente et al., 2003).
While much research has examined the relationship between asymmetric frontal cortical activity and motivational systems, few studies have investigated the connections between regulatory control (r-BIS) and asymmetric frontal activity (Gable et al., 2015; Grimshaw & Carmel, 2014; Neal & Gable, 2016; Wacker et al., 2003). R-BIS acts as a controlling agent over approach and withdrawal behaviors. The present model suggests ASYMMETRIC FRONTAL CORTICAL ACTIVITY 233
that greater relative right frontal activity is indicative of greater r-BIS functioning whereas reduced relative right frontal activity suggests reduced r-BIS functioning.
#### **11.7.1 Trait r-BIS and Frontal EEG Activity**
R-BIS functioning is a stable individual difference measured via personality questionnaires targeting traits such as impulsivity, sensation seeking, and inhibition. When r-BIS is hyperactive, traits such as neuroticism and anxiety caused by passive avoidance become prevalent, often resulting from approach-avoidant conflicts (DeYoung, 2015). When r-BIS is hypoactive, on the other hand, approach and withdrawal may be unregulated and individuals may be less able to inhibit motivational tendencies. Impulsivity is thought to index inverse functioning of r-BIS because r-BIS is strongly related to inhibition, effortful control, and overall executive functioning (Bari & Robbins, 2013; Bickel et al., 2012; Eisenberg et al., 2004).
Impulsivity can be measured with a number of personality traits. For instance, positive urgency measures impulsivity through the failure of r-BIS to inhibit approach tendencies, which ultimately leads to rash action during intense positive states (Cyders et al., 2010; Zapolski et al., 2009). To examine relationships between impulsive personality traits and asymmetrical frontal cortical activity, Gable and colleagues (2015) conducted a resting frontal EEG study investigating the association between positive urgency and frontal activity. Results showed a relationship between positive urgency and greater relative left frontal activity. This suggests that reduced relative right frontal activity is associated with reduced r-BIS function. Using standardized low-resolution brain electromagnetic tomography (SLORETA; Pascual-Marqui, 2002), source localization results indicated that lower relative right frontal activity was due to reduced activity in the right inferior frontal gyrus (rIFG). This further suggests that it is reduced right frontal activity, rather than increased left frontal activity, that was driving the observed asymmetric activity.
Neal and Gable (2016) investigated the relationship between frontal activity and tenets of impulsivity that are not related to positive affect or approach motivation. Participants completed the UPPS-P scale, which assesses negative urgency, lack of premeditation, and lack of perseverance, along with positive urgency (Cyders & Smith, 2007; Whiteside et al., 2005). Participants' resting EEG activity was then assessed. Negative urgency (i.e., rash behavior in negative emotional contexts) was related to heightened left frontal activity at rest, suggesting that the relationship between impulsivity and relative left frontal activity was not driven by positive emotionality. Non-emotional impulsive traits (i.e., lack of premeditation and lack of perseverance) were also associated with reduced right frontal activity. This relationship between impulsivity and right frontal activity remained unchanged when controlling for trait approach motivation. Source localization for the relationship between these tenets of impulsivity showed reduced activity in the right cingulate gyrus and the right medial frontal gyrus. Taken together, these 234 EDDIE HARMON-JONES, TAYLOR POPP, AND PHILIP A. GABLE
results suggest that impulsivity is associated with reduced right frontal activity, independent of affective valence.
This study did not find a relationship between trait sensation seeking and frontal activity. However, the type of sensation seeking scale used (UPPS-P measure of trait sensation seeking) does not correlate well with other subscales of the UPPS-P, and some researchers have suggested that it may reflect a construct other than impulsivity (Simons et al., 2010). Santesso et al. (2008), however, used the Zuckerman Sensation Seeking Scale to measure trait sensation seeking and found that it was related to greater left frontal (reduced right frontal) activity.
Overall, these findings suggest that deficits in persistence and inhibiting behavior are associated with reduced right frontal activity. Source localization of the relationship between r-BIS and frontal asymmetry suggests that the asymmetry is driven by reduced activity in the right medial and lateral frontal areas, including areas of the right prefrontal cortex.
## **11.7.2 Evidence of r-BIS Functioning in Frontal EEG Activity**
Source localization studies have also investigated the source of activity relating to behavioral measures of control. Gianotti and colleagues (2009) collected resting EEG data before having participants engage in a behavioral risk task. When participants engaged in greater risk-taking behavior, activity was localized to diminished baseline activity in the right lateral prefrontal cortex. Those whose resting activation of the right prefrontal cortex was less stable demonstrated less supervisory control of risky behavior. In a later study, resting EEG activity was compared to participants' subsequent acceptance of unfair offers in the ultimatum game (Knoch et al., 2010). When presented with an unfair offer, participants could either accept the offer or punish the opponent for giving them the offer. Acceptance of unfair offers was assumed to reflect an ability to exercise control over the initial emotional response in order to maximize economic benefits. Results showed a positive correlation between baseline right frontal activity and increased acceptance of most unfair offers. This activity was also localized to the right lateral prefrontal cortex.
Studies investigating regulation of anger have demonstrated that effortful control of anger relates to greater right frontal activity. Hewig and colleagues (2004) found that the extent to which individuals control their anger (State-Trait Anger Expression Questionnaire; Spielberger, 1988) related to greater relative right frontal asymmetry during resting baseline. The researchers suggested that anger-control was associated with relative right frontal activity because anger-control was associated with anger withdrawal, but based on the evidence, it seems likely that greater right frontal activity is linked with greater anger-control because it is associated with greater effortful control. Other work has demonstrated that suppressing anger, when it is socially inappropriate ASYMMETRIC FRONTAL CORTICAL ACTIVITY 235
to express it, causes greater right frontal activity (Zinner et al., 2008). Although greater right frontal activity may be associated with the motivation to withdraw in some anger states, these results also support that greater right frontal activity is associated with effortful control stemming from emotional suppression of anger.
Functioning of r-BIS can also be connected to drug and alcohol reactivity. Greater relative left frontal (reduced right frontal) activity has been connected to drug-cue reactivity such as alcohol exposure (Myrick et al., 2004) and cocaine cravings (van de Laar et al., 2004). These increases in left frontal activity in response to substance cues are thought to be indicative of appetitive responses evoked from substancerelated stimuli (Carter & Tiffany, 1999). Hypoactivation of rBIS, however, can also cause increased responsiveness toward alcohol. Mechin and colleagues (2016) investigated whether it is trait impulsivity or trait approach motivation that drives the increase in relative left frontal activity in response to alcohol-related cues. To determine this, they had participants complete the UPPS-P Behavioral Impulsivity Scale (Cyders & Smith, 2007; Whiteside et al., 2005), the BIS/BAS scales (Carver & White, 1994), and questions about their drinking habits. They then collected EEG data while participants viewed alcohol-related and neutral picture cues. Results suggested that the reduction in right frontal activity toward alcohol cues was due to trait impulsivity rather than trait approach motivation. The relationship between impulsivity and alcohol picture presentation remained constant when controlling for drinking behaviors and asymmetric frontal activity in response to neutral pictures. These results suggest that r-BIS moderates asymmetric frontal activity to alcohol cues while BAS does not.
Impulsivity is presumably related to relative right frontal cortical activity because impulsivity is associated with reduced effortful control. Evidence demonstrating increases in relative right frontal activity when individuals demonstrate greater effortful control and increases in relative left frontal activity when individuals demonstrate greater impulsivity could provide more compelling evidence for this model. Neal and Gable (2019) used a Balloon Analogue Risk Task (BART) to test whether impulsive or controlled behaviors influence asymmetric frontal activity. In this study, EEG recordings were collected as participants performed the BART while simultaneously viewing alcohol stimuli designed to enhance impulsive tendencies. Participants could win money by successfully blowing up a virtual balloon. With each pump of the balloon, more money could be won, but the likelihood of the balloon popping increased. Each trial ended with either the participant cashing out on the balloon or the balloon popping.
EEG data collected during this task showed that asymmetry scores shifted throughout alcohol trials. Frontal activity would shift to greater relative left frontal activity in the last half of trials where the balloon popped (impulsive behavior) while activity would shift to the right on the last half of trials where the participant cashed out (successful inhibition). These shifts were localized to reduced activity in the rIFG and lIFG, respectively. This suggests that increased right frontal activity is indicative of impulse control and diminished right frontal activity leads to more impulsive behavior.
236 EDDIE HARMON-JONES, TAYLOR POPP, AND PHILIP A. GABLE
The right frontal cortex has also been found to play an important role in the r-BIS functions of error detection, emotion regulation, and self-control. When an incorrect or inappropriate behavior is enacted, the error-related negativity (ERN) is evoked in response. Individuals with greater levels of behavioral inhibition, anxiety, and emotion regulation tend to have increased ERN amplitudes, suggesting that those with higher functioning r-BIS show greater neural responses in response to conflict monitoring (Amodio et al., 2008; Proudfit et al., 2013; Teper & Inzlicht, 2013). Greater relative right frontal activity at baseline has been linked to increased ERN amplitudes, while greater relative left frontal activity has been linked to reduced ERNs (Nash et al., 2012). Taken together, these results suggest that greater relative right frontal activity is related to greater r-BIS functioning in terms of conflict detection in response to errors.
Recently, Lacey and colleagues (2020) further connected emotion regulation to right frontal activity. In one experiment, participants listened to anxiety-inducing and neutral sound clips and were told to either listen naturally or suppress their emotional reactions to the clips. Participants recorded their level of effort when suppressing their reactions and noted their affective experience on each trial. Results showed that, when participants recorded higher levels of effortful control, right frontal activity was increased. However, experience of negative emotion was not associated with this increase in right frontal activity. In a second experiment, participants were shown negative and neutral pictures and told that looking at the images for a long time would earn them money, while choosing to escape from looking at the pictures would earn them no reward. In this study, right frontal activity was associated with looking at negative pictures for a longer time during reward trials, but not during non-reward trials. Both studies indicate that it was not the negative affect associated with the aversive stimuli, but rather the effort to engage the negative stimuli that was related to an increase in right frontal activity.
Schmeichel and colleagues (2016) evaluated the relationship between self-control and asymmetrical frontal activity. In this study, participants either had their selfcontrol depleted or not, and then underwent EEG recording while viewing positive pictures. Among individuals who were relatively higher in trait BAS than BIS, those with depleted (vs. non-depleted) self-control showed increased left frontal activity in response to positive pictures. Among those with no relative difference in BIS and BAS scores, those with depleted self-control showed decreased left frontal activity in response to positive pictures. This suggests that when r-BIS is depleted, those who generally exhibit more approach motivation show greater left frontal activity in response to rewarding stimuli. An enhanced r-BIS, on the other hand, may be able to lower approach motivation in those with generally hyperactive BAS and hypoactive BIS.
Overall, these studies suggest that greater right frontal activity may be associated with processes involving emotion regulation while lower right frontal activity may be associated with reduced self-control and hindered error monitoring. Additionally, both ASYMMETRIC FRONTAL CORTICAL ACTIVITY 237
situational contexts where control must be utilized and control-related personality traits have been related to right frontal activity as measured with EEG.
# **11.8 Additional Models of Frontal Asymmetry**
Researchers have presented additional models to explain frontal asymmetry and its relationship to emotional and motivational variables. The Bilateral BAS Model (Hewig et al, 2004) and the Activation vs. Inhibition Model (Wacker et al., 2003) each propose variants of how approach, withdrawal, and inhibition influences frontal asymmetry.
#### **11.8.1 Bilateral BAS Model**
Hewig's bilateral BAS model suggests that both the approach and withdrawal systems encompass the basic mechanisms of active behavior and are therefore both subsystems of the BAS. When active behavior is initiated, then, bilateral activation of the frontal cortices is expected. Hewig and colleagues (2004) first addressed the model in their study analyzing resting frontal alpha band asymmetry and its relationships with affective valence, motivational direction, and behavioral activation. Resting state data obtained from each participant was related to measures of trait anger and different anger styles (STAXI, Spielberger, 1988), affective valence (PANAS), aggression (Aggression Questionnaire), and behavioral activation (BIS/BAS). Data analyses indicated that while valence was not significantly related to frontal asymmetry, relative left frontal cortical activity was positively correlated with outwardly expressed anger ("angerout," Spielberger, 1988), trait anger, and aggression, while relative right frontal cortical activity was positively correlated with lowering arousal in anger-inducing situations ("anger-control," Spielberger, 1988). Additionally, greater bilateral frontal cortical activity was associated specifically with higher BAS scores. These results together suggest that greater levels of frontal asymmetry are driven by motivational tendencies and that bilateral frontal activation is driven by the combination of the approach and withdrawal subsystems of the BAS. A later study (Hewig et al., 2006) using similar methods found comparable results. Those participants who showed greater bilateral activation while in a resting state had higher BAS scores. The authors suggest that this result indicates that BAS scores may encompass both approach- and withdrawal-motivated behaviors.
In 2006, Hewig and colleagues conducted a go/no-go experiment to discern the relationship between positive and negative reinforcement and BAS scores. In this study, participants were first shown a cue indicating whether success on the given trial could add to the participant's money (positive reinforcement) or stop money from being subtracted (negative reinforcement). According to Gray's model of BIS/BAS (e.g., 1982), 238 EDDIE HARMON-JONES, TAYLOR POPP, AND PHILIP A. GABLE
both types of reinforcement should activate the BAS, as both are a form of reward or non-punishment. Participants then completed a go/no-go task in which no-go trials were considered to be a form of passive avoidance, therefore activating the BIS. After the task, participants were shown monetary feedback based on their performance. Results showed that all participants showed greater bilateral frontal activation in response to reinforcement trials—regardless of whether it was positive or negative reinforcement and that this effect was strongest in those with higher trait BAS scores. When these results are considered with prior research suggesting that approach motivation aligns with greater relative left frontal activity and withdrawal motivation aligns with greater relative right frontal activity, the suggestion is that the two are subsystems of the overarching BAS, once again supporting Hewig and colleagues' bilateral BAS model.
Rodrigues and colleagues (2018) found further support for the bilateral BAS model using a virtual reality paradigm. In this study, participants navigated a virtual T maze in which they were to respond to various events. These events could be positive, negative, or neutral in valence. Positive trials encouraged participants to move toward the event while negative trials encouraged withdrawal from the event. Approach-avoidance conflict trials involved having a positive stimulus guarded by a negative stimulus and approach-approach conflict trials involved choosing between two positive stimuli. There were also two control trial types. In each trial, participants chose in which direction they would like to move while EEG was recorded. Left frontal activity increased when participants chose an approach direction while right frontal activity increased when participants chose a withdrawal direction. Further, bilateral frontal activity increased during any choice in behavior relative to the choice to not move in any direction. The authors argue that these results support the role of frontal asymmetry in behavioral approach or avoidance motivation, as well as the role of bilateral frontal activation in active behavior.
#### **11.8.2 Activation vs. Inhibition Model**
Wacker and colleagues (Wacker et al., 2003; Wacker et al., 2008, 2010) suggest that the driving force behind frontal asymmetry is whether any motivational system is being activated or inhibited. Consistent with Gray's revised behavioral inhibition system/ behavioral activation system (BIS/BAS) model (Gray & McNaughton, 2000), BAS is activated in response to approach motivation and rewarding stimuli, whereas the fight-flight-freeze system (FFFS) responds to withdrawal motivation and aversive stimuli. BIS responds to conflict between these two systems, acting as conflict monitor, shifting attention to allow for more efficient goal direction in conflicting situations (i.e., situations with more than one appetitive goal or a goal that requires combating aversive obstacles). Wacker and colleagues argue that all forms of behavioral activation are controlled by BAS and FFFS and are associated with greater relative left frontal activation, whereas behavioral inhibition and conflict monitoring are controlled by BIS and are associated with greater relative right frontal activation.
ASYMMETRIC FRONTAL CORTICAL ACTIVITY 239
In an early study, Wacker and colleagues (2003) compared the viability of the BIS/ BAS, motivational direction, and valence models of frontal asymmetry. Participants completed a mental image script task in which emotion (fear vs. anger) and motivation (approach vs. withdrawal) were manipulated and the participants reported the degree to which they agreed that the outcome of each task was the best option (degree of conflict). Results did not fall in line with the predictions of either the motivational direction or valence models of anterior asymmetry, but the degree of conflict experienced by participants was positively correlated with relative right frontal activation. Assuming that agreement ratings were a valid measure of BIS activation, these results support the model of frontal asymmetry suggested by Wacker and colleagues.
Similar results were found in a later study by Wacker and colleagues (2008), which directly compared the BIS/BAS model of anterior activation (BBMAA) to the motivational direction model. During a mental image script task similar to that used by Wacker and colleagues (2003), participants showed greater relative right frontal activation in response to scripts designed to target BIS than to those targeting FFFS. Selfreported measures of FFFS activation, conversely, were associated with greater relative left frontal activation.
The relationship between trait BIS and frontal asymmetry was investigated by Wacker and colleagues (2010) via a go/no-go task. Such a paradigm was used because no-go tasks have been suggested to be a viable measure of the conflict and behavioral inhibition functions of Wacker's revised BIS. Consistent with this assumption, those participants who had greater trait BIS showed greater relative right frontal activation in response to no-go trials than to go trials.
# **11.9 Psychopathology and Frontal Asymmetry**
Because frontal alpha asymmetry plays a role in the experience of motivation and emotion, it follows that it would also factor into the experience of mental illness, particularly mood disorders. The psychological conditions most frequently investigated in relation to frontal asymmetry are depression, anxiety, and bipolar disorder.
#### **11.9.1 Depression**
Depression is one of the most commonly studied conditions in relation to frontal asymmetry. Depressive symptomology includes experiences such as decreased response to reward, lack of positive affect, and greater tendencies toward withdrawal from triggering activities. Davidson and colleagues (2002) pointed out that these symptoms can often be described as deficiencies in approach motivation and hyperactive withdrawal motivation, and these trends are associated with decreased relative left frontal cortical activity 240 EDDIE HARMON-JONES, TAYLOR POPP, AND PHILIP A. GABLE
(greater relative right frontal activity). A number of studies have found a relationship between depressive symptoms and reduced left-frontal activity during a resting state. For instance, Schaffer and colleagues (1983) found a negative correlation between scores on the Beck Depression Inventory (BDI) and relative left frontal activity. Subsequent studies have found similar relationships between relative left frontal activity at rest and self-reported (Diego et al., 2001) or clinically diagnosed depression (Henriques & Davidson, 1990; Smith et al., 2018; Stewart et al., 2010). Henriques and Davidson (1990) even found that participants who had previously been depressed showed lower relative left frontal activity at rest compared to those who had never been depressed, and that these patterns of asymmetry were comparable to those in participants experiencing acute depressive symptoms. These results suggest that frontal asymmetry may be a stateindependent marker of depression.
It is of note that diminished relative left frontal activity in depressed individuals is particularly robust in women compared to men (Stewart et al., 2010). Stewart and Allen (2018) found evidence supporting this notion in a sample with no history of major depressive disorder. Participants engaged in resting state EEG recordings before returning one year later to report depressive symptomology during the worst two-week period experienced throughout the one-year interim. It was found that women—but not men—with lower relative left frontal activity at baseline reported greater degrees of depressive symptomology during the interim period.
While resting data provides a means of studying the relationship between frontal asymmetry and depression, some studies have found a null relationship between depression and frontal asymmetry (Harmon-Jones et al., 2002; Metzger et al., 2004; Tomarken & Davidson, 1994; McFarland et al., 2006). These null results have led some researchers to argue that state-measures of frontal asymmetry may be more reliably associated with depression. For example, the capability model of frontal asymmetry suggests that cortical activity measured during emotional challenges is more indicative of predispositions toward psychopathology than cortical activity measured at rest (Stewart et al., 2014). Lower relative left frontal activity during a facial emotion task was found to be indicative of a history of major depressive disorder (Stewart et al., 2011). Participants prone to depressive symptomology have also exhibited lower relative left frontal activity during tasks that evoke anger (Harmon-Jones et al., 2002) and sadness (Nitschke et al., 2004). Those with early-onset depression also exhibited lower relative left frontal activity during an approach-related reward paradigm (Shankman et al., 2007).
Frontal asymmetry may act as more of a risk factor than an indicator of current depression. In one study, Possel and colleagues (2008) measured resting frontal asymmetry in adolescent boys and related it to depressive symptoms experienced throughout the year following the EEG recording. Results suggested that lower baseline left frontal activity was predictive of melancholic depressive symptoms and increased right frontal activity was predictive of non-melancholic depressive symptoms one year later, but depressive state was not predictive of baseline asymmetry. This suggests that frontal asymmetry may be indicative of a predisposition to depression. Mitchell and Possel (2012) conducted a similar study comparing depression and resting asymmetry in a ASYMMETRIC FRONTAL CORTICAL ACTIVITY 241
nonclinical population and found that individuals with lower baseline left frontal activity were more likely to develop depressive symptoms over the next year. Nusslock and colleagues' (2011) results echoed these findings, suggesting that cognitive vulnerability to depression was both associated with lower relative left frontal activity at baseline and predicted onset of depressive symptoms one year later.
In addition, frontal asymmetry has been found to be a predictor of treatment response in depressed individuals. Greater relative left frontal activity prior to treatment predicted more successful response to fluoxetine (Bruder et al., 2001), as well as to escitalopram and sertraline in women (Arns et al., 2015).
#### **11.9.2 Anxiety**
Anxiety symptoms also appear to be related to greater right frontal activity. In a sample of participants consisting of healthy controls, those with major depression in remission, those with acute depression without comorbid anxiety disorder, and those with acute depression with a comorbid anxiety disorder, the only group difference observed was greater relative right frontal activity in the group with both major depression and a comorbid anxiety disorder compared to healthy controls (Feldmann et al., 2018). Other findings suggested that those with both anxiety and depression show frontal asymmetry patterns similar to those with depression alone (Mathersul et al., 2008). Nusslock and colleagues (2018) found asymmetry patterns to be most similar between healthy controls and those with comorbid depression and anxiety. In this study, women with a history of childhood onset depression without anxiety diagnoses showed reduced left frontal activity, which is consistent with past research on depression. However, women with a history of childhood onset depression and with pathological levels of anxious apprehension (in the form of generalized anxiety disorder, obsessive compulsive disorder, or separation anxiety disorder) showed resting asymmetry patterns statistically indistinguishable from healthy controls. These results highlight the role of comorbid depression and anxiety in its complex relationship with frontal asymmetry.
Similar results have been found in individuals with clinical diagnoses of anxiety disorders. Adults with panic disorder, for example, showed increased right frontal activity in both resting and anxiety-provoking contexts relative to controls (Wiedemann et al., 1999). Individuals with social phobia also showed increased right frontal activity compared to controls in response to anticipation of giving a speech (Davidson et al., 2000). Additionally, participants with post-traumatic stress disorder showed greater state-dependent right frontal activity when they were presented with trauma-relevant stimuli (Meyer et al., 2015). When participants engaged in an emotional Stroop task consisting of human faces depicting various emotions, those participants with greater levels of trait anxiety showed increased right frontal activity in response to fearful faces than did those with lower levels of trait anxiety (Avram et al., 2010). Similarly, participants who scored higher in trait anxiety showed greater right frontal activity during anxiety-provoking situations (Balconi & Pagani, 2014; Cole et al., 2012; Crost et al., 2008).
242 EDDIE HARMON-JONES, TAYLOR POPP, AND PHILIP A. GABLE
Inconsistent patterns of frontal asymmetry have been found in children with anxiety disorders. In a study comparing resting data of boys and girls aged 8 years and 11 years, anxious girls aged 8 and 11 showed decreased relative left frontal activity at rest, while their healthy control counterparts showed no significant frontal asymmetry at 8 years and greater relative left frontal activity at 11 years. While these results are consistent with research on adults with anxiety disorders, the young boys in the study showed inconsistent patterns. Anxious 8-year-old boys showed no significant frontal asymmetry and anxious 11-year-old boys showed greater relative left frontal activity while healthy boys showed greater relative right frontal activity (Baving et al.,, 2002). These results suggest that patterns of frontal asymmetry in the context of anxiety are not consistent across gender and age; further research is needed to better understand this relationship.
Inconsistent patterns have also been found when comparing various subtypes of anxiety. For instance, at baseline, participants with generalized anxiety disorder and increased worry show greater relative left frontal activity while those with high trait anxiety and low worry show lower relative left frontal activity (Smith et al., 2016). Crost and colleagues (2008) also found that those with more anxiety show greater relative right frontal activity in response to social threat while those higher in defensiveness show greater relative left frontal activity in response to social threat. It has further been argued that symptoms of anxious arousal (e.g., panic) are correlated with lower relative left frontal activity and symptoms of anxious apprehension (e.g., worry) are correlated with greater relative left frontal activity. As these results suggest, symptoms of anxiety have complex relationships with patterns of frontal asymmetry.
#### **11.9.3 Bipolar Disorder**
Individuals with bipolar disorder experience heightened approach motivation and hypersensitivity to goal- and reward-relevant cues during episodes of mania/hypomania (Alloy & Abramson, 2010; Johnson, 2005; Urosevic et al., 2010). This trend is indicative of increased BAS sensitivity in individuals with bipolar disorder. Indeed, self-reported BAS sensitivity scores are higher in those with bipolar I disorder (Meyer et al., 2001; Salavert et al., 2007), bipolar II disorder, and cyclothymia (Alloy et al., 2008), as well as those prone to hypomanic symptomology (Meyer et al., 1999). Since increased BAS sensitivity and approach motivation are positively correlated with relative left frontal cortical activity, it is expected that this trend should be found in individuals with bipolar disorder. Kano and colleagues (1992) collected resting EEG data from participants with bipolar disorder and found greater left frontal cortical activation, suggesting that those experiencing manic symptoms (as opposed to depressive symptoms) have greater relative left frontal activity at baseline.
Nusslock and colleagues (2012) also measured resting EEG frontal asymmetry in individuals with cyclothymia and followed up approximately 5 years later to observe changes in bipolar course. Those with greater levels of left frontal activity at baseline had a greater likelihood of converting to more severe diagnoses over the interim period (i.e., conversion from cyclothymia or bipolar II to bipolar I). Greater relative left
ASYMMETRIC FRONTAL CORTICAL ACTIVITY 243
frontal activity at baseline was also predictive of earlier age-of-onset of a first bipolar spectrum episode, an indicator of severity of bipolar disorder. This relationship was observed even when controlling for mood state and medication status at the time of EEG recording.
An early study by Harmon-Jones and colleagues (2002) also found associations between bipolar disorder and frontal asymmetry in a task-based paradigm. In this study, participants completed the General Behavior Inventory (GBI; Depue et al., 1989) to assess potential risk for developing bipolar or depressive disorders. Then, EEG data was collected while participants engaged in an anger-evoking task. The authors hypothesized that individuals with hypomania/mania symptoms would have greater relative left frontal activity when angered, based on prior research (Depue & Iacono, 1989). They also hypothesized that the opposite pattern (a decrease in left frontal activity) would be seen in participants with depressive symptoms. As predicted, those with hypomanic/ manic symptoms showed increased left frontal activity during the anger-inducing situation while those with depressive symptoms showed decreased left frontal activity. These results suggest that the greater approach tendencies experienced by those with hypomanic/manic symptoms and the diminished approach tendencies experienced by those with depressive symptoms manifest through variations in frontal asymmetry.
Harmon-Jones and colleagues (2008) tested the BAS dysregulation theory of bipolar disorder by measuring frontal asymmetry in response to tasks of varying difficulty. Participants had either a bipolar spectrum diagnosis or no major psychopathology. During EEG data collection, participants engaged in an anagram task during which they were given cues indicating the difficulty (i.e., easy, medium, or hard) of the upcoming trial. They were also told whether they could receive money (win) or avoid losing money (loss) by successfully completing the upcoming trial. Results indicated that those with bipolar disorder had greater relative left frontal activity in preparation for hard/win trials, while control participants showed a decrease in relative left frontal activity in anticipation of the same trial type. Greater relative left frontal activity was also correlated with self-reported hypomanic/manic experience during the task in individuals with bipolar disorder. These results therefore provide evidence supporting BAS dysregulation theory. They also suggest that increased relative left frontal activity, which may be related to manic symptoms, can be triggered by more difficult and rewarding stimuli.
# **11.10 Discussion of Reviewed Research**
## **11.10.1 Non-Significant Associations of Frontal Asymmetry and Affect/Motivation**
Some studies have reported non-significant correlations of resting baseline frontal asymmetry with trait affective valence/motivational direction measures (Reid et al., 244 EDDIE HARMON-JONES, TAYLOR POPP, AND PHILIP A. GABLE
1998). A meta-analysis of the association between affect-related personality traits and frontal asymmetry found that some associations were non-existent, and some were statistically significant in the predicted direction, but with small effect sizes (Kuper et al., 2019). We believe it is important to consider the complexity of human traits and neurophysiology before drawing conclusions about the interpretation of null-effects and small effect sizes of psychological phenomena. Next, we discuss the concerns of interpreting effect sizes and reasons some frontal asymmetry effects may be "small".
As it stands, effect sizes are generally misrepresented and misunderstood by researchers and readers alike. Funder and Ozer (2019) note that, even when effect sizes are reported and, even more rarely, are interpreted, those interpretations are based on fundamentally flawed standards. The two most common means of interpreting effect sizes are via Cohen's standards and squaring the correlation coefficient r. Funder and Ozer (2019) argue that the former of these techniques is nonsensical and is used out of context of any sort of comparison (Cohen agrees that these standards are not ideal; Cohen, 1977, 1988), while the latter is misleading. Squaring the correlation coefficient changes the scale upon which the effect size is measured, making the effect appear less impactful than it may be in reality.
More foundational to the issue of effect sizes is the field's tendency to dismiss small effect sizes without proper consideration. As Funder and Ozer (2019) point out, the reality is that small effect sizes are the most believable. The human experience is complex, and it is ultimately unrealistic to expect that any one phenomenon being studied (neural or behavioral) will explain the bulk of any human behavior. In addition, small effect sizes are not necessarily associated with small consequences. Immediate but frequent phenomena with seemingly small effect sizes can cumulate to have greater implications in the long run of the individual or the population (Funder & Ozer, 2019). "Small" effect sizes should not be dismissed; rather, they should be reported explicitly in the context of their overall consequence. The results of Kuper and colleagues' (2019) meta-analysis also revealed much heterogeneity in results from individual studies, suggesting that situational variables may influence the relationship between resting, baseline frontal asymmetry and self-reported personality traits.
The inconsistency observed in the literature concerning frontal asymmetry could be a result of several things that do not necessarily indicate a lack of relationship with motivation. Motivational tendencies can be sensitive to individual situations, and their relationship to frontal asymmetry could be masked by situational variables. For instance, some research suggests that in baseline EEG recording sessions, half of the variation in the data is due to trait influences and half is due to state influences (Hagemann et al., 2002; Hagemann et al., 2005).
The relationship between trait BAS and resting relative left frontal activity may be influenced by the specific circumstances of an experiment's procedure. Wacker and colleagues (2013) demonstrated this by analyzing the effect of attractiveness of oppositesex experimenter on the correlation between trait BAS and frontal asymmetry. Results suggested that the correlation between BAS and greater relative left frontal activity was present primarily in cases when male participants interacted with attractive female ASYMMETRIC FRONTAL CORTICAL ACTIVITY 245
experimenters. The attractiveness of the experimenter seems to have encouraged approach motivation in the participants, thereby strengthening the relationship between trait BAS and resting relative left frontal activity.
A similar pattern can be seen when reward and effort are manipulated. Hughes and colleagues (2015) conducted an experiment in which low-effort trials elicited low rewards while high-effort trials elicited high rewards. Participants showed greater left frontal activity during high-effort high-reward trials than during low-effort lowrewards trials. These results suggest that the motivation and incentive anticipation involved in a situation can impact measures of frontal asymmetry.
Situational variables outside of the lab space can also impact frontal asymmetry measures. Peterson and Harmon-Jones (2009) found that participants had greater right frontal activity when they participated in the study during fall mornings. Because depression may be experienced more during the fall months (King et al., 2000) and cortisol levels are high in the mornings (King et al., 2000), the variation in frontal asymmetry may have been due to reductions in approach motivation associated with depression and increases in inhibition or withdrawal motivation associated with higher cortisol.
Despite some inconsistencies in the literature, there is sufficient evidence to suggest a relationship between trait motivational tendencies and frontal asymmetry. There are at least three possible explanations for this trend in resting frontal asymmetry data. First, resting frontal asymmetry may reflect neural tendencies of the individual; when they are not engaged in a specific task, their frontal asymmetry scores reflect their trait-based tendencies toward approach and effortful control. Second, resting frontal asymmetry could reflect the individual's response to being in a novel environment. If participants feel curiosity (approach) when introduced to the lab space, they exhibit greater relative left frontal activity; if participants feel discomfort while continuing to engage in the new setting (and engage effortful control), they exhibit greater relative right frontal activity. Third, participants' thought processes during resting data collection could be driving frontal asymmetry variability. When not given any instruction, if participants tend to think about their goals and aspirations, they may exhibit greater relative left frontal activity; if participants tend to think about anxiety evoking situations, they may exhibit greater relative right frontal activity. The underlying mechanisms driving baseline frontal asymmetry are not yet understood and require further research.
## **11.11 CONCLUSION**
The motivational model of frontal asymmetry suggests that relative left frontal activity is associated with approach motivation while right frontal activity is associated with withdrawal motivation. The former assumption of this model is supported by the literature, both through possible motivation confounds associated with the affective valence model and through more direct manipulations of motivation. Anger—an emotion that is both negative and approach motivated—is associated with greater left frontal activity 246 EDDIE HARMON-JONES, TAYLOR POPP, AND PHILIP A. GABLE
at the state and trait level. Further support stems from research connecting higher BAS scores with greater baseline left frontal activity. The connection between BIS scores and baseline right frontal activity, however, has been widely contested.
This inconsistency in the literature concerning withdrawal motivation and right frontal has led to the development of the effortful control model of right frontal asymmetry. The effortful control model suggests that right frontal activity is associated with control and regulatory processing. Research supporting the effortful control model has linked right frontal activity with increased anxious inaction, error detection, and emotional control-related behaviors; right frontal activity is also negatively correlated with state and trait impulsivity. Past work linking right frontal activity and withdrawal motivation may have activated effortful control, because withdrawal manipulations may have co-activated effortful control to stay engaged with the aversive stimuli, but also because activation of r-BIS increases the cognitive load devoted to negative stimuli.
Psychopathologies influence patterns of frontal asymmetry. For instance, individuals with depression show reduced levels of left frontal activity at rest and during emotionally salient tasks. Reduced left frontal activity may be a risk factor for depression in nonclinical populations. Those with anxiety generally show increased levels of right frontal activity at rest and during tasks that elicit fear and/or anxiety; however, this relationship is more complicated in children and when comparing subtypes of anxiety. Those with bipolar disorder who experience manic symptoms exhibit greater left frontal activity at rest and during anger-evoking or difficult rewarding tasks. These patterns are consistent with the motivational direction and effortful control models of frontal asymmetry.
While there have been failures to replicate some past frontal asymmetry findings, these failures to replicate may be due to the complex nature of the systems underlying frontal asymmetry. Phenomena such as affect and motivation change by the moment and can be swayed by situational effects. Despite this, frontal asymmetry research has a long and well-established history in EEG frequency research and continues to spark new predictions, models, and discoveries.
#### **REFERENCES**
- Alema, G., Rosadini, G., & Rossi, G. F. (1961). Preliminary experiments on the effects of the intracarotid introduction of sodium amytal in parkinsonian syndromes. *Bollettino della Società Italiana di Biologia Sperimentale*, *37*, 1036–1037.
- Allen, J. J. B., Harmon-Jones, E., & Cavender, J. H. (2001). Manipulation of frontal EEG asymmetry through biofeedback alters self-reported emotional responses and facial EMG. *Psychophysiology*, *38*, 685–693.
- Allen, J. J. B., Iacono, W. G., Depue, R. A., & Arbisi, P. (1993). Regional electroencephalographic asymmetries in bipolar seasonal affective disorder before and after exposure to bright light. *Biological Psychiatry*, *33*, 642–646.
- Alloy, L. B., Abramson, L. Y., Walshaw, P. D., Cogswell, A., Grandin, L. D., Hughes, M. E., ... & Hogan, M. E. (2008). Behavioral approach system and behavioral inhibition system
ASYMMETRIC FRONTAL CORTICAL ACTIVITY 247
- sensitivities and bipolar spectrum disorders: Prospective prediction of bipolar mood episodes. *Bipolar Disorders*, *10*(2), 310–322.
- Alloy, L. B., & Abramson, L. Y. (2010). The role of the behavioral approach system (BAS) in bipolar spectrum disorders. *Current Directions in Psychological Science*, *19*(3), 189–194.
- Amodio, D. M., Master, S. L. Yee, C. M., & Taylor, S. E. (2008). Neurocognitive components of behavioral inhibition and activation systems: Implications for theories of self-regulation. *Psychophysiology*, *45*, 11–19.
- Amodio, D. M., Shah, J. Y., Sigelman, J., Brazy, P. C., & Harmon-Jones, E. (2004). Implicit regulatory focus associated with resting frontal cortical asymmetry. *Journal of Experimental Social Psychology*, *40*, 225–232.
- Arns, M., Bruder, G., Hegerl, U., Spooner, C., Palmer, D. M., Etkin, A., ... & Gordon, E. (2016). EEG alpha asymmetry as a gender-specific predictor of outcome to acute treatment with different antidepressant medications in the randomized iSPOT-D study. *Clinical Neurophysiology*, *127*(1), 509–519.
- Aron, A. R., Robbins, T. W., & Poldrack, R. A. (2004). Inhibition and the right inferior frontal cortex. *Trends in Cognitive Sciences*, *8*(4), 170–177. doi:10.1016/j.tics.2004.02.010
- Aron, A. R., Robbins, T. W., & Poldrack, R. A. (2014). Inhibition and the right inferior frontal cortex: One decade on. *Trends in Cognitive Sciences*, *18*(4), 177–185. doi:10.1016/ j.tics.2013.12.003
- Avram, J., Balteş, F. R., Miclea, M., & Miu, A. C. (2010). Frontal EEG activation asymmetry reflects cognitive biases in anxiety: Evidence from an emotional face Stroop task. *Applied Psychophysiology and Biofeedback*, *35*(4), 285–292. doi:10.1007/ s10484–010-9138–6
- Balconi, M. & Pagani, S. (2014). Personality correlates (BAS-BIS), self-perception of social ranking, and cortical (alpha frequency band) modulation in peer-group comparison. *Physiology & Behavior*, *133*, 207–215. doi:10.1016/j.physbeh.2014.05.043
- Bari, A. & Robbins, T. W. (2013). Inhibition and impulsivity: Behavioral and neural basis of response control. *Progress in Neurobiology*, *108*, 44–79. doi:10.1016/j.pneurobio.2013.06.005
- Baving, L., Laucht, M., & Schmidt, M. H. (2002). Frontal brain activation in anxious school children. *Journal of Child Psychology and Psychiatry, and Allied Disciplines*, *43*(2), 265–274.
- Beeney, J. E., Levy, K. N., Gatzke-Kopp, L. M., & Hallquist, M. N. (2014). EEG asymmetry in borderline personality disorder and depression following rejection. *Personality Disorders: Theory, Research, and Treatment*, *5*, 178–185.
- Berkman, E. T. & Lieberman, M. D. (2010). Approaching the bad and avoiding the good: Lateral prefrontal cortical asymmetry distinguishes between action and valence. *Journal of Cognitive Neuroscience*, *22*(9), 1970–1979. doi:10.1162/jocn.2009.21317
- Berkowitz, L. & Harmon-Jones, E. (2004). Toward an understanding of the determinants of anger. *Emotion*, *4*, 107–130.
- Bickel, W. K., Jarmolowicz, D. P., Mueller, E. T., Gatchalian, K. M., & McClure, S. M. (2012). Are executive function and impulsivity antipodes? A conceptual reconstruction with special reference to addiction. *Psychopharmacology*, *221*(3), 361–387. doi:10.1007/ s00213–012-2689-x
- Black, E W. (1975). Unilateral brain lesions and MMPI performance: A preliminary study. *Perceptual and Motor Skills*, *40*, 87–93.
- Blanchard R. J. & Blanchard D. C. (1984). Affect and aggression: An animal model applied to human behavior. In R. J. Blanchard, & D. C. Blanchard (Eds.), *Advances in the study of aggression* (pp. 1–62). Academic Press.
- Brehm, J. W. (1999). The intensity of emotion. *Personality and Social Psychology Review*, *3*, 2–22.
248 EDDIE HARMON-JONES, TAYLOR POPP, AND PHILIP A. GABLE
- Brehm, J. W., & Self, E. A. (1989). The intensity of motivation. *Annual Review of Psychology*, *40*, 109–131.
- Bruder, G. E., Stewart, J. W., Tenke, C. E., McGrath, P. J., Leite, P., Bhattacharya, N., & Quitkin, F. M. (2001). Electroencephalographic and perceptual asymmetry differences between responders and nonresponders to an SSRI antidepressant. *Biological psychiatry*, *49*(5), 416–425.
- Carter, B. L. & Tiffany, S. T. (1999). Meta-analysis of cue-reactivity in addiction research. *Addiction*, *94*(3), 327–340. doi:10.1046/ j.1360-0443.1999.9433273.x
- Carver, C. S. (2004). Negative affects deriving from the behavioral approach system. *Emotion*, *4*, 3–22.
- Carver, C. S. & Connor-Smith, J. (2010). Personality and coping. *Annual Review of Psychology*, *61*, 679–704. doi:10.1146/annurev.psych.093008.100352
- Carver, C. S. & Harmon-Jones, E. (2009). Anger is an approach-related affect: Evidence and implications. *Psychological Bulletin*, *135*, 183–204.
- Carver, C. S. & White, T. L. (1994). Behavioral inhibition, behavioral activation, and affective responses to impending reward and punishment: The BIS/BAS scales. *Journal of Personality and Social Psychology*, *67*, 319–333.
- Carver, C. S., Johnson, S. L., & Joormann, J. (2008). Serotonergic function, two-mode models of self-regulation, and vulnerability to depression: What depression has in common with impulsive aggression. *Psychological bulletin*, *134*(6), 912. doi:10.1037/ a0013740
- Coan, J. A. & Allen, J. J. (2003). Frontal EEG asymmetry and the behavioral activation and inhibition systems. *Psychophysiology*, *40*, 106–114.
- Coan, J. A. & Allen, J. J. (2004). Frontal EEG asymmetry as a moderator and mediator of emotion. *Biological Psychology*, *67*, 7–50.
- Coan, J. A., Allen, J. J. B., & Harmon-Jones, E. (2001). Voluntary facial expression and hemispheric asymmetry over the frontal cortex. *Psychophysiology*, *38*, 912–925.
- Cohen, J. (1977). *Statistical power analysis for the behavioral sciences* (rev. ed.). Academic Press. Cohen, J. (1988). *Statistical power analysis for the behavioral sciences* (2nd ed.). Erlbaum.
- Cole, C., Zapp, D. J., Nelson, S. K., & Perez-Edgar, K. (2012). Speech presentation cues moderate frontal EEG asymmetry in socially withdrawn young adults. *Brain and Cognition*, *78*(2), 156–162. doi:10.1016/j.bandc.2011.10.013
- Cook, I. A., O'Hara, R., Uijtdehaage, S. H. J., Mandelkern, M., & Leuchter, A. F. (1998). Assessing the accuracy of topographic EEG mapping for determining local brain function. *Electroencephalography and Clinical Neurophysiology*, *107*, 408–414.
- Crost, N. W., Pauls, C. A., & Wacker, J. (2008). Defensiveness and anxiety predict frontal EEG asymmetry only in specific situational contexts. *Biological Psychology*, *78*(1), 43–52. doi:10.1016/j. biopsycho.2007.12.008
- Cyders, M. A., & Smith, G. T. (2007). Mood-based rash action and its components: Positive and negative urgency. *Personality and Individual Differences*, *43*(4), 839–850. doi:10.1016/ j.paid.2007. 02.008
- Cyders, M. A., Zapolski, T. C., Combs, J. L., Settles, R. F., Fillmore, M. T., & Smith, G. T. (2010). Experimental effect of positive urgency on negative outcomes from risk taking and on increased alcohol consumption. *Psychology of Addictive Behaviors*, *24*(3), 367–375.
- Darwin, C. (1872/1965). *The expressions of the emotions in man and animals*. Oxford University Press.
- Davidson, R. J. & Fox, N. (1982). Asymmetric brain activity discriminates between positive and negative affective stimuli in 10 month old infants. *Science*, *218*, 1235–1237.
ASYMMETRIC FRONTAL CORTICAL ACTIVITY 249
- Davidson, R. J., Chapman, J. P., Chapman, L. J., & Henriques, J. B. (1990). Asymmetric brain electrical-activity discriminates between psychometrically-matched verbal and spatial cognitive tasks. *Psychophysiology*, *27*, 528–543.
- Davidson, R. J., Marshall, J. R., Tomarken, A. J., & Henriques, J. B. (2000). While a phobic waits: Regional brain electrical and autonomic activity in social phobics during anticipation of public speaking. *Biological Psychiatry*, *47*(2), 85–95. [https://doi.org/10.1016/](https://doi.org/10.1016/s0006-3223(99)00222-x) [s0006-3223\(99\)00222-x](https://doi.org/10.1016/s0006-3223(99)00222-x)
- Davidson, R. J., Pizzagalli, D., Nitschke, J. B., & Putnam, K. (2002). Depression: Perspectives from affective neuroscience. *Annual Review of Psychology*, *53*, 545–574. [doi:10.1146/annurev.](http://doi:10.1146/annurev.psych.53.100901.135148%22) [psych.53.100901.135148](http://doi:10.1146/annurev.psych.53.100901.135148%22)
- De Pascalis, V., Cozzuto, G., Caprara, G. V., & Alessandri, G. (2013). Relations among EEGalpha asymmetry, BIS/BAS, and dispositional optimism. *Biological Psychology*, *94*, 198–209.
- Depue, R. A., Krauss, S., Spoont, M. R., & Arbisi, P. (1989). General Behavior Inventory identification of unipolar and bipolar affective conditions in a nonclinical university population. *Journal of Abnormal Psychology*, *98*(2), 117–126.
- Depue, R.A. & Iacono, W.G. (1989). Neurobehavioral aspects of affective disorders. *Annual Review of Psychology*, *40*, 457–492.
- Derryberry, D. & Rothbart, M. K. (1997). Reactive and effortful processes in the organization of temperament. *Development and Psychopathology*, *9*(4), 633–652. doi:10.1017/ S095457949700 1375
- DeYoung, C. G. (2015). Cybernetic big five theory. *Journal of Research in Personality*, *56*, 33–58. doi:10.1016/j.jrp.2014.07.004
- Diego, M. A., Field, T., & Hernandez-Reif, M. (2001). CES-D depression scores are correlated with frontal EEG alpha asymmetry. *Depression and Anxiety*, *13*(1), 32–37.
- Eisenberg, N., Spinrad, T. L., Fabes, R. A., Reiser, M., Cumberland, A., Shepard, S. A., ... Thompson, M. (2004). The relations of effortful control and impulsivity to children's resiliency and adjustment. *Child Development*, *75*(1), 25–46. doi:10.1111/j.1467- 8624.2004.00652.x
- Ekman, P. & Davidson, R. J. (1993). Voluntary smiling changes regional brain activity. *Psychological Science*, *4*, 342–345.
- Ekman, P. & Friesen, W. V. (1975). *Unmasking the face: A guide to recognizing emotions from facial clues*. Prentice-Hall.
- Elgavish, E., Halpern, D., Dikman, Z., & Allen, J. J. B. (2003). Does frontal EEG asymmetry moderate or mediate responses to the international affective picture system (IAPS)? *Psychophysiology*, *40*, S38.
- Enticott, P. G., Ogloff, J. R., & Bradshaw, J. L. (2006). Associations between laboratory measures of executive inhibitory control and self-reported impulsivity. *Personality and Individual Differences*, *41*(2), 285–294. doi:10.1016/j.paid.2006.01.011
- Feldmann, L., Piechaczek, C. E., Grünewald, B. D., Pehl, V., Bartling, J., Frey, M., ... & Greimel, E. (2018). Resting frontal EEG asymmetry in adolescents with major depression: impact of disease state and comorbid anxiety disorder. *Clinical Neurophysiology*, *129*(12), 2577–2585.
- Funder, D. C. & Ozer, D. J. (2019). Evaluating effect size in psychological research: Sense and nonsense. *Advances in Methods and Practices in Psychological Science*, *2*(2), 156–168.
- Gable, P. A. & Dreisbach, G. (2021). Approach motivation and positive affect. *Current Opinion in Behavioral Sciences*, *39*, 203–208.
- Gable, P. A. & Harmon-Jones, E. (2008). Relative left frontal activation to appetitive stimuli: Considering the role of individual differences. *Psychophysiology*, *45*, 275–278.
250 EDDIE HARMON-JONES, TAYLOR POPP, AND PHILIP A. GABLE
- Gable, P. A. & Poole, B. D. (2014). Influence of trait behavioral inhibition and behavioral approach motivation systems on the LPP and frontal asymmetry to anger pictures. *Social Cognitive and Affective Neuroscience*, *9*, 182–190.
- Gable, P. A., Mechin, N. C., Hicks, J. A., & Adams, D. L. (2015). Supervisory control system and frontal asymmetry: Neurophysiological traits of emotion-based impulsivity. *Social, Cognitive, and Affective Neuroscience*, *10*(10), 1310–315.
- Gable, P. A., Mechin, N., Hicks, J.A., & Adams, D.A. (2015). Positive urgency and left-frontal asymmetry: Neurophysiological traits of emotion-based impulsivity. *Social Cognitive and Affective Neuroscience*, *10*, 1310–1315
- Gable, P. A., Neal, L. B., & Threadgill, A. H. (2018). Regulatory behavior and frontal activity: Considering the role of revised-BIS in relative right frontal asymmetry. *Psychophysiology*, *55*(1), e12910.
- Gable, P. A., Poole, B. D., & Cook, M. S. (2013). Asymmetrical hemisphere activation enhances global-local processing. *Brain and Cognition*, *83*, 337–341.
- Gainotti, G. (1972). Emotional behavior and hemispheric side of the lesion. *Cortex*, *8*, 41–55.
- Gasparrini, W. G., Satz, P., Heilman, K., & Coolidge, F. L. (1978). Hemispheric asymmetries of affective processing as determined by the Minnesota Multiphasic Personality Inventory. *Journal of Neurology, Neurosurgery and Psychiatry*, *41*, 470–473.
- Gianotti, L. R., Knoch, D., Faber, P. L., Lehmann, D., Pascual-Marqui, R. D., Diezi, C., ... & Fehr, E. (2009). Tonic activity level in the right prefrontal cortex predicts individuals' risk taking. *Psychological Science*, *20*, 33–38.
- Goldstein, K. (1939). *The organism: An holistic approach to biology, derived from pathological data in man*. American Books.
- Gray, J. (1982). Précis of *The neuropsychology of anxiety*: *An enquiry into the functions of the septo-hippocampal system*. *Behavioral and Brain Sciences*, *5*(3), 469–484. doi:10.1017/ S0140525X00013066
- Gray, J. A. & McNaughton, N. (2000). *The neuropsychology of anxiety: An enquiry into the functions of the septo-hippocampal system* (2nd ed.). Oxford University Press.
- Grimshaw, G. M. & Carmel, D. (2014). An asymmetric inhibition model of hemispheric differences in emotional processing. *Frontiers in Psychology*, *5*, 489. [doi:10.3389/](http://doi:10.3389/fpsyg.2014.00489%22) [fpsyg.2014.00489](http://doi:10.3389/fpsyg.2014.00489%22)
- Gross, J. J. & Levenson, R. W. (1993). Emotional suppression: Physiology, self-report, and expressive behavior. *Journal of Personality and Social Psychology*, *64*, 970–986. doi:10.1037/ 0022- 3514.64.6.970
- Hagemann, D., Hewig, J., Seifert, J., Naumann, E., & Bartussek, D. (2005). The latent statetrait structure of resting EEG asymmetry: Replication and extension. *Psychophysiology*, *42*, 740–752.
- Hagemann, D., Naumann, E., Becker, G., Maier, S., & Bartussek, D. (1998). Frontal brain asymmetry and affective style: A conceptual replication. *Psychophysiology*, *35*, 372–388.
- Hagemann, D., Naumann, E., Thayer, J. F., & Bartussek, D. (2002). Does resting EEG asymmetry reflect a trait? An application of latent state-trait theory. *Journal of Personality and Social Psychology*, *82*, 619–641.
- Harmon-Jones, C., Schmeichel, B. J., Mennitt, E., & Harmon-Jones, E. (2011). The expression of determination: Similarities between anger and approach-related positive affect. *Journal of Personality and Social Psychology*, *100*, 172–181. doi:10.1037/a0020966
- Harmon-Jones, E. (2003a). Clarifying the emotive functions of asymmetrical frontal cortical activity. *Psychophysiology*, *40*, 838–848.
ASYMMETRIC FRONTAL CORTICAL ACTIVITY 251
- Harmon-Jones, E. (2003b). Anger and the behavioural approach system. *Personality and Individual Differences*, *35*, 995–1005.
- Harmon-Jones, E. (2004). On the relationship of anterior brain activity and anger: Examining the role of attitude toward anger. *Cognition and Emotion*, *18*, 337–361.
- Harmon-Jones, E. (2006). Unilateral right-hand contractions cause contralateral alpha power suppression and approach motivational affective experience. *Psychophysiology*, *43*, 598–603.
- Harmon-Jones, E. (2007). Trait anger predicts relative left frontal cortical activation to angerinducing stimuli. *International Journal of Psychophysiology*, *66*, 154–160.
- Harmon-Jones, E., Abramson, L. Y., Nusslock, R., Sigelman, J. D., Urosevic, S., Turonie, L. D., Alloy, L. B., & Fearn, M. (2008). Effect of bipolar disorder on left frontal cortical responses to goals differing in valence and task difficulty. *Biological Psychiatry*, *63*, 693–698.
- Harmon-Jones, E., Abramson, L. Y., Sigelman, J., Bohlig, A., Hogan, M. E., & Harmon-Jones, C. (2002). Proneness to hypomania/mania or depression and asymmetric frontal cortical responses to an anger-evoking event. *Journal of Personality and Social Psychology*, *82*, 610–618.
- Harmon-Jones, E. & Allen, J. J. B. (1997). Behavioral activation sensitivity and resting frontal EEG asymmetry: Covariation of putative indicators related to risk for mood disorders. *Journal of Abnormal Psychology*, *106*, 159–163.
- Harmon-Jones, E. & Allen, J. J. B. (1998). Anger and prefrontal brain activity: EEG asymmetry consistent with approach motivation despite negative affective valence. *Journal of Personality and Social Psychology*, *74*, 1310–1316.
- Harmon-Jones, E. & Gable, P. A. (2009). Neural activity underlying the effect of approachmotivated positive affect on narrowed attention. *Psychological Science*, *20*, 406–409.
- Harmon-Jones, E. & Gable, P. A. (2018). On the role of asymmetric frontal cortical activity in approach and withdrawal motivation: An updated review of the evidence. *Psychophysiology*, *55*(1), e12879.
- Harmon-Jones, E., Gable, P. A., & Price, T. F. (2011). Leaning embodies desire: Evidence that leaning forward increases relative left frontal activation to appetitive stimuli. *Biological Psychology*, *87*, 311–313.
- Harmon-Jones, E., Harmon-Jones, C., Abramson, L. Y., & Peterson, C. K. (2009). PANAS positive activation is associated with anger. *Emotion*, *9*, 183–196.
- Harmon-Jones, E., Harmon-Jones, C., Amodio, D. M., & Gable, P. A. (2011). Attitudes toward emotions. *Journal of Personality and Social Psychology*, *101*, 1332–1350. doi:10.1037/a0024951
- Harmon-Jones, E., Harmon-Jones, C., Fearn, M., Sigelman, J. D., & Johnson, P. (2008). Left frontal cortical activation and spreading of alternatives: Tests of the action-based model of dissonance. *Journal of Personality and Social Psychology*, *94*, 1–15. doi:10.1037/ 0022-3514.94.1.1
- Harmon-Jones, E., Harmon-Jones, C., & Price, T. F. (2013). What is approach motivation? *Emotion Review*, *5*, 291–295. doi:10.1177/1754073913477509
- Harmon-Jones, E., Lueck, L., Fearn, M., & Harmon-Jones, C. (2006). The effect of personal relevance and approach-related action expectation on relative left frontal cortical activity. *Psychological Science*, *17*, 434–440.
- Harmon-Jones, E. & Peterson, C. K. (2008). Effect of trait and state approach motivation on aggressive inclinations. *Journal of Research in Personality*, *42*, 1381–1385.
- Harmon-Jones, E. & Peterson, C. K. (2009). Supine body position reduces neural response to anger evocation. *Psychological Science*, *20*, 1209–1210. doi:10.1111/j.1467-9280.2009.02416.x
252 EDDIE HARMON-JONES, TAYLOR POPP, AND PHILIP A. GABLE
- Harmon-Jones, E., Peterson, C. K., & Harris, C. R. (2009). Jealousy: Novel methods and neural correlates. *Emotion*, *9*, 113–117.
- Harmon-Jones, E. & Sigelman, J. D. (2001). State anger and prefrontal brain activity: Evidence that insult-related relative left-prefrontal activation is associated with experienced anger and aggression. *Journal of Personality and Social Psychology*, *80*, 797–803.
- Harmon-Jones, E., Sigelman, J. D., Bohlig, A., & Harmon-Jones, C. (2003). Anger, coping, and frontal cortical activity: The effect of coping potential on anger-induced left frontal activity. *Cognition and Emotion*, *17*, 1–24.
- Harmon-Jones, E., Vaughn-Scott, K., Mohr, S., Sigelman, J., & Harmon-Jones, C. (2004). The effect of manipulated sympathy and anger on left and right frontal cortical activity. *Emotion*, *4*, 95–101.
- Hellige, J. B. (1993). *Hemispheric asymmetry: What's right and what's left*. Harvard University Press.
- Henriques, J. B. & Davidson, R. J. (1990). Regional brain electrical asymmetries discriminate between previously depressed and healthy control subjects. *Journal of Abnormal Psychology*, *99*, 22–31.
- Henriques, J. B. & Davidson, R. J. (2000). Decreased responsiveness to reward in depression. *Cognition & Emotion*, *14*(5), 711–724. doi:10.1080/02699930050117684
- Hester, R. & Garavan, H. (2004). Executive dysfunction in cocaine addiction: Evidence for discordant frontal, cingulate, and cerebellar activity. *The Journal of Neuroscience*, *24*(49), 11017– 11022. doi:10.1523/JNEUROSCI.3321-04.2004
- Hester, R. & Garavan, H. (2009). Neural mechanisms underlying drug-related cue distraction in active cocaine users. *Pharmacology Biochemistry and Behavior*, *93*(3), 270–277. doi:10.1016/j. pbb.2008.12.009
- Hewig, J., Hagemann, D., Seifert, J., Naumann, E., & Bartussek, D. (2004). On the selective relation of frontal cortical activity and anger-out versus anger-control. *Journal of Personality and Social Psychology*, *87*, 926–939.
- Hewig, J., Hagemann, D., Seifert, J., Naumann, E., & Bartussek, D. (2006). The relation of cortical activity and BIS/BAS on the trait level. *Biological Psychology*, *71*(1), 42–53. doi:10.1016/j. biopsycho.2005.01.006
- Heym, N., Ferguson, E., & Lawrence, C. (2008). An evaluation of the relationship between Gray's revised RST and Eysenck's PEN: Distinguishing BIS and FFFS in Carver and White's BIS/BAS scales. *Personality and Individual Differences*, *45*(8), 709–715. doi:10.1016/ j.paid.2008.07.013
- Hughes, D. M., Yates, M. J., Morton, E. E., & Smillie, L. D. (2015). Asymmetric frontal cortical activity predicts effort expenditure for reward. *Social Cognitive and Affective Neuroscience*, *10*, 1015–1019.
- Jackson, D. C., Mueller, C. J., Dolski, I., Dalton, K. M., Nitschke, J. B., Urry, H. L., ... & Davidson, R. J. (2003). Now you feel it, now you don't: Frontal brain electrical asymmetry and individual differences in emotion regulation. *Psychological Science*, *14*(6), 612–617. doi:10.1046/ j.0956-7976.2003.psci\_1473.x
- Jacobs, G. D. & Snyder, D. (1996). Frontal brain asymmetry predicts affective style in men. *Behavioral Neuroscience*, *110*, 3–6.
- Jensen-Campbell, L. A., Knack, J. M., Waldrip, A. M., & Campbell, S. D. (2007). Do big five personality traits associated with self-control influence the regulation of anger and aggression? *Journal of Research in Personality*, *41*, 403–424.
ASYMMETRIC FRONTAL CORTICAL ACTIVITY 253
- Johnson, S. L. (2005). Mania and dysregulation in goal pursuit: A review. *Clinical Psychology Review*, *25*, 241–262.
- Kamiya, J. (1979). Autoregulation of the EEG alpha rhythm: A program for the study of consciousness. In S. A. E. Peper & M. Quinn (Eds.), *Mind/body integration: Essential readings in biofeedback* (pp. 289–297). Plenum Press.
- Kano, K., Nakamura, M., Matsuoka, T., Iida, H., & Nakajima, T. (1992). The topographical features of EEGs in patients with affective disorders. *Electroencephalography and Clinical Neurophysiology*, *83*, 124–129.
- Keune, P. M., Bostanov, V., Kotchoubey, B., & Hautzinger, M. (2012). Mindfulness versus rumination and behavioral inhibition: A perspective from research on frontal brain asymmetry. *Personality and Individual Differences*, *53*(3), 323–328. doi:10.1016/j. paid.2012.03.034
- Keune, P. M., Schönenberg, M., Wyckoff, S., Mayer, K., Riemann, S., Hautzinger, M., & Strehl, U. (2011). Frontal alpha-asymmetry in adults with attention deficit hyperactivity disorder: Replication and specification. *Biological Psychology*, *87*, 306–310.
- Keune, P. M., van der Heiden, L., Várkuti, B., Konicar, L., Veit, R., & Birbaumer, N. (2012). Prefrontal brain asymmetry and aggression in imprisoned violent offenders. *Neuroscience Letters*, *515*, 191–195.
- King, J. A., Rosal, M. C., Ma, Y., Reed, G., Kelly, T., Stanek, III, E.J., & Ockene, I. S. (2000). Sequence and seasonal effects of salivary cortisol. *Behavioral Medicine*, *26*, 67–73.
- Kline, J. P., Blackhart, G. C., Woodward, K. M., Williams, S. R., & Schwartz, G. E. (2000). Anterior electroencephalographic asymmetry changes in elderly women in response to a pleasant and an unpleasant odor. *Biological Psychology*, *52*(3), 241–250. doi:10.1016/ S0301-0511(99)00046-0
- Knoch, D., Gianotti, L. R., Baumgartner, T., & Fehr, E. (2010). A neural marker of costly punishment behavior. *Psychological Science*, *21*(3), 337–342. doi:10.1177/0956797609360750
- Kochanska, G. & Knaack, A. (2003). Effortful control as a personality characteristic of young children: Antecedents, correlates, and consequences. *Journal of Personality*, *71*(6), 1087–1112. doi:10.1111/1467-6494.7106008
- Kuper, N., Käckenmester, W., & Wacker, J. (2019). Resting frontal EEG asymmetry and personality traits: A meta-analysis. *European Journal of Personality*, *33*(2), 154–175.
- Lacey, M. F., Neal, L. B., & Gable, P. A. (2020). Effortful control of motivation, not withdrawal motivation, relates to greater right frontal asymmetry. *International Journal of Psychophysiology*, *147*, 18–25.
- Lagerspetz, K. M. J. (1969). Aggression and aggressiveness in laboratory mice. In S. Garattini, & E. B. Sigg (Eds.), *Aggressive Behavior* (pp. 77–85). Wiley.
- Lazarus, R. S. (1991). *Emotion and adaptation*. Oxford University Press.
- Logan, G. D., Schachar, R. J., & Tannock, R. (1997). Impulsivity and inhibitory control. *Psychological Science*, *8*(1), 60–64. doi:10.1111/j.1467-9280.1997.tb00545.x
- Mathersul, D., Williams, L. M., Hopkinson, P. J., & Kemp, A. H. (2008). Investigating models of affect: Relationships among EEG alpha asymmetry, depression, and anxiety. *Emotion*, *8*(4), 560–572
- McFarland, B. R., Shankman, S. A., Tenke, C. E., Bruder, G. E., & Klein, D. N. (2006). Behavioral activation system deficits predict the six-month course of depression. *Journal of Affective Disorders*, *91*(2–3), 229–234.
- Mechin, N., Gable, P. A., & Hicks, J. A. (2016). Frontal asymmetry and alcohol cue reactivity: Influence of core personality systems. *Psychophysiology*, *53*(8), 1224–1231. doi:10.1111/ psyp.12659
254 EDDIE HARMON-JONES, TAYLOR POPP, AND PHILIP A. GABLE
- Metzger, L. J., Paige, S. R., Carson, M. A., Lasko, N. B., Paulus, L. A., Pitman, R. K., & Orr, S. P. (2004). PTSD arousal and depression symptoms associated with increased right-sided parietal EEG asymmetry. *Journal of Abnormal Psychology*, *113*(2), 324–329.
- Meyer, B., Johnson, S. L., & Carver, C. S. (1999). Exploring behavioral activation and inhibition sensitivities among college students at risk for bipolar spectrum symptomatology. *Journal of Psychopathology and Behavioral Assessment*, *21*, 275–292.
- Meyer, B., Johnson, S.L., & Winters, R. (2001). Responsiveness to threat and incentive in bipolar disorder: Relations of the BIS/BAS scales with symptoms. *Journal of Psychopathology and Behavioral Assessment*, *23*, 133–143.
- Meyer, T., Smeets, T., Giesbrecht, T., Quaedflieg, C. W., Smulders, F. T., Meijer, E. H., & Merckelbach, H. L. (2015). The role of frontal EEG asymmetry in post-traumatic stress disorder. *Biological Psychology*, *108*, 62–77. [doi:10.1016/j.biopsycho.2015.03.018](http://doi:10.1016/j.biopsycho.2015.03.018%22)
- Mitchell, A. M. & Pössel, P. (2012). Frontal brain activity pattern predicts depression in adolescent boys. *Biological Psychology*, *89*(2), 525–527.
- Mize, K. D. & Jones, N. A. (2012). Infant physiological and behavioral responses to loss of maternal attention to a social-rival. *International Journal of Psychophysiology*, *83*(1), 16–23. doi:10.1016/j.ijpsycho.2011.09.018
- Murphy, F. C., Nimmo-Smith, I., & Lawrence, A. D. (2003). Functional neuroanatomy of emotion: A meta-analysis. *Cognitive, Affective, & Behavioral Neuroscience*, *3*, 207–233.
- Myrick, H., Anton, R. F., Li, X., Henderson, S., Drobes, D., Voronin, K., & George, M. S. (2004). Differential brain activity in alcoholics and social drinkers to alcohol cues: Relationship to craving. *Neuropsychopharmacology*, *29*(2), 393–402. doi:10.1038/sj.npp.1300295
- Nash, K., Inzlicht, M., & McGregor, I. (2012). Approach-related left prefrontal EEG asymmetry predicts muted error-related negativity. *Biological Psychology*, *91*, 96–102.
- Neal, L. B. & Gable, P. A. (2016). Neurophysiological markers of multiple facets of impulsivity. *Biological Psychology*, *115*, 64–68. doi:10.1016/j.biopsycho.2012.05.005
- Neal, L. B. & Gable, P. A. (2019). Shifts in frontal asymmetry underlying impulsive and controlled decision-making. *Biological Psychology*, *140*, 28–34.
- Nigg, J. T. (2006). Temperament and developmental psychopathology. *Journal of Child Psychology and Psychiatry*, *47*(3-4), 395–422. doi:10.1111/j.1469-7610.2006.01612.x
- Nitschke, J. B., Heller, W., Etienne, M. A., & Miller, G. A. (2004). Prefrontal cortex activity differentiates processes affecting memory in depression. *Biological Psychology*, *67*(1–2), 125–143.
- Nusslock, R., Harmon-Jones, E., Alloy, L. B., Urosevic, S., Goldstein, K., & Abramson, L. Y. (2012). Elevated left mid-frontal cortical activity prospectively predicts conversion to bipolar *I disorder. Journal of Abnormal Psychology*, *121*(3), 592–601. doi:10.1037/a0028973
- Nusslock, R., Shackman, A. J., Harmon-Jones, E., Alloy, L. B., Coan, J. A., & Abramson, L. Y. (2011). Cognitive vulnerability and frontal brain asymmetry: Common predictors of first prospective depressive episode. *Journal of Abnormal Psychology*, *120*, 497–503.
- Nusslock, R., Shackman, A. J., McMenamin, B. W., Greischar, L. L., Davidson, R. J., & Kovacs, M. (2018). Comorbid anxiety moderates the relationship between depression history and prefrontal EEG asymmetry. *Psychophysiology*, *55*(1), e12953.
- Pascual-Marqui, R. D. (2002). Standardized low-resolution brain electromagnetic tomography (sLORETA): Technical details. *Methods and Findings in Experimental and Clinical Pharmacology*, *24* (Suppl D), 5–12.
- Perria, P., Rosadini, G., & Rossi, G. F. (1961). Determination of side of cerebral dominance with Amobarbital. *Archives of Neurology*, *4*, 175–181.
ASYMMETRIC FRONTAL CORTICAL ACTIVITY 255
- Peterson, C. K. & Harmon-Jones, E. (2009). Circadian and seasonal variability of resting frontal EEG asymmetry. *Biological Psychology*, *80*, 315–320.
- Peterson, C. K., Gravens, L., & Harmon-Jones, E. (2011). Asymmetric frontal cortical activity and negative affective responses to ostracism. *Social Cognitive Affective Neuroscience*, *6*, 277– 285. doi:10.1093/scan/nsq027
- Peterson, C. K., Shackman, A. J., & Harmon-Jones, E. (2008). The role of asymmetric frontal cortical activity in aggression. *Psychophysiology*, *45*, 86–92.
- Pizzagalli, D. A., Sherwood, R. J., Henriques, J. B., & Davidson, R. J. (2005). Frontal brain asymmetry and reward responsiveness: A source-localization study. *Psychological Science*, *16*(10), 805–813. doi:10.1111/j.1467-9280.2005.01618.x
- Pizzagalli, D., Shackman, A. J., & Davidson, R. J. (2003). The functional neuroimaging of human emotion: Asymmetric contributions of cortical and subcortical circuitry. In K. Hugdahl & R. J. Davidson (Eds.), *The asymmetric brain* (pp. 511–532). MIT Press.
- Plutchik, R. (1980). *Emotion: A psychoevolutionary synthesis*. HarperCollins College Division.
- Pössel, P., Lo, H., Fritz, A., & Seemann, S. (2008). A longitudinal study of cortical EEG activity in adolescents. *Biological Psychology*, *78*(2), 173–178. [https://doi.org/https://doi.org/10.1016/](https://doi.org/https://doi.org/10.1016/j.biopsycho.2008.02.004) [j.biopsycho.2008.02.004](https://doi.org/https://doi.org/10.1016/j.biopsycho.2008.02.004)
- Price, T. F. & Harmon-Jones, E. (2011). Approach motivational body postures lean toward left frontal brain activity. *Psychophysiology*, *48*, 718–722.
- Price, T. F., Hortensius, R., & Harmon-Jones, E. (2013). Neural and behavioral associations of manipulated determination facial expressions. *Biological Psychology*, *94*, 221–227. [http://](http://dx.doi.org/10.1016/j.biopsycho.2013.06.001) [dx.doi.org/10.1016/j.biopsycho.2013.06.001](http://dx.doi.org/10.1016/j.biopsycho.2013.06.001)
- Proudfit, G. H., Inzlicht, M., & Mennin, D. S. (2013). Anxiety and error monitoring: The importance of motivation and emotion. *Frontiers in Human Neuroscience*, *7*, 636. [doi:10.3389/](http://doi:10.3389/%20fnhum.2013.00636%22) [fnhum.2013.00636](http://doi:10.3389/%20fnhum.2013.00636%22)
- Putman, P., Hermans, E., & van Honk, J. (2004). Emotional Stroop performance for masked angry faces: It's BAS, not BIS. *Emotion*, *4*, 305–311.
- Quaedflieg, C. W. E. M., Smulders, F. T. Y., Meyer, T., Peeters, F. P. M. L., Merckelbach, H. L. G. J., & Smeets, T. (2016). The validity of individual frontal alpha asymmetry EEG neurofeedback. *Social Cognitive and Affective Neuroscience*, *11*, 33–43. Doi: 10.1093/scan/nsv090
- Quirin, M., Gruber, T., Kuhl, J., & Düsing, R. (2013). Is love right? Prefrontal resting brain asymmetry is related to the affiliation motive. *Frontiers in Human Neuroscience*, *7*, 902. doi:10.3389/ fnhum.2013.00902
- Reid, S. A., Duke, L. M., & Allen, J. J. B. (1998). Resting frontal electroencephalographic asymmetry in depression: Inconsistencies suggest the need to identify mediating factors. *Psychophysiology*, *35*, 389–404.
- Robinson, R. G. & Price, T. R. (1982). Post-stroke depressive disorders: A follow-up study of 103 patients. *Stroke*, *13*, 635–641.
- Rodrigues, J., Müller, M., Mühlberger, A., & Hewig, J. (2018). Mind the movement: Frontal asymmetry stands for behavioral motivation, bilateral frontal activation for behavior. *Psychophysiology*, *55*(1), e12908.
- Rossi, G. F. & Rosadini, G. R. (1967). Experimental analyses of cerebral dominance in man. In D. H. Millikan & F. L. Darley (Eds.), *Brain mechanisms underlying speech and language* (pp. 167–184). Grune & Stratton.
- Rothbart, M. K. & Rueda, M. R. (2005). The development of effortful control. In U. Mayr, E. Awh, & S. W. Keele (Eds.), *Developing individuality in the human brain: A tribute to Michael I. Posner* (pp. 167–188). American Psychological Association.
256 EDDIE HARMON-JONES, TAYLOR POPP, AND PHILIP A. GABLE
- Rothbart, M. K., Ellis, L. K., & Posner, M. I. (2004). Temperament and self-regulation. In K. D. Vohs & R. F. Baumeister (Eds.), *Handbook of self-regulation: Research, theory, and applications* (pp. 284–299). Guilford Press.
- Sackeim, H., Greenberg, M. S., Weimen, A. L., Gur, R. C., Hungerbuhler, J. P., & Geschwind, N. (1982). Hemispheric asymmetry in the expression of positive and negative emotions: Neurologic evidence. *Archives of Neurology*, *39*, 210–218.
- Salavert, J., Caseras, X., Torrubia, R., Furest, S., Arranz, B., Dueñas, R., & San, L. (2007). The functioning of the Behavioral Activation and Inhibition Systems in bipolar I euthymic patients and its influence in subsequent episodes over an eighteen-month period. *Personality and Individual Differences*, *42*(7), 1323–1331.
- Santesso, D. L., Segalowitz, S. J., Ashbaugh, A. R., Antony, M. M., McCabe, R. E., & Schmidt, L. A. (2008). Frontal EEG asymmetry and sensation seeking in young adults. *Biological Psychology*, *78*, 164–172.
- Schaffer, C. E., Davidson, R. J., & Saron, C. (1983). Frontal and parietal electroencephalogram asymmetry in depressed and nondepressed subjects. *Biological Psychiatry*, *18*, 753–762.
- Schiff, B. B. & Lamon, M. (1989). Inducing emotion by unilateral contraction of facial muscles: A new look at hemispheric specialization and the experience of emotion. *Neuropsychologia*, *27*, 923–935.
- Schiff, B. B. & Lamon, M. (1994). Inducing emotion by unilateral contraction of hand muscles. *Cortex*, *30*, 247–254.
- Schmeichel, B. J., Crowell, A., & Harmon-Jones, E. (2016). Exercising self-control increases relative left frontal cortical activation. *Social Cognitive and Affective Neuroscience*, *11*, 282–288.
- Schöne, B., Schomberg, J., Gruber, T., & Quirin, M. (2016). Event-related frontal alpha asymmetries: Electrophysiological correlates of approach motivation. *Experimental Brain Research*, *234*(2), 559–567. doi:10.1007/s00221-015-4483-6
- Schutter, D. J. L. G. (2009). Transcranial magnetic stimulation. In E. Harmon-Jones & J. S. Beer (Eds.), Methods in social neuroscience (pp. 233–258). Guilford Press.
- Schutter, D. J. L. G. & Harmon-Jones, E. (2013). The corpus callosum: A commissural road to anger and aggression. *Neuroscience & Biobehavioral Reviews*, *37*, 2481–2488. [http://dx.doi.](http://dx.doi.org/10.1016/j.neubiorev.2013.07.013) [org/10.1016/j.neubiorev.2013.07.013](http://dx.doi.org/10.1016/j.neubiorev.2013.07.013)
- Schutter, D. J. L. G., van Honk, J., d'Alfonso, A. A. L., Postma, A., & de Haan, E.H.F. (2001). Effects of slow rTMS at the right dorsolateral prefrontal cortex on EEG asymmetry and mood. *Neuroreport*, *12*, 445–447.
- Shankman, S. A., Klein, D. N., Tenke, C. E., & Bruder, G. E. (2007). Reward sensitivity in depression: A biobehavioral study. *Journal of Abnormal Psychology*, *116*(1), 95–104
- Simons, J. S., Dvorak, R. D., Batien, B. D., & Wray, T. B. (2010). Event-level associations between affect, alcohol intoxication, and acute dependence symptoms: Effects of urgency, self-control, and drinking experience. *Addictive Behaviors*, *35*(12), 1045–1053. doi:10.1016/ j.addbeh.2010.07.001
- Siniatchkin, M., Kropp, P., & Gerber, W-D. (2000). Neurofeedback—The significance of reinforcement and the search for an appropriate strategy for the success of self-regulation. *Applied Psychophysiology and Biofeedback*, *25*, 167–175.
- Smith E. E., Cavanagh, J. F., & Allen, J. J. B. (2018). Intracranial source activity (eLORETA) related to scalp-level asymmetry scores and depression status. *Psychophysiology*, *55*(1), 119– 134.
- Smith, E. E., Zambrano-Vazquez, L., & Allen, J. J. B. (2016). Patterns of alpha asymmetry in those with elevated worry, trait anxiety, and obsessive-compulsive symptoms: A test of the
ASYMMETRIC FRONTAL CORTICAL ACTIVITY 257
- worry and avoidance models of alpha asymmetry. *Neuropsychologia*, *85*, 118–126. [https://doi.](https://doi.org/10.1016/j.neuropsychologia.2016.03.010) [org/10.1016/j.neuropsychologia.2016.03.010](https://doi.org/10.1016/j.neuropsychologia.2016.03.010)
- Smits, D. J. M. & Kuppens, P. (2005). The relations between anger, coping with anger, and aggression, and the BIS/BAS system. *Personality and Individual Differences*, *39*, 783–793.
- Spielberger, C. D. (1988). *State–trait anger expression inventory*. Psychological Assessment Resources.
- Spielberger, C. D., Reheiser, E. C., & Sydeman, S. J. (1995). Measuring the experience, expression, and control of anger. In H. Kassinove (Ed.), *Anger disorders: Definition, diagnosis, and treatment* (pp. 49–67). Taylor & Francis.
- Stewart, J. L. & Allen, J. J. (2018). Resting frontal brain asymmetry is linked to future depressive symptoms in women. *Biological Psychology*, *136*, 161–167.
- Stewart, J. L., Bismark, A. W., Towers, D. N., Coan, J. A., & Allen, J. J. B. (2010). Resting frontal EEG asymmetry as an endophenotype for depression risk: Sex-specific patterns of frontal brain asymmetry. *Journal of Abnormal Psychology*, *119*(3), 502–512.
- Stewart, J. L., Coan, J. A., Towers, D. N., & Allen, J. J. B. (2011). Frontal EEG asymmetry during emotional challenge differentiates individuals with and without lifetime major depressive disorder. *Journal of Affective Disorders*, *129*(1), 167–174. [https://doi.org/https://doi.org/](https://doi.org/https://doi.org/10.1016/j.jad.2010.08.029) [10.1016/j.jad.2010.08.029](https://doi.org/https://doi.org/10.1016/j.jad.2010.08.029)
- Stewart, J. L., Coan, J. A., Towers, D. N., & Allen, J. J. B. (2014). Resting and task-elicited prefrontal EEG alpha asymmetry in depression: Support for the capability model. *Psychophysiology*, *51*(5), 446–455.
- Strack, F. & Deutsch, R. (2004). Reflective and impulsive determinants of social behavior. *Personality and Social Psychology Review*, *8*(3), 220–247. doi:10.1207/s15327957pspr0803\_1
- Sutton, S. K. & Davidson, R. J. (1997). Prefrontal brain asymmetry: A biological substrate of the behavioral approach and inhibition systems. *Psychological Science*, *8*, 204–210.
- Teper, R. & Inzlicht, M. (2013). Meditation, mindfulness and executive control: The importance of emotional acceptance and brain-based performance monitoring. *Social, Cognitive, and Affective Neuroscience*, *8*(1), 85–92. doi:10.1093/scan/nss045
- Terzian, H. & Cecotto, C. (1959). Determination and study of hemisphere dominance by means of intracarotid sodium amytal injection in man: II. Electroencephalographic effects. *Bollettino della Societa Italiana Sperimentale*, *35*, 1626–1630.
- Thibodeau, R., Jorgensen, R. S., & Kim, S. (2006). Depression, anxiety, and resting frontal EEG asymmetry: A meta-analytic review. *Journal of Abnormal Psychology*, *115*(4), 715–729. doi:10.1037/ 0021-843X.115.4.715.
- Tomarken, A. J. & Davidson, R. J. (1994). Frontal brain activation in repressors and nonrepressors. *Journal of Abnormal Psychology*, *103*(2), 339–349. doi:10.1037/ 0021-843X.103.2.339
- Tomarken, A. J., Davidson, R. J., Wheeler, R. E., & Doss, R. (1992). Individual differences in anterior brain asymmetry and fundamental dimensions of emotion. *Journal of Personality and Social Psychology*, *62*, 676–687.
- Urosevic, S., Abramson, L. Y., Alloy, L. B., Nusslock, R., Harmon-Jones, E., Bender, R., & Hogan, M. E. (2010). Increased rates of events that activate or deactivate the Behavioral Approach System, but not events related to goal attainment, in bipolar spectrum disorders. *Journal of Abnormal Psychology*, *119*, 610–615.
- Valiente, C., Eisenberg, N., Smith, C. L., Reiser, M., Fabes, R. A., Losoya, S., ... Murphy, B. C. (2003). The relations of effortful control and reactive control to children's externalizing
258 EDDIE HARMON-JONES, TAYLOR POPP, AND PHILIP A. GABLE
- problems: A longitudinal assessment. *Journal of Personality*, *71*(6), 1171–1196. doi:10.1111/ 1467-6494.7106011
- van de Laar, M. C., Licht, R., Franken, I. H. A., & Hendriks, V. M. (2004). Event-related potentials indicate motivational relevance of cocaine cues in abstinent cocaine addicts. *Psychopharmacology*, *177*, 121–129.
- Verona, E., Sadeh, N., & Curtin, J. J. (2009). Stress-induced asymmetric frontal brain activity and aggression risk. *Journal of Abnormal Psychology*, *118*, 131–145.
- Wacker, J., Chavanon, M. L., Leue, A., & Stemmler, G. (2008). Is running away right? The behavioral activation-behavioral inhibition model of anterior asymmetry. *Emotion*, *8*(2), 232– 249. doi:10.1037/1528-3542.8.2.232
- Wacker, J., Chavanon, M. L., & Stemmler, G. (2010). Resting EEG signatures of agentic extraversion: New results and meta-analytic integration. *Journal of Research in Personality*, *44*(2), 167–179. doi:10.1016/j.jrp.2009.12.004
- Wacker, J., Heldmann, M., & Stemmler, G. (2003). Separating emotion and motivational direction in fear and anger: Effects on frontal asymmetry. *Emotion*, *3*, 167–193.
- Wacker, J., Mueller, E. M., Pizzagalli, D. A., Hennig, J., & Stemmler, G. (2013). Dopamine-D2 receptor blockade reverses the association between trait approach motivation and frontal asymmetry in an approach-motivation context. *Psychological Science*, *24*, 489–497.
- Whiteside, S. P., Lynam, D. R., Miller, J. D., & Reynolds, S. K. (2005). Validation of the UPPS impulsive behaviour scale: A four-factor model of impulsivity. *European Journal of Personality*, *19*(7), 559–574. doi:10.1002/per.556
- Wiedemann, G., Pauli, P., Dengler, W., Lutzenberger, W., Birbaumer, N., & Buchkremer, G. (1999). Frontal brain asymmetry as a biological substrate of emotions in patients with panic disorders. *Archives of GENERAL PSYCHIATRY*, *56*(1), 78–84.
- Young, P. T. (1943). *Emotion in man and animal: Its nature and relation to attitude and motive*. John Wiley and Sons.
- Zapolski, T. C., Cyders, M. A., & Smith, G. T. (2009). Positive urgency predicts illegal drug use and risky sexual behavior. *Psychology of Addictive Behaviors*, *23*(2), 348. doi:10.1037/ a0014684
- Zinner, L. R., Brodish, A. B., Devine, P. G., & Harmon-Jones, E. (2008). Anger and asymmetric frontal cortical activity: Evidence for an anger-withdrawal relationship. *Cognition & Emotion*, *22*, 1081–1093.
## [CHAPTER 12](#page-6-4)
# [OSCILL ATORY ACTIVIT Y IN](#page-6-4) [SENSORIMOTOR FUNCTION](#page-6-4)
Bernadette C. M. van WIJK
# **12.1 Understanding the sensorimotor system**
Movement is quintessential for most living organisms including humans. It is through movement that we feed ourselves, reproduce, communicate, perceive, and affect the external world. Most of our daily movements are performed without giving them much thought. We lift our arm to reach for a cup of coffee, grasp our fingers around it with enough force to hold the cup, and bring it to our mouth in order to drink without spilling—all seemingly without any effort. Even this arguably simple action requires transformation of an action goal into a movement trajectory, activation and deactivation of several muscle groups at appropriate moments in both space and time, and relies on accurate integration of visual information on the shape and position of the cup, proprioceptive input from muscles and joints on position and velocity of the limbs, and haptic feedback from which we can infer the cup's weight, to plan and adjust muscle activations. Fortunately, we can acquire complex motor skills through practice. We can learn how to coordinate our finger movements to efficiently type a text on a computer keyboard, or even to play the most virtuoso piano pieces.
The sensorimotor system is the network of motor and sensory regions in the brain and spinal cord thought to be involved in the planning, initiation, and execution of movements. In humans, it comprises primary somatosensory cortex (S1), primary motor cortex (M1), dorsal and ventral premotor cortex (PMd, PMv), (pre-)supplementary motor area (SMA), cingulate motor areas (CMA), cerebellum, the basal ganglia, several nuclei in brainstem and thalamus, motoneurons and interneurons in the spinal cord, and muscle afferents (Figure 12.1). Roughly speaking, one can distinguish a medial pathway of fiber tracts descending from cortex and brainstem nuclei down the spinal
260 Bernadette C. M. van Wijk
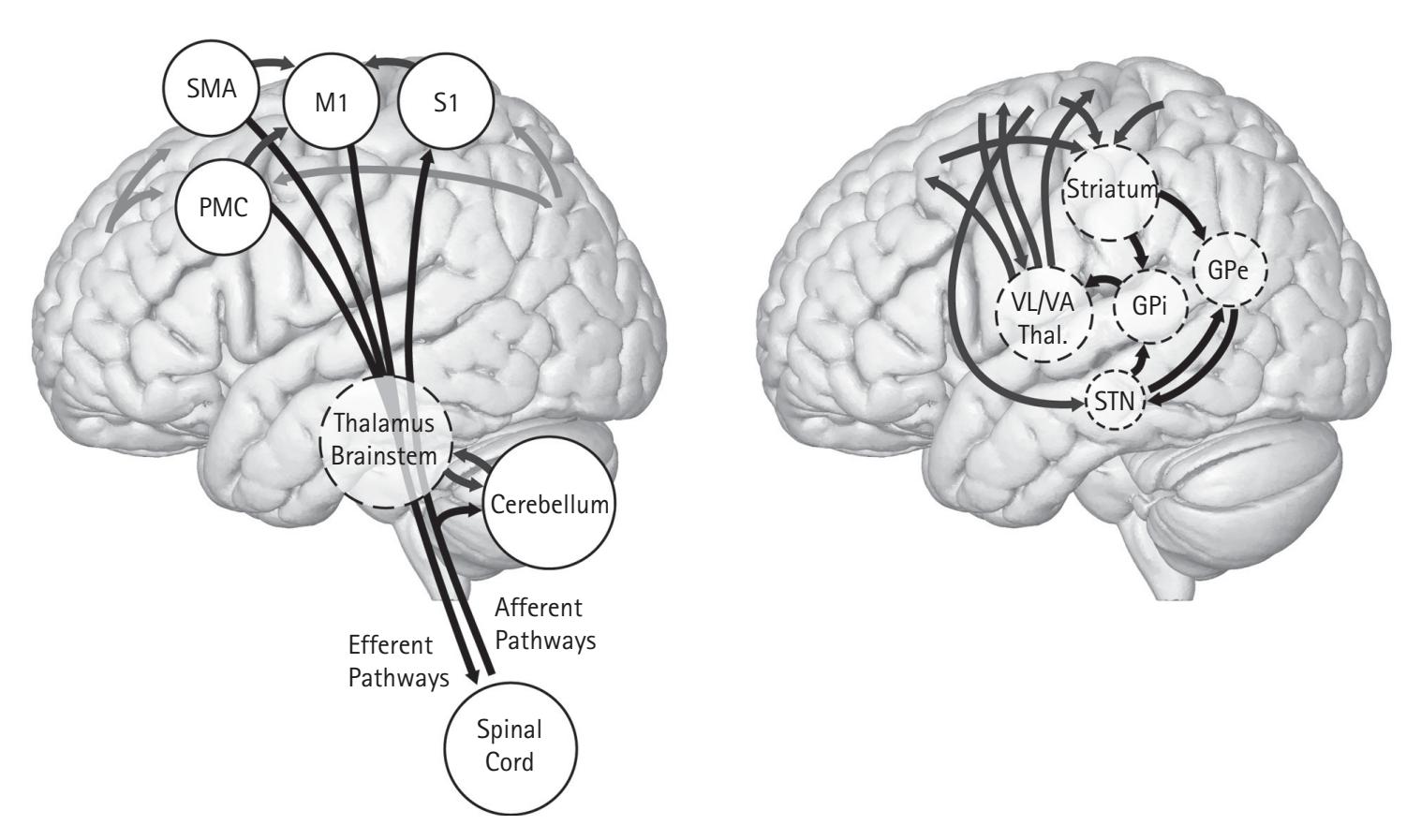
**Figure 12.1** Schematic overview of major cortical and subcortical pathways that comprise the sensorimotor system. Left: primary and secondary motor cortex project directly to the spinal cord and via brainstem nuclei. Afferent proprioceptive information travels to primary somatosensory cortex via thalamus and enters the cerebellum directly. Right: The basal ganglia consist of the striatum, internal and external pallidum (GPi, GPe), and subthalamic nucleus (STN). Together with the thalamus they form circuits with various cortical regions, of which the ventral lateral and ventral anterior thalamus (VL, VA) project to primary and secondary motor cortex.
cord that innervate axial muscles for the regulation of posture and balance, and a lateral tract innervating distal muscles. The sensorimotor system has a bilateral organization, with most corticospinal tracts crossing at the level of the medulla. This suggests that movements of the right arm and leg are primarily controlled by the left hemisphere, and vice versa. Movements and actions are intricately linked with perception and cognition; therefore, the sensorimotor system must uphold strong ties with other circuits. As such, the distinction between systems is not always clear and some sensorimotor regions have been ascribed more cognitive roles.
As much as one would like to understand how a gymnast performs a twisting somersault, the study of (supraspinal) neural control of movement in laboratory settings is typically restricted to what is often referred to as "simple" uni- or bimanual movements like finger tapping or isometric force generation. Electroencephalography (EEG), magnetoencephalography (MEG), and electrocorticography (ECoG) are predominantly sensitive to synchronous synaptic transmission in cortical regions, while electromyography (EMG) may provide insight into the activation of motoneurons in the spinal cord via the spread of action potential currents that can be picked up non-invasively with electrodes placed on the skin over the muscle belly. Increasing use of deep brain stimulation (DBS) for the treatment of movement disorders allows for invasively recording local field potentials (LFPs) from basal ganglia and thalamic OSCILLATORY ACTIVITY IN SENSORIMOTOR FUNCTION 261
structures in humans. It is even possible to combine recording techniques in a single experiment to investigate distant interactions between different parts of the sensorimotor system. For example, simultaneous use of EEG/MEG and EMG allows for the detection of functional interactions between cortex and spinal cord, and invasive LFP recordings from DBS electrodes can be combined with non-invasive EEG or MEG to detect functional interactions between cortex and basal ganglia structures like the subthalamic nucleus (STN) and internal pallidum (GPi). Performed movements can be co-registered via button-presses, force sensors, trackpads, joy sticks, or motioncapturing systems. By investigating how recorded neural signals change during the experimental task or due to pathology one could relate oscillatory activity to motor function.
Movement-related neural population activity appears in several frequency bands (Figure 12.2). Many studies contributed to understanding the functional role of these frequency bands in individual sensorimotor regions. Via measures of coupled oscillatory activity (e.g., *coherence*) one could get a sense of functional connectivity within the system. This chapter highlights several research findings and (ongoing) debates on which we build our current knowledge. While it covers many topics, it is meant as introductory text rather than an exhaustive literature review. Although we have studied oscillations in sensorimotor function for many decades, it is exciting to see that the field is still evolving with new technologies, signal processing techniques, and novel experimental paradigms.
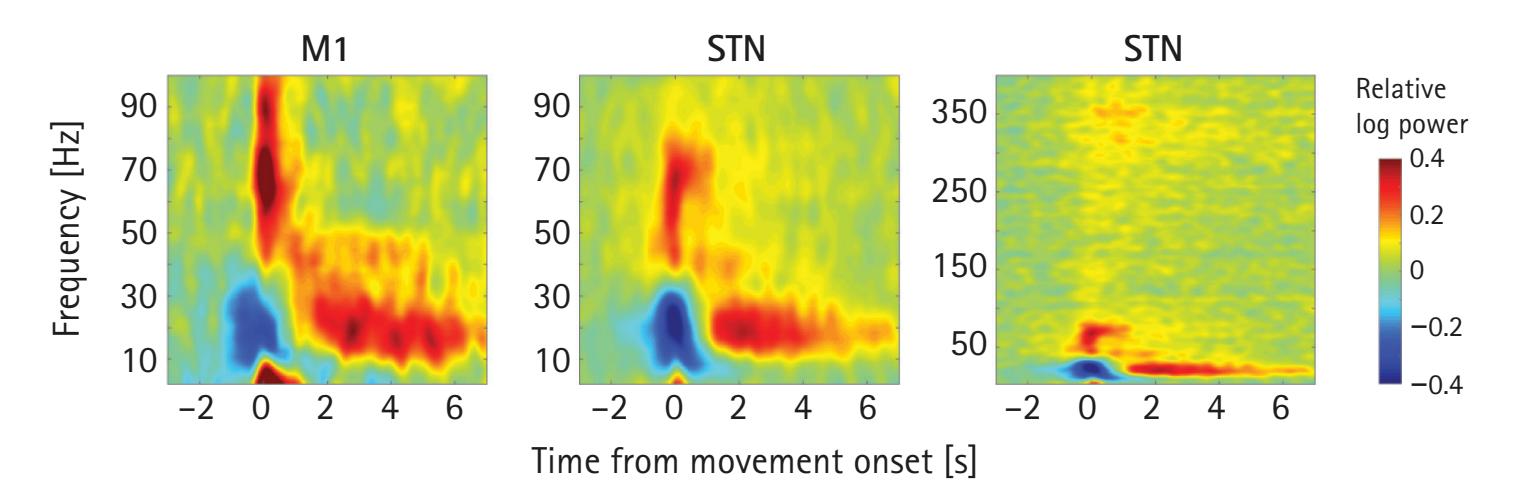
**Figure 12.2** Movement-related time-frequency spectra for primary motor cortex (M1) and subthalamic nucleus (STN). Panels show the relative change in spectral power with respect to a pre-movement baseline window. Participants performed a simple self-paced button press movement with three fingers simultaneously at time point 0. Beta power starts to decrease before movement onset (ERD) and shows a clear post-movement rebound (ERS). Gamma power increases around movement onset. In STN, another movement-related increase with smaller amplitude can be observed in the range for high-frequency oscillations (HFOs). Note how timefrequency modulations look very similar for M1 and STN, suggesting generic principles of information processing.
Spectra are based on MEG and DBS-LFP recordings from eleven Parkinson's disease patients on dopaminergic medication taken from Litvak et al., 2012.
262 Bernadette C. M. van Wijk
# **12.2 A traditional view on frequency bands**
Ever since the first recordings, researchers have divided EEG/MEG time series into frequency bands that are presumed to have their own functional roles. This section focuses on the properties of frequency bands that are thought to be central to sensorimotor function.
#### **12.2.1 The Difference Between Alpha, Mu, and Beta**
The alpha rhythm was the first rhythm observed by Berger (1929). Soon after, it was discovered that the alpha rhythm is suppressed when closing the eyes, has its origin in the occipital lobes (Adrian & Matthews, 1934), and that another alpha rhythm can be observed close to the central sulcus that, together with a beta rhythm, is suppressed upon tactile stimulation (Jasper & Andrews, 1938). Later studies showed that the central rhythms are also modulated by passive, voluntary, and imagined movements (Chatrian et al., 1959; Gastaut, 1952; Jasper & Penfield, 1949). The alpha rhythm close to the central sulcus (or "Rolandic fissure") was named *mu*—after the arch-like shape of the oscillation. However, in the current literature mu and alpha are used interchangeably. Mu/ alpha oscillations are usually defined to have a peak frequency between 8–13 Hz. Beta oscillations are considered to occur within the approximate range of 13–30 Hz. Both alpha/mu and beta oscillations show a distinctive decrease in amplitude prior to and during movement execution (event-related desynchronization, ERD), followed by a rebound that exceeds baseline after the movement has been terminated (event-related synchronization, ERS) (Pfurtscheller & Lopes Da Silva, 1999). Still, dissimilarities in time course, spatial origin, and coupling to other regions indicate that the two bands are functionally distinct.
Beta ERD might start as early as 2 s before movement initiation and is often thought to reflect a general state of motor preparation (Neuper & Pfurtscheller, 2001). It starts over sensorimotor cortex contralateral to the moving hand and becomes bilateral during movement. Alpha/mu ERD starts a bit later in time and is spatially more diffuse and somatotopically less specific (Crone et al., 1998b). Beta ERS is often more pronounced and occurs at a shorter latency compared alpha ERS (Alegre et al., 2003; Erbil & Ungan, 2007; Pfurtscheller et al., 1996; Salmelin & Hari, 1994). The two rhythms are likely to originate from distinct sources as different source localization methods ascribed beta modulations to precentral (motor) cortex and mu/alpha modulations to postcentral (somatosensory) cortex (Cheyne et al., 2003; Ritter et al., 2009; Salmelin et al., 1995; Salmelin & Hari, 1994). As explained in the subsequent sections, the beta band often shows the most specific modulations with experimental conditions and pathology OSCILLATORY ACTIVITY IN SENSORIMOTOR FUNCTION 263
and dominates the functional connectivity profile for sensorimotor cortex. For these reasons, beta oscillations are considered most associated with motor control.
#### **12.2.2 A Prominent Role for Beta Oscillations**
The primary functional role of beta oscillations seems to be the facilitation and inhibition of movements. Beta ERD already starts during the movement preparation phase and appears stronger when the action that needs to be prepared is known in advance. The ERD is lateralized with stronger suppression over contralateral M1 when the response hand is known, also resulting in faster reaction times (Doyle et al., 2005b; van Wijk et al., 2009). On the other hand, ERS only appears after the movement has been terminated, and therefore has been proposed to reflect a period of inactivation to recover from previous activation (Pfurtscheller et al., 1996), or processing of afferent somatosensory information (Cassim et al., 2001). Chen and colleagues (1998) tracked the time course of corticospinal excitability around self-paced and instructed movements using transcranial magnetic stimulation. Pulses were delivered at different time points around movement onset to see how the amplitude of motor evoked potentials varied during the time windows of ERD and ERS. An increase in corticospinal excitability was found in the final 100 ms of the pre-movement preparation phase and around 100 ms after movement onset, which are time periods during which ERD is often strongest. By contrast, a decrease in corticospinal excitability was found between 500 and 1000 ms after movement, which is around the time of ERS.
Beta oscillations are not simply an idling state, but also have a functional impact on the initiation and stabilization of motor output. Movements are performed more slowly when initiated during periods of high-amplitude beta oscillations in the ongoing EEG (Gilbertson et al., 2005). Entrainment of cortical beta oscillations by transcranial alternating-current stimulation at 20 Hz has a similar effect (Pogosyan et al., 2009). Cortico-spinal beta phase synchronization increases when the current motor output needs to be maintained (van Wijk et al., 2009), for example, in anticipation of upcoming perturbations to finger position (Androulidakis et al., 2007a). This implies that both a down- and up-regulation of beta oscillations is employed by the nervous system to tune motor output.
What happens at a neurobiological level that determines the amplitude of beta oscillations? Motor cortical architecture consists of intricately and reciprocally connected excitatory pyramidal cells and inhibitory interneurons within and across layers (Keller, 1993). In order to determine the contribution of individual receptor types to network activity they can be activated or blocked with pharmacological agents in in vitro slice preparations of animal cortex. This revealed GABAA receptors to be critical for the generation of beta oscillations together with an influence of gap junctions, but not AMPA receptors (Yamawaki et al., 2008). There are strong indications that beta oscillations originate in layer V while also clearly present in layer II. IPSPs on layer 5 pyramidal cells are phase locked with the LFP beta oscillation, as is the spiking of 264 Bernadette C. M. van Wijk
pyramidal cells but at much sparser rates (Lacey et al., 2014). The dependence of beta oscillation amplitude on GABAA receptors has also been established through in vivo pharmacological studies in humans. After administration of benzodiazepines, a class of GABAergic drugs often prescribed as anticonvulsants, sedatives, or muscle relaxants, spectral beta power in EEG/MEG appears enhanced (Baker & Baker, 2003; Hall et al., 2010; Jensen et al., 2005). Along these lines, computational modelling work suggests that stronger synaptic inputs between pyramidal cells in different layers might underlie the beta suppression that is observed during movement (Bhatt et al., 2016).
Despite the prominence of beta band oscillations in sensorimotor function, movement-related modulations only seem to encode general motor aspects. More forceful movements induce stronger alpha/mu and beta ERD (Mima et al., 1999; Stančák et al., 1997; Stančák & Pfurtscheller, 1996) as do movements that are performed with a higher frequency (Toma et al., 2002) or involving more complex sequences (Hummel et al., 2003; Manganotti et al., 1998). Movements with more muscle mass involved do not influence ERD but rather lead to stronger beta ERS (Pfurtscheller et al., 1998; Stančák et al., 2000). Movement duration has little effect on either ERD or ERS (Cassim et al., 2000; Stančák & Pfurtscheller, 1996). It is however difficult to pinpoint ERD and ERS patterns to specific motor parameters.
#### **12.2.3 Prokinetic Gamma**
To find a mechanistic link between beta oscillations and the control of movement trajectory and muscle force, it can be useful to consider the behavior of individual neurons. Pyramidal tract neurons (PTNs) in infragranular layers project to motoneurons of individual muscles and groups of muscles in the spinal cord, and appear to be functionally organized in small clusters (Asanuma et al., 1979). They only form a minority of cells in motor cortex and form intricate connections with other neurons within and between cortical modules that together encode movement patterns (Keller, 1993). Microelectrode recordings in sensorimotor cortices of the macaque monkey revealed spikes of individual neurons to be phase-locked to the LFP beta oscillation during time periods when the oscillation is well pronounced (Baker et al., 1997; Denker et al., 2007; Murthy & Fetz, 1996a). Although the phase locking of individual PTNs to the beta oscillation may only be weak, summation over a population of neurons can give a clearer picture (Baker et al., 2003). We also know that the encoding of parameters such as hand position, direction of motion, velocity, and force emerges from the joint firing rates of a group of neurons that are individually tuned (Ashe & Georgopoulos, 1994; Fu et al., 1995; Georgopoulos et al., 1986; Moran & Schwartz, 2017; Paninski et al., 2004). This is termed *population coding*.
When movements are executed, phase locking of spikes with the beta oscillation drops and spike rates strongly increase (Baker et al., 2001; Spinks et al., 2008). There is a crude inverse correlation between spike rates and LFP beta power. Spike rates reach frequencies above 30 Hz (Baker et al., 2001; Grammont and Riehle, 2003) and OSCILLATORY ACTIVITY IN SENSORIMOTOR FUNCTION 265
may well correspond to the brief increases in gamma power (~30–100 Hz) that can be observed in EEG and MEG recordings in a time window around movement onset (Cheyne et al., 2008; Muthukumaraswamy, 2010; Ohara et al., 2001; Pfurtscheller et al., 1993; Pfurtscheller & Neuper, 1992). Unlike the alpha/mu and beta ERD, the increase in gamma only occurs in the hemisphere contralateral to the moving body part and is somatotopically more focused (Crone et al., 1998a; Miller et al., 2007; Szurhaj et al., 2005). Some studies report the gamma amplitude increase to vary with movement direction in invasive recordings (Leuthardt et al., 2004; Rickert et al., 2005). However, it remains to be seen whether gamma power in EEG and MEG recordings has the same specificity. Taken together, one may hypothesize that the beta oscillation inhibits, or constrains, neuronal spiking. That is, a suppression of the beta rhythm can lead to an increase in excitability of individual neurons that together encode movement parameters.
### **12.2.4 High-Frequency Oscillations**
The latest addition to the repertoire of movement-related oscillations is a spectral component with a clear peak in the 150–400 Hz frequency range, aptly coined *highfrequency oscillations* (HFO). HFO have been observed in LFP recordings from DBS electrodes in the STN and internal pallidum. They are of interest to sensorimotor function as they show a characteristic increase in amplitude during movement (Foffani et al., 2003; Litvak et al., 2012; López-Azcárate et al., 2010; Tan et al., 2013; Tsiokos et al., 2013), like the gamma band. Their peak frequency is modulated by dopaminergic medication (López-Azcárate et al., 2010; Özkurt et al., 2011; van Wijk et al., 2016) and indicative of tremor symptoms in patients with Parkinson's disease (Hirschmann et al., 2016). Yet, a similar movement-related HFO component in the cortex has not been reported although this may simply be due to the poor signal-to-noise ratio of commonly used EEG/MEG compared to more focal, invasive techniques.
# **12.3 Coherence as a measure of functional connectivity within the sensorimotor system**
Any understanding of sensorimotor function will not be complete if the information exchange between regions that comprise the sensorimotor system is ignored. Rhythmic synchronization in the form of oscillations has been recognized as a means by which neural populations selectively gate their sensitivity to input from other populations (Fries, 2005). The degree of synchronization between neural populations can be estimated by computing *coherence* between time series as a measure of functional connectivity. This measure can be understood as spectral counterpart of conventional correlation.
266 Bernadette C. M. van Wijk
## **12.3.1 Cortico-Spinal Coherence**
Corticospinal coherence, also called corticomuscular coherence, refers to the synchronization between oscillations in cortex and motoneuron activity in the spinal cord. Firing of motoneurons yields motor unit action potentials that induce contraction of muscle fibers. Repetitive firing is necessary in order to build up force. The rate at which this occurs ranges from 6 Hz in rest to 35 Hz during forceful isometric contractions and bursts of 80–120 Hz in case of rapid, ballistic movements (Freund, 1983). As such, corticospinal coherence may reflect whether synchronized activity in cortex also reaches the muscles.
Several studies report weak but significant beta-band coherence between the EMG of hand or foot muscles and EEG over contralateral sensorimotor regions during sustained isometric muscle contractions (Conway et al., 1995; Gross et al., 2000; Halliday et al., 1998; Salenius et al., 1997; van Wijk et al., 2012). Coherence levels increase for muscle contractions with higher force levels (Chakarov et al., 2009; Witte et al., 2007) and peak frequencies shift into the gamma range during maximal force production (Brown et al., 1998; Mima et al., 1999). Task-dependent coherence has also been found for the EEG with different muscle groups, thereby forming functional synergies (Zandvoort et al., 2019), or between EMG recordings of different muscles themselves (Boonstra et al., 2016). While beta-band corticospinal coherence diminishes during movement (Baker et al., 1997; Kilner et al., 2000), alpha-band coherence between active muscle groups increases (Boonstra et al., 2009). Typically, no significant coherence can be observed in rest unless a strong tremor is present (Hellwig et al., 2001).
Corticospinal beta coherence can be modulated by cognitive factors. The division of attention during dual task performance decreases coherence levels (Johnson et al., 2011; Kristeva-Feige et al., 2002; Safri et al., 2007), whereas task instructions to maintain force output at a target level with high precision lead to increased coherence (Kristeva et al., 2007). Using a pre-cued choice reaction time task, Van Wijk and colleagues (2009) demonstrated that corticospinal coherence can be up-regulated in anticipation of an upcoming movement decision. Key to their experimental paradigm was the preactivation of muscles in each trial via a precision grip before stimuli were displayed. This led to a build-up of corticospinal coherence that allows for modulations to be observable. After presentation of a warning cue of the likely upcoming response hand, corticospinal synchronization increased for the non-selected hand, while cortical beta power decreased for the selected hand. These and other findings jointly suggest that the role of beta oscillations to facilitate or inhibit movements extends to the level of the spinal cord.
Does corticospinal coherence reflect mere entrainment of motoneurons by cortical output? Feedback signals from muscle afferents ascend the spinal cord to somatosensory cortex, which through strong connections with primary motor cortex, closes the corticospinal loop. Riddle and Baker (2005) sought to tackle this question experimentally by cooling subjects' arms. Cooling caused an additional time delay (inferred from phase-frequency regression) that was about twice the conduction time in one direction. OSCILLATORY ACTIVITY IN SENSORIMOTOR FUNCTION 267
The authors therefore concluded that both ascending and descending pathways contribute to the occurrence of corticospinal coherence. One may determine the directionality of coupling by using measures such as Granger causality. This similarly revealed significant contributions of both ascending and descending pathways (Witham et al., 2011). It is worth noting that corticospinal coherence does not strictly follow modulations of cortical power. Baker and Baker (2003) demonstrated this by recording subjects before and after intake of diazepam, a benzodiazepine that enhances inhibitory post-synaptic potentials via GABAA receptors. EEG beta power doubled in amplitude, but corticospinal coherence was little altered. Interactions between cortex and spinal cord might therefore be more complex than a simple one-way drive.
## **12.3.2 Cortico-Subcortical Coherence**
With EEG and MEG being most sensitive to cortical sources, it is easy to forget the contribution of more deeply located brain structures. Many of these are highly relevant for sensorimotor and cognitive functions. DBS treatment allows for invasively recording electrophysiological activity from subcortical structures in humans. The subthalamic nucleus (STN) and internal pallidum (GPi) are primary targets for the treatment of Parkinson's disease and dystonia, the pedunculopontine nucleus (PPN) for postural instability and gait freezing, and the ventrolateral thalamus (including ventral intermediate nucleus) for tremor. It is possible, albeit challenging, to combine LFP recordings from DBS electrodes with simultaneous EEG or MEG to study corticosubcortical interactions.
Early simultaneous LFP-MEG studies sought to map functional connectivity with cortical regions across different frequency ranges during rest. Litvak and colleagues (2011) and Hirschmann and colleagues (2011) showed converging evidence for the presence of two spatially distinct and frequency-specific networks for the STN and ipsilateral cortical areas: alpha-band coherence with temporoparietal cortex and beta-band coherence with pre-motor cortex. Coherence values for these sources were little altered with dopaminergic medication. Using directionality analysis, cortical activity was found to drive STN activity for both frequency bands (Litvak et al., 2011). Both research labs followed up on these studies by investigating movementrelated coherence but found more conflicting results. Litvak and colleagues (2012) reported an increase in gamma band coherence during movement execution that was further increased by dopaminergic mediation. Beta coherence increased during the post-movement beta rebound period but was unaltered by medication. In a separate study, they describe a reduction of alpha-band coherence during movement that was more pronounced with medication (Oswal et al., 2013). By contrast, Hirschmann and colleagues (2013) found that medication reduced beta-band coherence during movement but not alpha.
Simultaneous LFP-MEG recordings identified functional networks also for other subcortical structures. Activity in PPN appeared coherent with that of the brainstem
268 Bernadette C. M. van Wijk
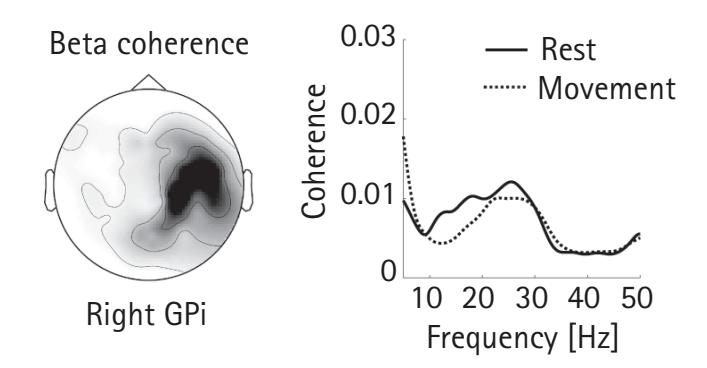
**Figure 12.3** Beta band coherence between the right internal pallidum (GPi) and ipsilateral sensorimotor cortex. Left: Topography with darker colors indicating stronger coherence values. Right: Coherence is reduced during movement compared to rest.
Both panels are based on MEG and DBS-LFP recordings from eight dystonia patients taken from Van Wijk et al., 2017.
and cingulate cortex in the alpha band, and with medial cortical motor areas in the beta band (Jha et al., 2017). For GPi, coherence was found with temporal cortex in the theta band, cerebellum in the alpha band, and sensorimotor cortex in the beta band (Neumann et al., 2015). This study was conducted in dystonia patients, for whom disease severity significantly correlated only with theta band coherence. Beta-band coherence was unrelated to symptoms but showed a movement-related reduction (van Wijk et al., 2017; see Figure 12.3). The lack of clear alterations of cortico-subcortical coherence by medication or correlation with clinical symptoms suggests that this form of functional coupling might be physiological rather than disease-related. Experimental paradigms with more refined task designs will be needed to unravel their functional roles.
#### **12.3.3 Cortico-Cortical Coherence**
Many motor tasks call upon the coordinated activation of multiple cortical regions. Researchers have used coherence analysis with the aim to find traces of functional coupling between EEG/MEG time series recorded at different locations. Some of these findings confirmed inter-regional coupling patterns as one would expect from postulated sensorimotor functions of individual brain regions. For example, the observation of higher coherence values between sensorimotor cortex and mesial premotor areas for internally compared to externally paced movement is in line with the presumed involvement of SMA in self-initiated movements (Gerloff et al., 1998; Serrien, 2008). Other findings are arguably more open for interpretation, like the increased level of interhemispheric coherence between sensorimotor regions during more complex unimanual and bimanual tasks (Gerloff et al., 1998; Gross et al., 2005; Manganotti et al., 1998; Mima et al., 2000), or the observed gamma band coherence between cerebellar hemispheres during bimanual finger tapping (Pollok et al., 2007). Notably, corticocortical coherence can be used to reveal the integration of information from sensory modalities during motor tasks. Classen and colleagues (1998) demonstrated that betaband coherence between motor and visual cortex is higher when participants make OSCILLATORY ACTIVITY IN SENSORIMOTOR FUNCTION 269
use of visual information to perform a visuomotor tracking task compared to when the visual stimulus is a mere distractor. Similarly, significant alpha-band coherence between auditory cortices and the motor network can be found when finger tapping is paced by a metronome (Pollok et al., 2005).
Coherence analysis between EEG/MEG time series is easily prone to volume conduction: multiple electrodes or sensors pick up the same neural activity leading to an overestimation of functional connectivity. This prompted the development of alternative connectivity measures like the *imaginary part of coherency* (Nolte et al., 2004), where the real part of the cross-spectrum is ignored as it may contain volume conduction artifacts. The authors applied this measure to EEG data of a unimanual finger tapping task and demonstrated a weak but significant 20 Hz coupling from contralateral to ipsilateral sensorimotor cortex in the time period before movement onset and in the reverse direction after movement. Another measure is the *phase lag index* (Stam et al., 2007), which eliminates instantaneous coupling by looking at the asymmetry of the relative phase distribution. Hillebrand and colleagues (2012) showed that this measure removes volume conduction effects that are still present after projecting MEG data to source space and identified a strongly connected sensorimotor network in the beta band. The disadvantage of these measures is that any true coupling with zero time-lag is also ignored, therefore their estimates are on the conservative side.
Invasive recordings reduce the problem of volume conduction if electrodes can be placed sufficiently far apart. Murthy and Fetz (1996b) studied the occurrence of synchronized oscillations in LFP signals from bilateral sensorimotor areas in the macaque monkey. Oscillations occurred spontaneously at rest but only infrequently. They appeared more often during exploratory arm movements with fine use of the fingers, during which they were frequently synchronized between M1 and S1, and between bilateral M1s. Both occurred at near zero time-lags. Oscillations, however, did not seem to occur at consistent points in time related to the movements. Other studies did observe a systematic increase in synchronous oscillations between M1, S1, and premotor areas of the same hemisphere or between bilateral M1s around or before movement onset in more standardized tasks (Cardoso de Oliveira et al., 2001; Ohara et al., 2001; Sanes & Donoghue, 1993), therefore providing support for the involvement of oscillations in functional coupling between cortical areas.
# **12.4 Long-term changes in oscillatory activity**
Measures of sensorimotor beta oscillations appear to be highly consistent within individuals across repeated recording sessions (Espenhahn et al., 2017). However, their characteristics might change over time due to several factors.
270 Bernadette C. M. van Wijk
## **12.4.1 Altered Oscillations Due to Development and Aging**
Physiological changes occur throughout our body as we grow older. Alterations in grey matter volume, myelination, structural connectivity, neurotransmitters, receptors, and skull conductivity (when recording EEG) potentially affect amplitudes and peak frequencies of neural oscillations. In a cross-sectional study, Heinrichs-Graham and colleagues (2018) investigated the age-dependency of movement-related oscillations by measuring MEG of 57 healthy participants between the ages of 9 and 75 years. Absolute (baseline) beta power showed a quadratic relation with age, with smallest values for young adults, somewhat larger values for children, and clearly largest values for older adults. The magnitude of beta ERD linearly increased across all ages, whereas postmovement ERS was most pronounced for young adults. Similar patterns were found by other studies (Gaetz et al., 2010; Schmiedt-Fehr et al., 2016) that also reported a reduction of peak frequency for ERD (Rossiter et al., 2014) or ERS (Espenhahn et al., 2019) in older adults. Gamma ERS around movement onset has been reported to decrease in amplitude from childhood to adolescence (Trevarrow et al., 2019). While gamma ERS typically only occurs in contralateral sensorimotor cortex in adults, it may also be observed over ipsilateral cortex in younger children. Huo and colleagues (2011) reported ipsilateral gamma ERS for 12 out of 20 children in the 6–9-year-old age group and significantly fewer instances for older age groups. These findings are likely related to maturation of the corpus collosum and development of transcallosal inhibition that still continues at that age (Müller et al., 1997). Changes in oscillatory activity are hence evident throughout the lifespan; this should be considered when the experimental design includes between-group comparisons.
#### **12.4.2 Altered Oscillations Due to Learning**
On short time scales, oscillatory activity may depend on experience in the context of sensorimotor learning. Synaptic plasticity can lead to a strengthening or weakening of synaptic transmissions that may affect the amplitude of oscillations at a neural population level. Such reorganization has been observed during the course of learning new visuomotor tracking tasks or bimanual coordination patterns.
Tan and colleagues (2014) showed that the magnitude of post-movement beta ERS depends on kinematic error in a reaching task with rotational perturbations. In these experiments, single-trial beta ERS was negatively correlated with the angular discrepancy between the target movement trajectory and the actual performed trajectory. This effect was strongest when the perturbation angle was constant over trials compared to random. Hence, post-movement beta ERS does not merely reflect afferent feedback of the performed movement; rather, it represents a combination of prediction error and uncertainty of expected sensory consequences (Tan et al., 2016). Alayrangues and OSCILLATORY ACTIVITY IN SENSORIMOTOR FUNCTION 271
colleagues (2019) suggested that reorganization of the internal representation itself is not reflected by the post-movement ERS but by lower beta amplitudes during the preparatory period of movements in the *next* trial.
Motor skill learning is also associated with stronger beta ERD (Andres et al., 1999; Boonstra et al., 2007) and ERS (Moisello et al., 2015) in sensorimotor cortex, and more pronounced alpha band modulations in the cerebellum (Houweling et al., 2008) during task performance. More widespread changes in spectral power may also occur in these frequency bands that are stronger in young compared to older adults (Rueda-Delgado et al., 2019). Learning bimanual patterns impacts on functional connectivity within the sensorimotor network. In a study by Andres et al. (1999), healthy adult participants performed a 30-minute training session during which they learned to fuse two overlearned unimanual finger-tapping sequences into a new bimanual sequence. Interhemispheric coherence between sensorimotor regions in the alpha and beta band was increased during early stages of the training phase and decreased again after the bimanual sequence was learned. Interhemispheric interactions might be initially recruited to learn a new bimanual coordination pattern but are seemingly less needed after the pattern has been acquired. By contrast, Houweling and colleagues (2010) showed that the time course of bimanual learning is reflected in the build-up of corticospinal phase synchronization. There, it appears as if the synchronization is needed to perform the task adequately.
Changes in oscillatory activity can also be observed directly after a training session in the amplitude of ongoing beta oscillations. Espenhahn and colleagues (2019) recorded EEG before and after a 30-minute training session of a unimanual visuomotor tracking task. Absolute beta power during rest was significantly higher after training and returned to pre-training levels the following day. A similar effect was found by Moisello and colleagues (2015) and was suggested to reflect a reduction in cortical excitability after extended use. It would be of interest to conduct more longitudinal studies to see whether learning induces long-lasting changes to oscillatory activity or whether the system returns to baseline levels when the newly learned skills are fully consolidated.
#### **12.4.3 Altered Oscillations in Movement Disorders**
Given the contributions of beta oscillations in facilitating and inhibiting movements, it comes as no surprise that this rhythm may deviate in patients with movement disorders. This is most evident in Parkinson's disease, a neurodegenerative disorder where a loss of dopaminergic cells in substantia nigra may be accompanied by symptoms of rigidity (muscle stiffness), bradykinesia (slowness of movement), tremor, posture and balance problems, slurred speech, and several non-motor symptoms. The disease is initially treated with dopaminergic medication, but in a more advanced stage patients might be referred to DBS. Electrodes with multiple contacts are typically implanted in either STN or GPi in both left and right hemispheres. Both targets are known for the effect of 130-Hz stimulation on improvement of motor function (Deuschl et al., 2006; 272 Bernadette C. M. van Wijk
Weaver et al., 2009). Besides stimulation, the electrodes can be used to record LFPs, though recordings are typically limited to a time window of about a week after electrode implantation when wires are still externalized. Such recordings have revealed elevated levels of beta oscillations in patients off medication during rest (Figure 12.4; e.g., Brown et al., 2001; Levy et al., 2002; Priori et al., 2004), and some studies report lesspronounced beta ERD during self-paced movement (Doyle et al., 2005a).
One of the challenges with invasive recordings in patients is to determine the degree to which observed activities are physiological or disease-related. Acquiring the same recordings from healthy subjects for comparison is not an option as they would need to undergo the same surgical procedures. Still there are strong reasons to believe that excessive beta oscillations in the STN are a marker of Parkinsonism:
- 1. The amplitude of beta oscillations correlates with severity of bradykinesia and rigidity as measured with the Unified Parkinson's Disease Rating Scale (Neumann et al., 2016; van Wijk et al., 2016).
- 2. The amplitude of beta oscillations decreases after dopaminergic medication or DBS in parallel with clinical improvement (Kühn et al., 2009, 2008, 2006b; Ray et al., 2008).
- 3. The amplitude of beta oscillations in STN and GPi is higher in patients with Parkinson's disease than in patients with dystonia (Piña-Fuentes et al., 2019).
- 4. Stimulation at 20 Hz instead of the clinically effective 130 Hz impedes motor performance (Chen et al., 2007), therefore underscoring a causal role of excessive beta oscillations in motor impairment.
While bradykinesia and rigidity are associated with beta oscillations, tremor typically manifests at frequencies below 12 Hz. Several forms of physiological and pathological tremors with central or peripheral origins can be distinguished, all characterized by involuntary rhythmic movements in one or more body parts (Deuschl et al., 2001; McAuley & Marsden, 2000). Essential tremor is the most common movement disorder,

**Figure 12.4** Abnormal subthalamic nucleus oscillatory activity in Parkinson's disease. Left: Spectral power in the beta frequency range is elevated when the patient is withdrawn from dopaminergic medication. Right: Phase-amplitude coupling (PAC) between beta and highfrequency oscillations is another marker of motor impairment.
Example of single subject DBS-LFP recordings taken from Van Wijk et al., 2016.
OSCILLATORY ACTIVITY IN SENSORIMOTOR FUNCTION 273
an action tremor that occurs with voluntary muscle contraction. Neural entrainment between inferior olive, cerebellum, thalamus, and motor cortex is believed to underlie its emergence (Raethjen and Deuschl, 2012). Activity at the tremor frequency within this network has been found to be coherent with EMG (Hellwig et al., 2001; Schnitzler et al., 2009). By contrast, Parkinsonian tremor presents during rest and may have its origin in the basal ganglia (Deuschl et al., 2001). Both Parkinsonian and essential tremor can be suppressed by 130-Hz DBS in the ventrolateral thalamus (Benabid et al., 1996). Stimulation at the tremor frequency could either enhance or reduce tremor amplitude, depending on the phase at which stimulation pulses are delivered (Cagnan et al., 2013).
Dystonia is another hyperkinetic movement disorder that can be associated with increased power for frequencies below the beta band in GPi (Chen et al., 2006; Liu et al., 2008; Sharott et al., 2008; Silberstein et al., 2003). This arguably reflects diminished and more irregular neuronal firing that is considered distinctive of the disorder (Hendrix & Vitek, 2012). Clinical symptoms include twisting movements and abnormal posture resulting from involuntary sustained and sometimes repetitive muscle contractions (Fahn, 1988). Also in dystonia symptoms might be suppressed via DBS but improvement may not become evident before several weeks or months of continuous stimulation (Vidailhet et al., 2005). Barow et al. (2014) showed that 4–12 Hz pallidal activity is reduced upon DBS with more immediate effects for phasic compared to tonic dystonia subtypes.
Elevated levels of oscillatory activity seem to be a common feature of a number of movement disorders. Effective treatments are frequently associated with a reduction of this activity although causal relations are often difficult to establish.
## **12.5 A dynamic view on frequency bands**
Until now, averaging of spectral power within frequency bands or across long time windows has been common practice in the field. Recently, dynamical properties of oscillations have received more attention. For example, beta oscillations are not present with constant amplitude but appear in short bursts of varying amplitude and duration (Feingold et al., 2015; Murthy and Fetz, 1996b). In Parkinson's disease, bursts with long duration occur more frequently in the STN of patients with larger clinical impairment and also have a higher amplitude than short bursts (Tinkhauser et al., 2017a). Dopaminergic medication significantly reduces the number of long bursts (Tinkhauser et al., 2017b). These new insights help to further constrain computational models, like that proposed by Sherman and colleagues (2016) for S1, which explore the synaptic mechanisms by which beta bursts emerge.
Another example is the notion that functions may arise from the interaction between frequency bands as opposed to individual frequency bands forming parallel communication channels. Using recordings from rat motor cortex, Igarashi et al. (2013) 274 Bernadette C. M. van Wijk
demonstrated gamma oscillations comprised of a slow and fast component that were both coupled with an ongoing theta rhythm. Slow gamma oscillations were pronounced when rats were holding on to a lever and were phase-locked to peaks of the theta oscillation, whereas fast gamma oscillations emerged around the time of pulling the lever and were phase-locked to a trough of the theta oscillation. These findings are reminiscent of *phase precession* in hippocampal cortex where firing of place cells in the gamma range is nested in the ongoing theta rhythm. With individual gamma cycles representing a particular location in space, these progressively shift forward to earlier phases of the theta cycle as the rat navigates towards that location (O'Keefe & Recce, 1993). The nesting of oscillations allows for the encoding of near and far locations, i.e. information that is not contained in the individual frequencies. On the other hand, cross-frequency coupling might also arise due to pathology. We have found the strength of phase-amplitude coupling between beta and HFOs in the STN to correlate with the severity of bradykinesia and rigidity symptoms in Parkinson's disease (Figure 12.4; van Wijk et al., 2016).
Cross-frequency coupling could also be indicative of non-sinusoidal waveforms as these would appear at higher frequencies in the spectrum (van Wijk, 2017). Cole et al. (2017) demonstrated that the waveform shape of beta oscillations could indeed explain beta-gamma phase-amplitude coupling patterns observed in M1 of Parkinson's patients (de Hemptinne et al., 2013). It is interesting that DBS reduces the asymmetry of the beta oscillation waveform (de Hemptinne et al., 2015) as it hints at less-synchronous synaptic input from the basal ganglia. A focus on the detailed time dynamics, cross-frequency coupling, and waveform shape of oscillations holds great promise to further unravel their role in sensorimotor function.
# **12.6 Cognitive aspects of sensorimotor function**
We move to interact with the external world in a meaningful way. Our actions depend on goals and intentions, which in turn depend on the context we are in. Cognition and motor control are highly intertwined. Several lines of research indeed suggest that sensorimotor regions contribute beyond the classical view on motor control.
First of all, (pre-)motor cortex is already activated during the process of action selection instead of merely being informed on the final outcome that needs to be executed (Cisek and Kalaska, 2005). Donner and colleagues (2009) demonstrated that lateralized beta suppression and gamma increase in motor cortex could predict on a single trial level which left/right choice participants were going to make during a perceptual detection task. Instructions to emphasize decision speed versus accuracy decrease prestimulus M1 beta levels, which might explain the upsurge of errors under speed stress (Pastötter et al., 2012; Steinemann et al., 2018). Pre-decision activation of the motor system is therefore likely to speed-up or even influence behavioral performance.
OSCILLATORY ACTIVITY IN SENSORIMOTOR FUNCTION 275
The ability to *inhibit* actions is seen as an important marker of cognitive control. Pro-active inhibition and reactive stopping of actions are often studied with go/no-go and stop-signal paradigms, respectively. Both are thought to rely on the "stopping network" of inferior frontal gyrus (IFG), pre-SMA, and STN (Aron, 2011). In IFG, trials with a stop signal induce an increase in beta power that is larger for successful vs. unsuccessful stop trials (Swann et al., 2009). In STN, task-related beta suppression is weaker for successful compared to unsuccessful stops (Kühn et al., 2004; Wessel et al., 2016). In turn, successful stops are also characterized by a weaker beta suppression in M1 compared to unsuccessful stops (Swann et al., 2009). More generally, fronto-basal ganglia circuits are considered to act as a brake to stop actions, resolve conflict, or process surprising events (Aron et al., 2016).
Execution of movements is not strictly necessary for the sensorimotor system to become active. Beta ERD can be observed in contralateral M1 and the STN when participants are merely imagining that they are making a movement albeit with lower magnitude compared to real movements (Kühn et al., 2006a; Pfurtscheller and Neuper, 1997; Schnitzler et al., 1997). Researchers have gratefully taken advantage of this phenomenon for the development of *brain computer interfaces* (Wolpaw et al., 2002). Even patients in an advanced stage of ALS have been able to learn how to control vertical cursor movement on a computer screen by up- or down-regulating the amplitude of sensorimotor EEG rhythms via motor imagery (Kübler et al., 2005). With the use of machine learning it is possible to reduce the training time needed to successfully operate such a device to just 20 minutes in healthy individuals (Blankertz et al., 2007). Controlling a robot arm or computer cursor by imagining movement of your own limb is appealing as it relies to a large extent on how the brain controls real movements.
Observing movements performed by others can also induce alpha/mu and beta suppression in human sensorimotor cortex (Babiloni et al., 2002; Cochin et al., 1998; Hari et al., 1998; Kilner et al., 2009). The suppression is slightly larger when the action is target-directed (Avanzini et al., 2012; Muthukumaraswamy et al., 2004) and when the observer is more experienced with the action him/herself (Cannon et al., 2014). A credible hypothesis for the activation of motor regions during perception is that the observed action needs to be internally simulated in order to understand the other person's actions and intentions (Jeannerod, 2001). As such, the discovery of *mirror neurons* in (pre-) motor regions (Cattaneo & Rizzolatti, 2009) means that considerable ground is shared with the field of social neuroscience.
## **12.7 Conclusions**
Oscillations are omnipresent in the sensorimotor system and show distinct modulations with experimental tasks and pathology. In particular beta oscillations seem to have a prominent role by means of their association with movement facilitation and inhibition. Movement-related beta ERD and ERS are among the most robust time-frequency 276 Bernadette C. M. van Wijk
patterns in EEG/MEG studies. Intriguingly, the cortex is not alone in displaying these characteristic modulations. Very similar movement-related beta ERD/ERS and gamma ERS can be observed in LFP recordings from the STN (Alegre et al., 2005; Androulidakis et al., 2007b; Cassidy et al., 2002; Kühn et al., 2004; Litvak et al., 2012), GPi (Brücke et al., 2008; Talakoub et al., 2016; Tsang et al., 2012), and the ventral lateral thalamus (Brücke et al., 2013; Klostermann et al., 2007; Paradiso et al., 2004). This implies that these modulations are generic principles of information processing that might have different functional meaning in different regions of the sensorimotor network.
Over the years, the main focus of the field at large has been on oscillations in contralateral M1. While simple flexion/extension movements of the fingers indeed seem to be fairly restricted to activation in the primary sensorimotor cortices, more complex rhythmic or bimanual movement patterns recruit additional regions like ipsilateral M1, SMA, premotor cortex, cerebellum, and also primary and secondary sensory and association cortices if the task involves strong visual or auditory components (Heinrichs-Graham & Wilson, 2015; Houweling et al., 2008; Hummel et al., 2003; Pollok et al., 2005; Rueda-Delgado et al., 2014). The contribution of subcortical structures is more difficult to study in humans but should not be overlooked. Intriguingly, lesions to motor cortex do not affect execution of a task-specific motor sequence in rats once the sequence has been learned, suggesting reliance on subcortical controllers with projections to the spinal cord (Kawai et al., 2015). Simultaneous MEG and DBS-LFP recordings have revealed a number of spatially and spectrally distinct cortico-subcortical networks that appear to be disease-unrelated. The functional relevance of these networks deserves further exploration in future studies.
Although we have learned a great deal about the neural control of movement by studying oscillations, several aspects remain unexplained. Important questions that are still open are mostly of mechanistic nature. For example, how does beta ERD lead to muscle activations? What causes beta ERD to start and initiate movement in the first place? Why is desynchronization so widespread even for simple finger movement? Why are movement-related modulations so similar across various parts of the motor system? How are movement plans translated into motor commands? How are they encoded? Oscillations reflect the summed activity of numerous neurons, from which it might be difficult to infer details of individual muscle control especially with noninvasive techniques such as EEG and MEG. Instead, they are more likely to reflect general states of activation or deactivation. I believe there is still much more to gain from studying oscillations through the combination of recordings techniques, the use of advanced signal processing algorithms and the development of computational models. Fortunately, grasping a cup of coffee is much easier than understanding how we do it.
#### **REFERENCES**
Adrian, E. D. & Matthews, B. H. C. (1934). The Berger rhythm: Potential changes from the occipital lobes in man. *Brain*, *57*, 355–385.
OSCILLATORY ACTIVITY IN SENSORIMOTOR FUNCTION 277
- Alayrangues, J., Torrecillos, F., Jahani, A., & Malfait, N. (2019). Error-related modulations of the sensorimotor post-movement and foreperiod beta-band activities arise from distinct neural substrates and do not reflect efferent signal processing. *NeuroImage 184*, 10–24.
- Alegre, M., Alonso-Frech, F., Rodríguez-Oroz, M. C., Guridi, J., Zamarbide, I., Valencia, M., . . . Artieda, J. (2005). Movement-related changes in oscillatory activity in the human subthalamic nucleus: Ipsilateral vs. contralateral movements. *European Journal of Neuroscience*, *22*, 2315–2324.
- Alegre, M., Labarga, A., Gurtubay, I., Iriarte, J., Malanda, A., & Artieda, J. (2003). Movementrelated changes in cortical oscillatory activity in ballistic, sustained and negative movements. *Experimental Brain Research*, *148*, 17–25.
- Andres, F. G., Mima, T., Schulman, A. E., Dichgans, J., Hallett, M., & Gerloff, C. (1999). Functional coupling of human cortical sensorimotor areas during bimanual skill acquisition. *Brain*, *122*, 855–870.
- Androulidakis, A. G., Doyle, L. M. F., Yarrow, K., Litvak, V., Gilbertson, T. P., & Brown, P. (2007a). Anticipatory changes in beta synchrony in the human corticospinal system and associated improvements in task performance. *European Journal of Neuroscience*, *25*, 3758– 3765.
- Androulidakis, A. G., Kühn, A. A., Chen, C. C., Blomstedt, P., Kempf, F., Kupsch, A., . . . Brown, P. (2007b). Dopaminergic therapy promotes lateralized motor activity in the subthalamic area in Parkinson's disease. *Brain*, *130*, 457–68.
- Aron, A. R. (2011). From reactive to proactive and selective control: Developing a richer model for stopping inappropriate responses. *Biological Psychiatry*, *69*, e55–e68. [https://doi.org/](https://doi.org/10.1016/j.biopsych.2010.07.024) [10.1016/j.biopsych.2010.07.024](https://doi.org/10.1016/j.biopsych.2010.07.024)
- Aron, A. R., Herz, D. M., Brown, P., Forstmann, B. U., & Zaghloul, K. (2016). Frontosubthalamic circuits for control of action and cognition. *Journal of Neuroscience*, *36*, 11489–11495. [https://](https://doi.org/10.1523/JNEUROSCI.2348-16.2016) [doi.org/10.1523/JNEUROSCI.2348-16.2016](https://doi.org/10.1523/JNEUROSCI.2348-16.2016)
- Asanuma, H., Zarzecki, P., Jankowska, E., Hongo, T., & Marcus, S. (1979). Projection of individual pyramidal tract neurons to lumbar motor nuclei of the monkey. *Experimental Brain Research*, *34*, 73–89.
- Ashe, J. & Georgopoulos, A. P. (1994). Movement parameters and neural activity in motor cortex and area 5. *Cerebral Cortex*, *4*, 590–600.
- Avanzini, P., Fabbri-Destro, M., Dalla Volta, R., Daprati, E., Rizzolatti, G., & Cantalupo, G. (2012). The dynamics of sensorimotor cortical oscillations during the observation of hand movements: An EEG study. *PLoS One*, *7*, e37534. [https://doi.org/10.1371/journal.](https://doi.org/10.1371/journal.pone.0037534) [pone.0037534](https://doi.org/10.1371/journal.pone.0037534)
- Babiloni, C., Babiloni, F., Carducci, F., Cincotti, F., Cocozza, G., Del Percio, C., Moretti, D. V., & Rossini, P. M. (2002). Human cortical electroencephalography (EEG) rhythms during the observation of simple aimless movements: A high-resolution EEG study. *NeuroImage*, *17*, 559–572.
- Baker, M. R. & Baker, S. N. (2003). The effect of diazepam on motor cortical oscillations and corticomuscular coherence studied in man. *Journal of Physiology, 546*, 931–942. [https://doi.](https://doi.org/10.1113/jphysiol.2002.029553) [org/10.1113/jphysiol.2002.029553](https://doi.org/10.1113/jphysiol.2002.029553)
- Baker, S. N., Olivier, E., & Lemon, R. N. (1997). Coherent oscillations in monkey motor cortex and hand muscle EMG show task-dependent modulation. *Journal of Physiology*, *501*, 225– 241.
278 Bernadette C. M. van Wijk
- Baker, S. N., Pinches, E. M., & Lemon, R. N. (2003). Synchronization in monkey motor cortex during a precision grip task. II. Effect of oscillatory activity on corticospinal output. *Journal of Neurophysiology*, *89*, 1941–1953.
- Baker, S. N., Spinks, R., Jackson, A., & Lemon, R. N. (2001). Synchronization in monkey motor cortex during a precision grip task. I. Task-dependent modulation in single-unit synchrony. *Journal of Neurophysiology*, *85*, 869–885.
- Barow, E., Neumann, W. J., Brücke, C., Huebl, J., Horn, A., Brown, P., . . . Kühn, A.A., 2014. Deep brain stimulation suppresses pallidal low frequency activity in patients with phasic dystonic movements. *Brain*, *137*, 3012–3024.
- Benabid, A. L., Pollak, P., Gao, D., Hoffmann, D., Limousin, P., Gay, E., Payen, I., & Benazzouz, A. (1996). Chronic electrical stimulation of the ventralis intermedius nucleus of the thalamus as a treatment of movement disorders. *Journal of Neurosurgery*, *84*, 203–214. [https://](https://doi.org/10.3171/jns.1996.84.2.0203) [doi.org/10.3171/jns.1996.84.2.0203](https://doi.org/10.3171/jns.1996.84.2.0203)
- Berger, H. (1929). Über das Elektroenkephalogramm des Menschen. *Archiv für Psychiatrie und Nervenkrankheiten*, *87*, 527–570.
- Bhatt, M. B., Bowen, S., Rossiter, H. E., Dupont-Hadwen, J., Moran, R.J., Friston, K.J., Ward, N.S., 2016. Computational modelling of movement-related beta-oscillatory dynamics in human motor cortex. *Neuroimage 133*, 224–232. [https://doi.org/10.1016/j.neuroim](https://doi.org/10.1016/j.neuroimage.2016.02.078) [age.2016.02.078](https://doi.org/10.1016/j.neuroimage.2016.02.078)
- Blankertz, B., Dornhege, G., Krauledat, M., Müller, K.-R., & Curio, G. (2007). The non-invasive Berlin Brain–Computer Interface: Fast acquisition of effective performance in untrained subjects. *NeuroImage*, *37*, 539–550.
- Boonstra, T. W., Daffertshofer, A., Breakspear, M., & Beek, P. J. (2007). Multivariate time– frequency analysis of electromagnetic brain activity during bimanual motor learning. *NeuroImage*, *36*, 370–377.
- Boonstra, T. W., Danna-Dos-Santos, A., Xie, H.-B., Roerdink, M., Stins, J. F., & Breakspear, M. (2016). Muscle networks: Connectivity analysis of EMG activity during postural control. *Scientific Reports*, *5*, 17830.
- Boonstra, T. W., van Wijk, B. C. M., Praamstra, P., & Daffertshofer, A. (2009). Corticomuscular and bilateral EMG coherence reflect distinct aspects of neural synchronization. *Neuroscience Letters*, *463*, 17–21.
- Brown, P., Oliviero, A., Mazzone, P., Insola, A., Tonali, P., & Di Lazzaro, V. (2001). Dopamine dependency of oscillations between subthalamic nucleus and pallidum in Parkinson's disease. *Journal of Neuroscience*, *21*, 1033–1038. [https://doi.org/10.1523/JNEURO](https://doi.org/10.1523/JNEUROSCI.21-03-01033.2001) [SCI.21-03-01033.2001](https://doi.org/10.1523/JNEUROSCI.21-03-01033.2001)
- Brown, P., Salenius, S., Rothwell, J. C., & Hari, R. (1998). Cortical correlate of the Piper rhythm in humans. *Journal of Neurophysiology*, *80*, 2911–2917. [https://doi.org/10.1152/](https://doi.org/10.1152/jn.1998.80.6.2911) [jn.1998.80.6.2911](https://doi.org/10.1152/jn.1998.80.6.2911)
- Brücke, C., Bock, A., Huebl, J., Krauss, J. K., Schönecker, T., Schneider, G. H., Brown, P., & Kühn, A. A. (2013). Thalamic gamma oscillations correlate with reaction time in a go/no-go task in patients with essential tremor. *NeuroImage*, *75*, 36–45. [https://doi.org/10.1016/j.neu](https://doi.org/10.1016/j.neuroimage.2013.02.038) [roimage.2013.02.038](https://doi.org/10.1016/j.neuroimage.2013.02.038)
- Brücke, C., Kempf, F., Kupsch, A., Schneider, G. H., Krauss, J.K., Aziz, T., . . . Kühn, A. A. (2008). Movement-related synchronization of gamma activity is lateralized in patients with dystonia. *European Journal of Neuroscience*, *27*, 2322–2329. [https://doi.org/10.1111/](https://doi.org/10.1111/j.1460-9568.2008.06203.x) [j.1460-9568.2008.06203.x](https://doi.org/10.1111/j.1460-9568.2008.06203.x)
OSCILLATORY ACTIVITY IN SENSORIMOTOR FUNCTION 279
- Cagnan, H., Brittain, J.-S., Little, S., Foltynie, T., Limousin, P., Zrinzo, L., . . . Brown, P. (2013). Phase dependent modulation of tremor amplitude in essential tremor through thalamic stimulation. *Brain*, *136*, 3062–3075.
- Cannon, E. N., Yoo, K. H., Vanderwert, R. E., Ferrari, P. F., Woodward, A.L., & Fox, N. A. (2014). Action experience, more than observation, influences mu rhythm desynchronization. *PLoS One*, *9*, e92002.
- Cardoso de Oliveira, S., Gribova, A., Donchin, O., Bergman, H., & Vaadia, E. (2001). Neural interactions between motor cortical hemispheres during bimanual and unimanual arm movements. *European Journal of Neuroscience*, *14*, 1881–1896. [https://doi.org/10.1046/](https://doi.org/10.1046/j.0953-816X.2001.01801.x) [j.0953-816X.2001.01801.x](https://doi.org/10.1046/j.0953-816X.2001.01801.x)
- Cassidy, M., Mazzone, P., Oliviero, A., Insola, A., Tonali, P., Di Lazzaro, V., & Brown, P. (2002). Movement-related changes in synchronization in the human basal ganglia. *Brain*, *125*, 1235– 1246.
- Cassim, F., Monaca, C., Szurhaj, W., Bourriez, J.-L., Defebvre, L., Derambure, P., & Guieu, J.-D. (2001). Does post-movement beta synchronization reflect an idling motor cortex? *Neuroreport*, *12*, 3859–3863.
- Cassim, F., Szurhaj, W., Sediri, H., Devos, D., Bourriez, J.-L., Poirot, I., . . . Guieu, J.-D. (2000). Brief and sustained movements: Differences in event-related (de)synchronization (ERD/ERS) patterns. *Clinical Neurophysiology*, *111*, 2032–2039. [https://doi.org/10.1016/](https://doi.org/10.1016/S1388-2457(00)00455-7) [S1388-2457\(00\)00455-7](https://doi.org/10.1016/S1388-2457(00)00455-7)
- Cattaneo, L. & Rizzolatti, G. (2009). The mirror neuron system. *Archives of Neurology*, *66*, 557– 560.
- Chakarov, V., Naranjo, J.R., Schulte-Monting, J., Omlor, W., Huethe, F., & Kristeva, R. (2009). Beta-range EEG-EMG coherence with isometric compensation for increasing modulated lowlevel forces. *Journal of Neurophysiology*, *102*, 1115–1120.
- Chatrian, G. E., Petersen, M. C., & Lazarte, J. A. (1959). The blocking of the Rolandic wicket rhythm and some central changes related to movement. *Electroencephalography and Clinical Neurophysiology*, *11*, 497–510. [https://doi.org/10.1016/0013-4694\(59\)90048-3](https://doi.org/10.1016/0013-4694(59)90048-3)
- Chen, C.C., Kühn, A.A., Hoffmann, K.T., Kupsch, A., Schneider, G.H., Trottenberg, T., . . . Brown, P. (2006). Oscillatory pallidal local field potential activity correlates with involuntary EMG in dystonia. *Neurology*, *66*, 418–420. [https://doi.org/10.1212/01.wnl.0000196](https://doi.org/10.1212/01.wnl.0000196470.00165.7d) [470.00165.7d](https://doi.org/10.1212/01.wnl.0000196470.00165.7d)
- Chen, C. C., Litvak, V., Gilbertson, T., Kühn, A., Lu, C., Lee, S., . . . Hariz, M. (2007). Excessive synchronization of basal ganglia neurons at 20 Hz slows movement in Parkinson's disease. *Experimental Neurology*, *205*, 214–221.
- Chen, R., Yaseen, Z., Cohen, L. G., & Hallett, M. (1998). Time course of corticospinal excitability in reaction time and self-paced movements. *Annals of Neurology*, *44*, 317–325. [https://](https://doi.org/10.1002/ana.410440306) [doi.org/10.1002/ana.410440306](https://doi.org/10.1002/ana.410440306)
- Cheyne, D., Bells, S., Ferrari, P., Gaetz, W., & Bostan, A. C. (2008). Self-paced movements induce high-frequency gamma oscillations in primary motor cortex. *NeuroImage*, *42*, 332–342.
- Cheyne, D., Gaetz, W., Garnero, L., Lachaux, J.-P., Ducorps, A., Schwartz, D., & Varela, F. J. (2003). Neuromagnetic imaging of cortical oscillations accompanying tactile stimulation. *Cognitive Brain Research*, *17*, 599–611. [https://doi.org/10.1016/S0926-6410\(03\)00173-3](https://doi.org/10.1016/S0926-6410(03)00173-3)
- Cisek, P. & Kalaska, J. F. (2005). Neural correlates of reaching decisions in dorsal premotor cortex: specification of multiple direction choices and final selection of action. *Neuron*, *45*, 801–814.
280 Bernadette C. M. van Wijk
- Classen, J., Gerloff, C., Honda, M., & Hallett, M. (1998) Integrative visuomotor behavior is associated with interregionally coherent oscillations in the human brain. *Journal of Neurophysiology*, *79*, 1567–1573.
- Cochin, S., Barthelemy, C., Lejeune, B., Roux, S., & Martineau, J. (1998). Perception of motion and qEEG activity in human adults. *Electroencephalography and Clinical Neurophysiology*, *107*, 287–295. [https://doi.org/10.1016/S0013-4694\(98\)00071-6](https://doi.org/10.1016/S0013-4694(98)00071-6)
- Cole, S. R., van der Meij, R., Peterson, E. J., de Hemptinne, C., Starr, P. A., & Voytek, B. (2017). Nonsinusoidal beta oscillations reflect cortical pathophysiology in Parkinson's disease. *Journal of Neuroscience*, *37*, 2208–2216.
- Conway, B. A., Halliday, D. M., Farmer, S. F., Shahani, U., Maas, P., Weir, A. I., & Rosenberg, J. R. (1995). Synchronization between motor cortex and spinal motoneuronal pool during the performance of a maintained motor task in man. *Journal of Physiology*, *489*, 917–924. [https://](https://doi.org/10.1113/jphysiol.1995.sp021104) [doi.org/10.1113/jphysiol.1995.sp021104](https://doi.org/10.1113/jphysiol.1995.sp021104)
- Crone, N. E., Miglioretti, D. L., Gordon, B., & Lesser, R. P. (1998a). Functional mapping of human sensorimotor cortex with electrocorticographic spectral analysis. II. Event-related synchronization in the gamma band. *Brain*, *121*, 2301–2315. [https://doi.org/10.1093/brain/](https://doi.org/10.1093/brain/121.12.2301) [121.12.2301](https://doi.org/10.1093/brain/121.12.2301)
- Crone, N. E., Miglioretti, D. L., Gordon, B., Sieracki, J. M., Wilson, M. T., Uematsu, S., & Lesser, R. P. (1998b). Functional mapping of human sensorimotor cortex with electrocorticographic spectral analysis. I. Alpha and beta event-related desynchronization. *Brain*, *121*, 2271–2299.
- de Hemptinne, C., Ryapolova-Webb, E. S., Air, E. L., Garcia, P. A., Miller, K. J., Ojemann, J. G.,. . . Starr, P. A. (2013). Exaggerated phase-amplitude coupling in the primary motor cortex in Parkinson disease. *Proceedings of the National Academy of Sciences of the United States of America*, *110*, 4780–4785.
- de Hemptinne, C., Swann, N. C., Ostrem, J. L., Ryapolova-Webb, E. S., San Luciano, M., Galifianakis, N. B., & Starr, P. A. (2015). Therapeutic deep brain stimulation reduces cortical phase-amplitude coupling in Parkinson's disease. *Nature Neuroscience*, *18*, 779–786. [https://](https://doi.org/10.1038/nn.3997) [doi.org/10.1038/nn.3997](https://doi.org/10.1038/nn.3997)
- Denker, M., Roux, S., Timme, M., Riehle, A., & Grün, S. (2007). Phase synchronization between LFP and spiking activity in motor cortex during movement preparation. *Neurocomputing*, *70*, 2096–2101.
- Deuschl, G., Raethjen, J., Lindemann, M., & Krack, P. (2001). The pathophysiology of tremor. *Muscle Nerve*, *24*, 716–735.
- Deuschl, G., Schade-Brittinger, C., Krack, P., Volkmann, J., Schäfer, H., Bötzel, K., . . . Voges, J. (2006). A randomized trial of deep-brain stimulation for Parkinson's disease. *New England Journal of Medicine*, *355*, 896–908.
- Donner, T. H., Siegel, M., Fries, P., & Engel, A. K. (2009). Buildup of choice-predictive activity in human motor cortex during perceptual decision making. *Current Biology*, *19*, 1581–1585.
- Doyle, L. M. F., Kühn, A. A., Hariz, M., Kupsch, A., Schneider, G. H., & Brown, P. (2005a). Levodopa-induced modulation of subthalamic beta oscillations during self-paced movements in patients with Parkinson's disease. *European Journal of Neuroscience*,. *21*, 1403– 1412.
- Doyle, L. M. F., Yarrow, K., & Brown, P. (2005b). Lateralization of event-related beta desynchronization in the EEG during pre-cued reaction time tasks. *Clinical Neurophysiology*, *116*, 1879–1888.
OSCILLATORY ACTIVITY IN SENSORIMOTOR FUNCTION 281
- Erbil, N. & Ungan, P. (2007). Changes in the alpha and beta amplitudes of the central EEG during the onset, continuation, and offset of long-duration repetitive hand movements. *Brain Research*, *1169*, 44–56.
- Espenhahn, S., de Berker, A. O., van Wijk, B. C. M., Rossiter, H. E., & Ward, N. S. (2017). Movement-related beta oscillations show high intra-individual reliability. *NeuroImage*, *147*, 175–185.
- Espenhahn, S., van Wijk, B. C. M., Rossiter, H. E., de Berker, A. O., Redman, N. D., Rondina, J., Diedrichsen, J., & Ward, N. S. (2019). Cortical beta oscillations are associated with motor performance following visuomotor learning. *NeuroImage*, *195*, 340–353. [https://doi.org/](https://doi.org/10.1016/j.neuroimage.2019.03.079) [10.1016/j.neuroimage.2019.03.079](https://doi.org/10.1016/j.neuroimage.2019.03.079)
- Fahn, S. (1988). Concept and classification of dystonia. *Advances in Neurology*, *50*, 1–8.
- Feingold, J., Gibson, D. J., DePasquale, B., & Graybiel, A. M. (2015). Bursts of beta oscillation differentiate postperformance activity in the striatum and motor cortex of monkeys performing movement tasks. *Proceedings of the National Academy of Sciences of the United States of America*, *112*, 13687–92.
- Foffani, G., Priori, A., Egidi, M., Rampini, P., Tamma, F., Caputo, E., . . . Barbieri, S. (2003). 300- Hz subthalamic oscillations in Parkinson's disease. *Brain*, *126*, 2153–2163. [https://doi.org/](https://doi.org/10.1093/brain/awg229) [10.1093/brain/awg229](https://doi.org/10.1093/brain/awg229)
- Freund, H. J. (1983). Motor unit and muscle activity in voluntary motor control. *Physiological Reviews*, *63*, 387–436.
- Fries, P. (2005). A mechanism for cognitive dynamics: Neuronal communication through neuronal coherence. *Trends in Cognitive Science*, *9*, 474–480. [https://doi.org/10.1016/](https://doi.org/10.1016/j.tics.2005.08.011) [j.tics.2005.08.011](https://doi.org/10.1016/j.tics.2005.08.011)
- Fu, Q. G., Flament, D., Coltz, J. D., & Ebner, T. J. (1995). Temporal encoding of movement kinematics in the discharge of primate primary motor and premotor neurons. *Journal of Neurophysiology*, *73*, 836–854.
- Gaetz, W., MacDonald, M., Cheyne, D., & Snead, O. C. (2010). Neuromagnetic imaging of movement-related cortical oscillations in children and adults: Age predicts post-movement beta rebound. *NeuroImage*, *51*, 792–807.
- Gastaut, H. (1952). Etude électrocorticographique de la réactivité des rythmes rolandiques. *Revue neurologique*, *87*, 176–82.
- Georgopoulos, A., Schwartz, A., & Kettner, R. (1986). Neuronal population coding of movement direction. *Science*, *233*, 1416–1419.
- Gerloff, C., Richard, J., Hadley, J., Schulman, A.E., Honda, M., Hallett, M., 1998. Functional coupling and regional activation of human cortical motor areas during simple, internally paced and externally paced finger movements. *Brain 121*, 1513–1531. [https://doi.org/10.1093/](https://doi.org/10.1093/brain/121.8.1513) [brain/121.8.1513](https://doi.org/10.1093/brain/121.8.1513)
- Gilbertson, T., Lalo, E., Doyle, L., Lazzaro, V. Di, Cioni, B., & Brown, P. (2005). Existing motor state is favored at the expense of new movement during 13–35 Hz oscillatory synchrony in the human corticospinal system. *Journal of Neuroscience*, *25*, 7771–7779. [https://doi.org/](https://doi.org/10.1523/JNEUROSCI.1762-05.2005) [10.1523/JNEUROSCI.1762-05.2005](https://doi.org/10.1523/JNEUROSCI.1762-05.2005)
- Grammont, F. & Riehle, A. (2003). Spike synchronization and firing rate in a population of motor cortical neurons in relation to movement direction and reaction time. *Biological Cybernetics*, *88*, 360–373.
- Gross, J., Pollok, B., Dirks, M., Timmermann, L., Butz, M., & Schnitzler, A. (2005). Taskdependent oscillations during unimanual and bimanual movements in the human primary
282 Bernadette C. M. van Wijk
- motor cortex and SMA studied with magnetoencephalography. *NeuroImage*, *26*, 91–98.
- Gross, J., Tass, P. A., Salenius, S., Hari, R., Freund, H. J., & Schnitzler, A. (2000). Corticomuscular synchronization during isometric muscle contraction in humans as revealed by magnetoencephalography. *Journal of Physiology*, *527*, 623–631. [https://doi.org/10.1111/](https://doi.org/10.1111/j.1469-7793.2000.00623.x) [j.1469-7793.2000.00623.x](https://doi.org/10.1111/j.1469-7793.2000.00623.x)
- Hall, S. D., Barnes, G. R., Furlong, P. L., Seri, S., & Hillebrand, A. (2010). Neuronal network pharmacodynamics of GABAergic modulation in the human cortex determined using pharmaco-magnetoencephalography. *Human Brain Mapping*, *31*, 581–594. [https://doi.org/](https://doi.org/10.1002/hbm.20889) [10.1002/hbm.20889](https://doi.org/10.1002/hbm.20889)
- Halliday, D. M., Conway, B. A., Farmer, S. F., and Rosenberg, J. R. (1998). Using electroencephalography to study functional coupling between cortical activity and electromyograms during voluntary contractions in humans. *Neuroscience Letters*, *241*, 5–8. [https://doi.org/](https://doi.org/10.1016/S0304-3940(97)00964-6) [10.1016/S0304-3940\(97\)00964-6](https://doi.org/10.1016/S0304-3940(97)00964-6)
- Hari, R., Forss, N., Avikainen, S., Kirveskari, E., Salenius, S., & Rizzolatti, G. (1998). Activation of human primary motor cortex during action observation: A neuromagnetic study. *Proceedings of the National Academy of Sciences of the United States of America*, *95*, 15061– 15065.
- Heinrichs-Graham, E., McDermott, T. J., Mills, M. S., Wiesman, A. I., Wang, Y.-P., Stephen, J. M., Calhoun, V. D., & Wilson, T. W. (2018). The lifespan trajectory of neural oscillatory activity in the motor system. *Developmental Cognitive Neuroscience*, *30*, 159–168. [https://doi.](https://doi.org/10.1016/j.dcn.2018.02.013) [org/10.1016/j.dcn.2018.02.013](https://doi.org/10.1016/j.dcn.2018.02.013)
- Heinrichs-Graham, E. & Wilson, T. W. (2015). Coding complexity in the human motor circuit. *Human Brain Mapping*, *36*, 5155–5167.
- Hellwig, B., Häußler, S., Schelter, B., Lauk, M., Guschlbauer, B., Timmer, J., & Lücking, C. H. (2001). Tremor-correlated cortical activity in essential tremor. *The Lancet*, *357*, 519–523. [https://doi.org/10.1016/S0140-6736\(00\)04044-7](https://doi.org/10.1016/S0140-6736(00)04044-7)
- Hendrix, C. M. & Vitek, J. L. (2012). Toward a network model of dystonia. *Annals of the New York Academy of Sciences*, *1265*, 46–55. [https://doi.org/10.1111/](https://doi.org/10.1111/j.1749-6632.2012.06692.x) [j.1749-6632.2012.06692.x](https://doi.org/10.1111/j.1749-6632.2012.06692.x)
- Hillebrand, A., Barnes, G. R., Bosboom, J. L., Berendse, H. W., & Stam, C. J. (2012). Frequencydependent functional connectivity within resting-state networks: An atlas-based MEG beamformer solution. *NeuroImage*, *59*, 3909–3921. [https://doi.org/10.1016/j.neuroim](https://doi.org/10.1016/j.neuroimage.2011.11.005) [age.2011.11.005](https://doi.org/10.1016/j.neuroimage.2011.11.005)
- Hirschmann, J., Butz, M., Hartmann, C. J., Hoogenboom, N., Özkurt, T. E., Vesper, J., Wojtecki, L., & Schnitzler, A. (2016). Parkinsonian rest tremor is associated with modulations of subthalamic high-frequency oscillations. *Movement Disorders*, *31*, 1551–1559. [https://doi.org/](https://doi.org/10.1002/mds.26663) [10.1002/mds.26663](https://doi.org/10.1002/mds.26663)
- Hirschmann, J., Özkurt, T. E., Butz, M., Homburger, M., Elben, S., Hartmann, C. J., . . . Schnitzler, A. (2011). Distinct oscillatory STN-cortical loops revealed by simultaneous MEG and local field potential recordings in patients with Parkinson's disease. *NeuroImage*, *55*, 1159–1168.
- Hirschmann, J., Özkurt, T.E., Butz, M., Homburger, M., Elben, S., Hartmann, C.J., . . . Schnitzler, A. (2013). Differential modulation of STN-cortical and cortico-muscular coherence by movement and levodopa in Parkinson's disease. *NeuroImage*, *68*, 203–213. [https://doi.org/](https://doi.org/10.1016/j.neuroimage.2012.11.036) [10.1016/j.neuroimage.2012.11.036](https://doi.org/10.1016/j.neuroimage.2012.11.036)282 Bernadette C. M. van Wijk
- motor cortex and SMA studied with magnetoencephalography. *NeuroImage*, *26*, 91–98.
- Gross, J., Tass, P. A., Salenius, S., Hari, R., Freund, H. J., & Schnitzler, A. (2000). Corticomuscular synchronization during isometric muscle contraction in humans as revealed by magnetoencephalography. *Journal of Physiology*, *527*, 623–631. [https://doi.org/10.1111/](https://doi.org/10.1111/j.1469-7793.2000.00623.x) [j.1469-7793.2000.00623.x](https://doi.org/10.1111/j.1469-7793.2000.00623.x)
- Hall, S. D., Barnes, G. R., Furlong, P. L., Seri, S., & Hillebrand, A. (2010). Neuronal network pharmacodynamics of GABAergic modulation in the human cortex determined using pharmaco-magnetoencephalography. *Human Brain Mapping*, *31*, 581–594. [https://doi.org/](https://doi.org/10.1002/hbm.20889) [10.1002/hbm.20889](https://doi.org/10.1002/hbm.20889)
- Halliday, D. M., Conway, B. A., Farmer, S. F., and Rosenberg, J. R. (1998). Using electroencephalography to study functional coupling between cortical activity and electromyograms during voluntary contractions in humans. *Neuroscience Letters*, *241*, 5–8. [https://doi.org/](https://doi.org/10.1016/S0304-3940(97)00964-6) [10.1016/S0304-3940\(97\)00964-6](https://doi.org/10.1016/S0304-3940(97)00964-6)
- Hari, R., Forss, N., Avikainen, S., Kirveskari, E., Salenius, S., & Rizzolatti, G. (1998). Activation of human primary motor cortex during action observation: A neuromagnetic study. *Proceedings of the National Academy of Sciences of the United States of America*, *95*, 15061– 15065.
- Heinrichs-Graham, E., McDermott, T. J., Mills, M. S., Wiesman, A. I., Wang, Y.-P., Stephen, J. M., Calhoun, V. D., & Wilson, T. W. (2018). The lifespan trajectory of neural oscillatory activity in the motor system. *Developmental Cognitive Neuroscience*, *30*, 159–168. [https://doi.](https://doi.org/10.1016/j.dcn.2018.02.013) [org/10.1016/j.dcn.2018.02.013](https://doi.org/10.1016/j.dcn.2018.02.013)
- Heinrichs-Graham, E. & Wilson, T. W. (2015). Coding complexity in the human motor circuit. *Human Brain Mapping*, *36*, 5155–5167.
- Hellwig, B., Häußler, S., Schelter, B., Lauk, M., Guschlbauer, B., Timmer, J., & Lücking, C. H. (2001). Tremor-correlated cortical activity in essential tremor. *The Lancet*, *357*, 519–523. [https://doi.org/10.1016/S0140-6736\(00\)04044-7](https://doi.org/10.1016/S0140-6736(00)04044-7)
- Hendrix, C. M. & Vitek, J. L. (2012). Toward a network model of dystonia. *Annals of the New York Academy of Sciences*, *1265*, 46–55. [https://doi.org/10.1111/](https://doi.org/10.1111/j.1749-6632.2012.06692.x) [j.1749-6632.2012.06692.x](https://doi.org/10.1111/j.1749-6632.2012.06692.x)
- Hillebrand, A., Barnes, G. R., Bosboom, J. L., Berendse, H. W., & Stam, C. J. (2012). Frequencydependent functional connectivity within resting-state networks: An atlas-based MEG beamformer solution. *NeuroImage*, *59*, 3909–3921. [https://doi.org/10.1016/j.neuroim](https://doi.org/10.1016/j.neuroimage.2011.11.005) [age.2011.11.005](https://doi.org/10.1016/j.neuroimage.2011.11.005)
- Hirschmann, J., Butz, M., Hartmann, C. J., Hoogenboom, N., Özkurt, T. E., Vesper, J., Wojtecki, L., & Schnitzler, A. (2016). Parkinsonian rest tremor is associated with modulations of subthalamic high-frequency oscillations. *Movement Disorders*, *31*, 1551–1559. [https://doi.org/](https://doi.org/10.1002/mds.26663) [10.1002/mds.26663](https://doi.org/10.1002/mds.26663)
- Hirschmann, J., Özkurt, T. E., Butz, M., Homburger, M., Elben, S., Hartmann, C. J., . . . Schnitzler, A. (2011). Distinct oscillatory STN-cortical loops revealed by simultaneous MEG and local field potential recordings in patients with Parkinson's disease. *NeuroImage*, *55*, 1159–1168.
- Hirschmann, J., Özkurt, T.E., Butz, M., Homburger, M., Elben, S., Hartmann, C.J., . . . Schnitzler, A. (2013). Differential modulation of STN-cortical and cortico-muscular coherence by movement and levodopa in Parkinson's disease. *NeuroImage*, *68*, 203–213. [https://doi.org/](https://doi.org/10.1016/j.neuroimage.2012.11.036) [10.1016/j.neuroimage.2012.11.036](https://doi.org/10.1016/j.neuroimage.2012.11.036)
OSCILLATORY ACTIVITY IN SENSORIMOTOR FUNCTION 283
- Houweling, S., Daffertshofer, A., van Dijk, B. W., & Beek, P. J. (2008). Neural changes induced by learning a challenging perceptual-motor task. *NeuroImage*, *41*, 1395–1407. [https://doi.org/](https://doi.org/10.1016/j.neuroimage.2008.03.023) [10.1016/j.neuroimage.2008.03.023](https://doi.org/10.1016/j.neuroimage.2008.03.023)
- Houweling, S., van Dijk, B. W., Beek, P. J., & Daffertshofer, A. (2010). Cortico-spinal synchronization reflects changes in performance when learning a complex bimanual task. *NeuroImage*, *49*, 3269–3275.
- Hummel, F., Kirsammer, R., & Gerloff, C. (2003). Ipsilateral cortical activation during finger sequences of increasing complexity: representation of movement difficulty or memory load? *Clinical Neurophysiology*, *114*, 605–613. [https://doi.org/10.1016/S1388-2457\(02\)00417-0](https://doi.org/10.1016/S1388-2457(02)00417-0)
- Huo, X., Wang, Y., Kotecha, R., Kirtman, E.G., Fujiwara, H., Hemasilpin, N., . . . Xiang, J. (2011). High gamma oscillations of sensorimotor cortex during unilateral movement in the developing brain: A MEG study. *Brain Topography*, *23*, 375–384. [https://doi.org/10.1007/s10](https://doi.org/10.1007/s10548-010-0151-0) [548-010-0151-0](https://doi.org/10.1007/s10548-010-0151-0)
- Igarashi, J., Isomura, Y., Arai, K., Harukuni, R., & Fukai, T. (2013). A θ-γ oscillation code for neuronal coordination during motor behavior. *Journal of Neuroscience*, *33*, 18515–18530.